Cara melakukan regresi logistik di sas

Regresi logistik adalah metode yang dapat kita gunakan untuk menyesuaikan model regresi ketika variabel responnya adalah biner.

Regresi logistik menggunakan metode yang disebut estimasi kemungkinan maksimum untuk mencari persamaan dalam bentuk berikut:

log[p(X) / (1 _– p(X))] = β ₀ + β ₁ X ₁ + β ₂ X ₂ + … + β _p

Emas:

• X _j : variabel prediktif ^ke -j
• β _j : estimasi koefisien variabel prediktif ke- ^j

Rumus di sisi kanan persamaan memprediksi log odds bahwa variabel respons bernilai 1.

Contoh langkah demi langkah berikut menunjukkan cara menyesuaikan model regresi logistik di SAS.

Langkah 1: Buat kumpulan data

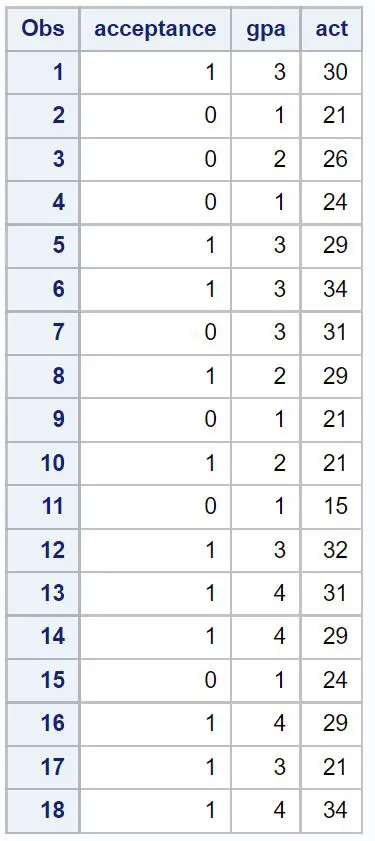
Pertama, kita akan membuat dataset yang berisi informasi tiga variabel berikut untuk 18 siswa:

• Penerimaan ke perguruan tinggi tertentu (1 = ya, 0 = tidak)
• IPK (skala 1 hingga 4)
• Skor ACT (skala 1 hingga 36)

 /*create dataset*/
data my_data;
    input acceptance gpa act;
    datalines ;
1 3 30
0 1 21
0 2 26
0 1 24
1 3 29
1 3 34
0 3 31
1 2 29
0 1 21
1 2 21
0 1 15
1 3 32
1 4 31
1 4 29
0 1 24
1 4 29
1 3 21
1 4 34
;
run ;

/*view dataset*/
proc print data =my_data;

Langkah 2: Sesuaikan model regresi logistik

Selanjutnya, kita akan menggunakan logistik proc agar sesuai dengan model regresi logistik, menggunakan “penerimaan” sebagai variabel respons dan “gpa” dan “tindakan” sebagai variabel prediktor.

Catatan : Penurunan harus ditentukan agar SAS dapat memprediksi probabilitas bahwa variabel respons akan bernilai 1. Secara default, SAS memprediksi probabilitas bahwa variabel respons akan bernilai 0.

 /*fit logistic regression model*/
proc logistic data =my_data descending ;
  model acceptance = gpa act;
run ;

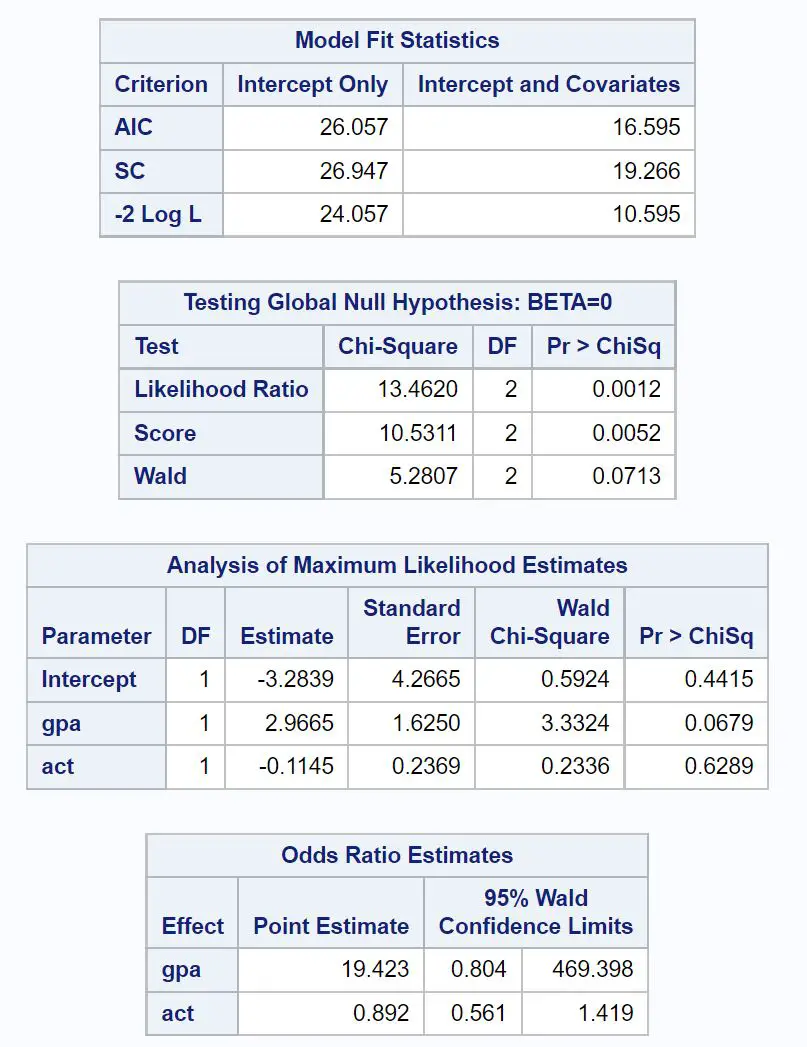
Tabel pertama yang menarik diberi judul Statistik Model Fit .

Dari tabel tersebut kita dapat melihat nilai AIC modelnya yaitu sebesar 16.595 . Semakin rendah nilai AIC maka semakin baik model tersebut mampu fit dengan data.

Namun, tidak ada batasan untuk apa yang dianggap sebagai nilai AIC yang “baik” . Sebaliknya, kami menggunakan AIC untuk membandingkan kesesuaian beberapa model dengan kumpulan data yang sama. Model dengan nilai AIC terendah umumnya dianggap terbaik.

Tabel menarik berikutnya berjudul Menguji Hipotesis Nol Global: BETA=0 .

Dari tabel ini, kita dapat melihat nilai chi-kuadrat rasio kemungkinan sebesar 13,4620 dengan nilai p yang sesuai sebesar 0,0012 .

Karena nilai p ini kurang dari 0,05, hal ini menunjukkan bahwa model regresi logistik secara keseluruhan signifikan secara statistik.

Selanjutnya kita dapat menganalisis estimasi koefisien pada tabel berjudul Analisis Estimasi Kemungkinan Maksimum .

Dari tabel ini kita dapat melihat koefisien IPK dan Act yang menunjukkan rata-rata perubahan log odds diterima masuk perguruan tinggi dengan kenaikan satu satuan pada setiap variabel.

Misalnya:

• Peningkatan nilai IPK sebesar satu unit dikaitkan dengan peningkatan rata-rata sebesar 2,9665 pada log odds untuk diterima di perguruan tinggi.
• Peningkatan skor ACT sebesar satu unit dikaitkan dengan penurunan log odds rata-rata sebesar 0,1145 untuk diterima di perguruan tinggi.

Nilai p yang sesuai pada hasil juga memberi kita gambaran tentang seberapa efektif setiap variabel prediktor dalam memprediksi kemungkinan diterima:

• Nilai P IPK: 0,0679
• Nilai P ACT: 0,6289

Hal ini menunjukkan bahwa IPK tampaknya merupakan prediktor penerimaan perguruan tinggi yang signifikan secara statistik, sedangkan skor ACT tampaknya tidak signifikan secara statistik.

Sumber daya tambahan

Tutorial berikut menjelaskan cara menyesuaikan model regresi lain di SAS:

Cara melakukan regresi linier sederhana di SAS
Cara melakukan regresi linier berganda di SAS