Pengujian hipotesis untuk proporsi

Oleh Agustus 3, 2023 Statistik 0 Komentar

Artikel ini menjelaskan berapa proporsi pengujian hipotesis dalam statistik. Oleh karena itu, Anda akan menemukan rumus uji hipotesis untuk proporsi dan, sebagai tambahan, latihan langkah demi langkah untuk memahami sepenuhnya cara melakukannya.

Apa yang dimaksud dengan pengujian hipotesis untuk proporsi?

Pengujian hipotesis proporsi adalah metode statistik yang digunakan untuk menentukan ditolak atau tidaknya hipotesis nol suatu proporsi populasi.

Jadi, bergantung pada nilai statistik uji hipotesis untuk proporsi dan tingkat signifikansinya, hipotesis nol ditolak atau diterima.

Perhatikan bahwa pengujian hipotesis juga dapat disebut kontras hipotesis, pengujian hipotesis, atau pengujian signifikansi.

Rumus Pengujian Hipotesis Proporsi

Statistik uji hipotesis untuk proporsi sama dengan selisih proporsi sampel dikurangi nilai proporsi yang diusulkan dibagi dengan standar deviasi proporsi.

Oleh karena itu rumus pengujian hipotesis untuk proporsi adalah:

\displaystyle Z=\frac{\widehat{p}-p}{\displaystyle\sqrt{\frac{p(1-p)}{n}}}

Emas:

  • Z

    adalah statistik uji hipotesis untuk proporsi.

  • \widehat{p}

    adalah proporsi sampel.

  • p

    adalah nilai proporsi yang diusulkan.

  • n

    adalah ukuran sampel.

  • \displaystyle\sqrt{\frac{p(1-p)}{n}}

    adalah simpangan baku proporsinya.

Perlu diingat bahwa menghitung statistik uji hipotesis untuk proporsi saja tidak cukup, namun hasilnya harus diinterpretasikan:

  • Jika uji hipotesis untuk proporsi bersifat dua sisi, hipotesis nol ditolak jika nilai absolut statistik lebih besar dari nilai kritis Z α/2 .
  • Jika uji hipotesis untuk proporsi cocok dengan ekor kanan, maka hipotesis nol ditolak jika statistik lebih besar dari nilai kritis Z α .
  • Jika uji hipotesis untuk proporsi cocok dengan ekor kiri, hipotesis nol ditolak jika statistiknya kurang dari nilai kritis -Z α .

\begin{array}{l}H_1: p\neq p_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } |Z|>Z_{\alpha/2} \text{ se rechaza } H_0\\[3ex]H_1: p> p_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } Z>Z_{\alpha} \text{ se rechaza } H_0\\[3ex]H_1: p< p_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } Z<-Z_{\alpha} \text{ se rechaza } H_0\end{array}

Ingatlah bahwa nilai kritis dapat dengan mudah diperoleh dari tabel distribusi normal.

Contoh Pengujian Hipotesis Proporsi

Setelah kita melihat definisi pengujian hipotesis untuk proporsi dan apa rumusnya, kita akan memecahkan contoh untuk memahami konsep dengan lebih baik.

  • Menurut produsennya, obat melawan penyakit tertentu memiliki efektivitas 70%. Di laboratorium, kami menguji efektivitas obat ini karena para peneliti yakin proporsinya berbeda. Untuk itu, obat tersebut diuji pada sampel 1.000 pasien dan 641 orang sembuh. Melakukan uji hipotesis terhadap proporsi populasi dengan tingkat signifikansi 5% untuk menolak atau tidak hipotesis peneliti.

Dalam hal ini hipotesis nol dan hipotesis alternatif uji hipotesis proporsi penduduk adalah:

\begin{cases}H_0: p=0,70\\[2ex] H_1:p\neq 0,70 \end{cases}

Proporsi orang dalam sampel yang sembuh karena obat tersebut adalah:

\widehat{p}=\cfrac{641}{1000}=0,641

Kami menghitung statistik uji hipotesis untuk proporsi dengan menerapkan rumus di atas:

\begin{aligned} \displaystyle Z&=\frac{\widehat{p}-p}{\displaystyle\sqrt{\frac{p(1-p)}{n}}}\\[2ex]Z&=\frac{0,641-0,70}{\displaystyle\sqrt{\frac{0,70\cdot (1-0,70)}{1000}}} \\[2ex] Z&=-4,07\end{aligned}}

Sebaliknya, karena tingkat signifikansinya adalah 0,05 dan ini merupakan uji hipotesis dua sisi, maka nilai kritis uji tersebut adalah 1,96.

Z_{0,025}=1,96

Kesimpulannya, nilai absolut statistik uji lebih besar dari nilai kritis, sehingga hipotesis nol ditolak dan hipotesis alternatif diterima.

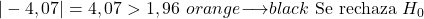|-4,07|=4,07>1,96 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Se rechaza } H_0″ title=”Rendered by QuickLaTeX.com” height=”19″ width=”424″ style=”vertical-align: -5px;”></p> </p> <div style= ➤ Lihat: Pengujian hipotesis untuk mean

Pengujian hipotesis untuk dua proporsi sampel

Pengujian hipotesis proporsi dua sampel digunakan untuk menolak atau menerima hipotesis nol yang menyatakan proporsi dua populasi berbeda adalah sama.

Jadi, hipotesis nol dari uji hipotesis untuk proporsi dua sampel selalu:

H_0: p_1=p_2

Sedangkan hipotesis alternatif dapat berupa salah satu dari tiga pilihan:

 *** QuickLaTeX cannot compile formula:
\begin{array}{l}H_1:p_1\neq p_2\\[2ex]H_1:p_1>p_2\\[2ex]H_1:p_1 The combined ratio of the two samples is calculated as follows:[latex]p=\cfrac {x_1+x_2}{n_1+n_2}

*** Error message:
Missing $ inserted.
leading text: \begin{array}{l}
Please use \mathaccent for accents in math mode.
leading text: ...H_1:p_1>p_2\\[2ex]H_1:p_1 The combined ratio
Please use \mathaccent for accents in math mode.
leading text: ...\[2ex]H_1:p_1 The combined ratio of the two
Please use \mathaccent for accents in math mode.
leading text: ...combined of the two samples is calculated
\begin{array} on input line 8 ended by \end{document}.
leading text: \end{document}
Improper \prevdepth.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
Missing } inserted.
leading text: \end{document}
Missing \cr inserted.
leading text: \end{document}
Missing $ inserted.
leading text: \end{document}
You can't use `\end' in internal vertical mode.

Dan rumus menghitung statistik uji hipotesis untuk dua proporsi sampel adalah:

\displaystyle Z=\frac{\displaystyle \frac{x_1}{n_1}-\frac{x_2}{n_2}}{\displaystyle \sqrt{p(1-p)\left(\frac{1}{n_1}+\frac{1}{n_2}\right)}}

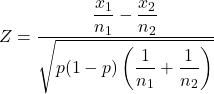
Emas:

  • Z

    adalah statistik uji hipotesis untuk proporsi dua sampel.

  • x_1

    adalah banyaknya hasil pada sampel 1.

  • x_2

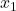
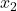
    adalah banyaknya hasil pada sampel 2.

  • n_1

    adalah ukuran sampel 1.

  • n_2

    adalah ukuran sampel 2.

  • p

    adalah proporsi gabungan dari dua sampel.

Pengujian hipotesis untuk k proporsi sampel

Dalam uji hipotesis tentang proporsi k sampel, tujuannya adalah untuk menentukan apakah semua proporsi populasi yang berbeda adalah sama atau sebaliknya, apakah terdapat proporsi yang berbeda. Oleh karena itu, hipotesis nol dan hipotesis alternatif dalam hal ini adalah:

\begin{cases}H_0: \text{Todas las proporciones son iguales}\\[2ex] H_1: \text{No todas las proporciones son iguales} \end{cases}

Dalam hal ini, proporsi gabungan seluruh sampel dihitung sebagai berikut:

p=\cfrac{\displaystyle\sum_{i=1}^k x_i}{\displaystyle\sum_{i=1}^k n_i}=\cfrac{x_1+x_2+\dots+x_k}{n_1+n_2+\dots+n_k}

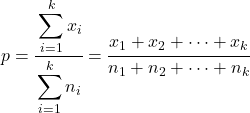
Rumus mencari statistik uji hipotesis untuk k proporsi sampel adalah:

\displaystyle \chi^2 =\sum_{i=1}^k \frac{(x_i-e_i)^2}{e_i}

\displaystyle\chi^2 = \frac{(x_1-e_1)^2}{e_1} +\frac{(x_2-e_2)^2}{e_2} +\dots+\frac{(x_k-e_k)^2}{e_k}

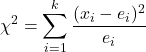
Emas:

  • \chi^2

    adalah statistik uji hipotesis untuk k proporsi sampel. Dalam hal ini statistik mengikuti distribusi chi-kuadrat.

  • x_i

    adalah banyaknya hasil pada sampel i.

  • n_i

    adalah ukuran sampel i.

  • p

    adalah proporsi gabungan dari semua sampel.

  • e_i

    adalah jumlah hit yang diharapkan dari sampel i. Hal ini dihitung dengan mengalikan proporsi gabungan

    p

    berdasarkan ukuran sampel

    n_i

    .

Tentang Penulis

Benjamin Anderson
Benjamin anderson

Halo, saya Benjamin, pensiunan profesor statistika yang menjadi guru Statorial yang berdedikasi. Dengan pengalaman dan keahlian yang luas di bidang statistika, saya ingin berbagi ilmu untuk memberdayakan mahasiswa melalui Statorials. Baca selengkapnya

Tambahkan komentar

Alamat email Anda tidak akan dipublikasikan. Ruas yang wajib ditandai *