Distribusi pengambilan sampel mean
Artikel ini menjelaskan apa itu distribusi sampling mean dalam statistik. Anda juga akan menemukan rumus distribusi pengambilan sampel rata-rata dan latihan penyelesaian langkah demi langkah.
Berapakah distribusi sampling meannya?
Distribusi rata-rata pengambilan sampel (atau distribusi rata-rata pengambilan sampel ) adalah distribusi yang dihasilkan dari penghitungan rata-rata pengambilan sampel dari setiap kemungkinan sampel dari suatu populasi. Artinya, himpunan mean sampel dari semua sampel yang mungkin dari suatu populasi membentuk distribusi sampling dari mean tersebut.
Atau dengan kata lain, jika kita mempelajari semua sampel yang dapat diambil dari suatu populasi dan menghitung rata-rata masing-masing sampel, maka himpunan nilai yang dihitung tersebut membentuk distribusi sampling dari mean sampel.
Dalam statistik, distribusi sampling dari mean digunakan untuk menghitung probabilitas mendekati nilai mean populasi ketika menganalisis sampel tunggal.
Rumus distribusi sampling mean
Diberikan populasi yang mengikuti distribusi probabilitas normal dengan mean
![]()
dan deviasi standar
![]()
dan ukuran sampel diekstraksi
![]()
, distribusi sampling mean juga akan ditentukan oleh distribusi normal yang memiliki ciri-ciri sebagai berikut:
![Rendered by QuickLaTeX.com \begin{array}{c}\mu_{\overline{x}}=\mu \qquad \sigma_{\overline{x}}=\cfrac{\sigma}{\sqrt{n}}\\[4ex]\displaystyle N_{\overline{x}}\left(\mu, \frac{\sigma}{\sqrt{n}}\right) \end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-44571aa7337b095ab9c9fa1f746e93a5_l3.png)
Emas
![]()
adalah mean dari distribusi sampling dari mean dan
![]()
adalah deviasi standarnya. Lebih-lebih lagi,
![]()
adalah kesalahan standar distribusi sampling.
Catatan: Jika populasi tidak mengikuti distribusi normal tetapi ukuran sampelnya besar (n>30), distribusi sampling mean juga dapat didekati dengan distribusi normal sebelumnya dengan teorema limit pusat.
Oleh karena itu, karena distribusi sampling dari mean mengikuti distribusi normal, rumus untuk menghitung probabilitas apa pun yang terkait dengan mean sampel adalah:

Emas:
-

adalah sarana sampel.
-

Ini adalah rata-rata populasi.
-

adalah simpangan baku populasi.
-

adalah ukuran sampel.
-

adalah variabel yang ditentukan oleh distribusi normal standar N(0,1).
Contoh nyata distribusi sampling mean
Setelah melihat definisi distribusi sampling mean dan rumus terkaitnya, mari kita selesaikan sebuah contoh untuk memahami konsepnya dengan lebih baik.
- Berat badan mahasiswa mengikuti distribusi normal dengan rata-rata 68 kg dan simpangan baku 9 kg. Bertekad:
- Berapa peluang rata-rata sampel acak yang terdiri dari 25 siswa memiliki berat badan kurang dari 66 kg?
- Jika diambil 300 sampel yang masing-masing berjumlah 25 siswa, berapakah rata-rata sampel yang nilainya kurang dari 66 kg?
Pertama-tama, kita harus menghitung nilai statistik yang bersangkutan, untuk ini kita menerapkan rumus yang kita lihat di atas:
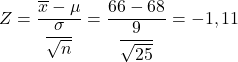
Oleh karena itu, probabilitas yang kita cari adalah yang sesuai dengan nilai Z=-1,11 di ekor kiri distribusi normal standar, yang dapat dengan mudah diperoleh dari tabel probabilitas Z. Oleh karena itu kami menggunakan tabel Z untuk menentukan probabilitas bahwa masalah tersebut menanyakan kepada kami:
![]()
Sekarang kita mengetahui probabilitas bahwa rata-rata sampel acak kurang dari 66 kg, untuk mengetahui jumlah rata-rata sampel kurang dari 66 kg dengan mengambil 300 sampel yang sama, kita perlu mengalikan probabilitas yang dihitung dengan jumlah total sampel yang diambil:
![]()
Oleh karena itu, sekitar 40 sampel yang diekstraksi memiliki rata-rata kurang dari 66 kg.