Distribusi pengambilan sampel perbedaan rata-rata
Artikel ini menjelaskan apa itu distribusi sampling dari perbedaan antara dua mean dalam statistik. Anda juga akan menemukan rumus untuk distribusi sampling dari selisih rata-rata dan, sebagai tambahan, latihan penyelesaian langkah demi langkah.
Berapakah distribusi sampling dari perbedaan rata-rata?
Distribusi sampling selisih mean adalah distribusi yang dihasilkan dari penghitungan selisih mean seluruh kemungkinan sampel dari dua populasi yang berbeda.
Artinya, untuk memperoleh distribusi sampling dari selisih mean, semua sampel yang mungkin dari dua populasi penelitian harus dipilih, kemudian dihitung mean dari setiap sampel yang dipilih, dan terakhir, selisih antara semua mean dihitung dari kedua populasi. Dengan demikian, himpunan nilai yang diperoleh setelah penerapan semua operasi ini membentuk distribusi sampling dari selisih rata-rata.

Perbedaan distribusi mean sampling digunakan untuk menghitung probabilitas bahwa perbedaan antara dua mean sampel yang dipilih secara acak dari dua populasi berbeda mendekati perbedaan mean populasi.
Rumus distribusi sampling selisih mean
Jika ukuran sampel cukup besar (n 1 ≥30 dan n 2 ≥30), distribusi sampling selisih mean mengikuti distribusi normal. Lebih tepatnya parameter distribusi tersebut dihitung sebagai berikut:
![Rendered by QuickLaTeX.com \begin{array}{c}\displaystyle \mu_{\overline{x_1}-\overline{x_2}}=\mu_1-\mu_2 \qquad \sigma_{\overline{x_1}-\overline{x_2}}=\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\\[6ex]\displaystyle N_{\overline{x_1}-\overline{x_2}}\left(\mu_1-\mu_2, \sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\right) \end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-90c67b74b4e9326b7869d641a59725d9_l3.png)
Catatan: Jika kedua populasi berdistribusi normal , maka distribusi sampling dari selisih rata-rata mengikuti distribusi normal tanpa memandang ukuran sampel.
Oleh karena itu, karena distribusi sampling selisih mean ditentukan oleh distribusi normal, maka rumus untuk menghitung statistik distribusi sampling selisih mean adalah:

Emas:
-

adalah rata-rata sampel i.
-

adalah rata-rata populasi i.
-

adalah simpangan baku populasi i.
-

adalah ukuran sampel i.
-

adalah variabel yang ditentukan oleh distribusi normal standar N(0,1).
Perhatikan bahwa sampel dari populasi yang berbeda mungkin memiliki ukuran sampel yang berbeda.
Contoh konkrit distribusi sampling selisih mean
Setelah kita melihat pengertian distribusi mean sampling dan apa rumusnya, kita akan melihat contoh langkah demi langkah untuk menyelesaikan pemahaman konsep distribusi mean sampling.
- Dalam sebuah studi statistik, kami ingin menganalisis perbedaan antara tinggi badan anak laki-laki dan perempuan pada usia tertentu. Kita mengetahui bahwa distribusi yang menentukan jumlah penduduk laki-laki pada usia tersebut mempunyai rata-rata 157 cm dan simpangan baku 9 cm, sedangkan distribusi yang menentukan jumlah penduduk anak perempuan pada usia tersebut mempunyai rata-rata 148. cm dan simpangan baku 7 cm. Jika diambil sampel 30 anak laki-laki pada usia tersebut dan sampel 35 anak perempuan pada usia tersebut, berapa peluang rata-rata tinggi badan sampel anak laki-laki lebih besar 12 cm dibandingkan rata-rata tinggi badan sampel anak perempuan?
Untuk mengatasi masalah ini, hal pertama yang harus dilakukan adalah menghitung statistik selisih distribusi mean sampling. Oleh karena itu kami menerapkan rumus yang terlihat di atas:
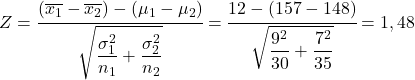
Oleh karena itu, peluang rata-rata tinggi sampel anak laki-laki lebih besar 12 cm dari rata-rata tinggi badan anak perempuan setara dengan peluang variabel Z lebih besar dari 1,48.
![P[(\overline{x_1}-\overline{x_2})>12]=P[Z>1,48]” title=”Rendered by QuickLaTeX.com” height=”19″ width=”253″ style=”vertical-align: -5px;”></p>
</p>
<p> Oleh karena itu kami mencari probabilitas Z>1,48 pada <a href=](https://statorials.org/wp-content/ql-cache/quicklatex.com-683cd2a72980115d8d18c906d619370a_l3.png) tabel Z :
tabel Z :
![P[(\overline{x_1}-\overline{x_2})>12]=P[Z>1,48]=0,0694″ title=”Rendered by QuickLaTeX.com” height=”19″ width=”331″ style=”vertical-align: -5px;”></p>
</p>
<p> Singkatnya, peluang rata-rata tinggi sampel anak laki-laki lebih besar 12 cm dibandingkan rata-rata tinggi badan anak perempuan adalah 6,94%.</p>
</div><!-- End Content -->
<!-- Start Author Box -->
<div class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-5b83fdc11bd2320249679c4752660451_l3.png)
Tentang Penulis
Benjamin anderson
Halo, saya Benjamin, pensiunan profesor statistika yang menjadi guru Statorial yang berdedikasi. Dengan pengalaman dan keahlian yang luas di bidang statistika, saya ingin berbagi ilmu untuk memberdayakan mahasiswa melalui Statorials. Baca selengkapnya