Interval kepercayaan untuk perbedaan rata-rata
Artikel ini menjelaskan apa itu interval kepercayaan untuk perbedaan rata-rata dalam statistik dan kegunaannya. Jadi, Anda akan menemukan cara menghitung interval kepercayaan untuk selisih dua mean dan latihan yang diselesaikan langkah demi langkah.
Berapakah selang kepercayaan untuk selisih rata-rata?
Interval kepercayaan selisih mean adalah suatu interval yang memberikan nilai maksimum dan nilai minimum dimana antara nilai selisih mean dua populasi terletak pada tingkat kepercayaan tertentu.
Misalnya, jika selang kepercayaan selisih mean dua populasi dengan tingkat kepercayaan 95% adalah (3,5), berarti selisih mean kedua populasi tersebut adalah antara 3 dan 5 dengan probabilitas 95. %.
Oleh karena itu, dalam statistik, selang kepercayaan untuk perbedaan rata-rata digunakan untuk memperkirakan dua nilai di mana letak perbedaan antara dua rata-rata populasi. Jadi, dengan menggunakan data dari dua sampel, perbedaan antara rata-rata populasi dapat diperkirakan.
Rumus interval kepercayaan untuk selisih mean
Rumus selang kepercayaan untuk selisih mean bergantung pada diketahui atau tidaknya varians populasi dan, jika tidak, dapat diasumsikan sama atau tidaknya varians populasi. . Kita kemudian akan melihat bagaimana interval kepercayaan untuk selisih mean dihitung dalam setiap kasus.
penyimpangan yang diketahui
Rumus untuk menghitung selang kepercayaan selisih mean bila diketahui varians kedua populasi dengan tingkat kepercayaan 1-α adalah sebagai berikut:
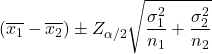
Emas:
-

adalah rata-rata sampel i.
-

adalah simpangan baku populasi i.
-

adalah nilai distribusi normal standar dengan probabilitas α/2.
-

adalah ukuran sampel i.
Kasus ini merupakan kasus yang paling jarang terjadi, karena nilai varians populasi umumnya tidak diketahui.
varians yang tidak diketahui dan sama
Apabila varians kedua populasi tidak diketahui tetapi dapat diperkirakan sama, maka rumus menghitung selang kepercayaan selisih mean dengan tingkat kepercayaan 1-α adalah sebagai berikut:
![]()
Emas:
-

adalah rata-rata sampel i.
-

adalah deviasi standar gabungan.
-

adalah nilai distribusi t Student n 1 + n 2 -2 derajat kebebasan dengan probabilitas α/2.
-

adalah ukuran sampel i.
Karena dalam hal ini varians populasi diasumsikan ekuivalen, maka simpangan baku gabungan digunakan untuk menghitung selang kepercayaan, yang dihitung dengan rumus berikut:

Emas
![]()
adalah simpangan baku sampel i.
Variasi yang tidak diketahui dan berbeda
Apabila varians kedua populasi tidak diketahui dan tidak dapat dianggap sama, maka rumus menghitung selang kepercayaan selisih mean dengan tingkat kepercayaan 1-α adalah sebagai berikut:
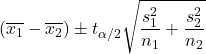
Emas:
-

adalah rata-rata sampel i.
-
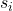
adalah simpangan baku sampel i.
-

adalah nilai distribusi t Student dengan probabilitas α/2.
-

adalah ukuran sampel i.
Dalam hal ini derajat kebebasan distribusi t Student dihitung dengan menggunakan rumus berikut:

Emas
![]()
adalah simpangan baku sampel i.
Contoh konkrit selang kepercayaan untuk selisih rata-rata
Setelah melihat definisi selang kepercayaan untuk selisih rata-rata dan apa saja rumus-rumus yang berbeda, sekarang kita akan melihat contoh konkrit untuk menyelesaikan asimilasi bagaimana selang kepercayaan untuk selisih dua rata-rata dihitung.
- Kami ingin mempelajari pengaruh tembakau terhadap berat lahir anak. Untuk melakukan hal ini, dua sampel dibandingkan: sampel pertama terdiri dari anak-anak yang ibunya tidak merokok dan sampel kedua terdiri dari anak-anak yang ibunya merokok (parameter sampel ditunjukkan di bawah). Hitung selang kepercayaan selisih mean dengan tingkat kepercayaan 95%.
- Ibu yang tidak merokok:
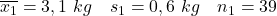
- Ibu perokok:
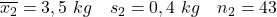
- Ibu yang tidak merokok:
Dalam hal ini kita tidak mengetahui nilai varians populasinya, namun kita dapat berasumsi bahwa varians populasi tersebut ekuivalen karena kita berhadapan dengan dua populasi yang mempunyai karakteristik yang sangat mirip. Oleh karena itu, rumus selang kepercayaan selisih rata-rata yang sebaiknya kita gunakan adalah:
![]()
Jadi, kami menghitung simpangan baku gabungan dari simpangan baku kedua sampel:
![Rendered by QuickLaTeX.com \begin{aligned}\displaystyle s_p&=\sqrt{\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}}\\[2ex]\displaystyle s_p&=\sqrt{\frac{(39-1)\cdot 0,6^2+(43-1)\cdot 0,4^2}{39+43-2}}\\[2ex]\displaystyle s_p&=0,50\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-688958252e9838e7fddc2ddcb9061b01_l3.png)
Demikian pula kita harus mencari nilai distribusi t Student 80 derajat kebebasan dengan probabilitas 2,5% pada tabel distribusi probabilitas distribusi t Student :
![]()
![Rendered by QuickLaTeX.com \begin{array}{c}t_{\alpha/2| n_1+n_2-2}= \ \color{orange}\bm{?}\\[4ex]t_{0,025|80}=1,990\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-5e4ea90fdc33c9a3d3dab0f1d9d29af0_l3.png)
Terakhir, kami mengganti data ke dalam rumus interval kepercayaan untuk selisih rata-rata dan melakukan perhitungan:
![]()
![]()
![]()
Oleh karena itu, selang kepercayaan untuk perbedaan cara menyelesaikan soal adalah sebagai berikut:
![]()