Distribusi pengambilan sampel

Oleh Benjamin anderson Agustus 3, 2023 Statistik 0 Komentar

Artikel ini menjelaskan apa itu distribusi sampling dalam statistik dan kegunaannya. Jadi, Anda akan menemukan pengertian distribusi sampling, contoh konkrit dari distribusi sampling, dan selain itu juga rumus-rumus jenis distribusi sampling yang paling umum.

Bagaimana distribusi samplingnya?

Distribusi sampling , atau distribusi sampling , adalah distribusi yang dihasilkan dari mempertimbangkan semua kemungkinan sampel dari suatu populasi. Dengan kata lain, distribusi sampling adalah distribusi yang diperoleh dengan menghitung parameter sampling dari seluruh kemungkinan sampel dari suatu populasi.

Misalnya, jika kita mengekstrak semua sampel yang mungkin dari suatu populasi statistik dan menghitung rata-rata setiap sampel, himpunan rata-rata sampel membentuk distribusi pengambilan sampel. Lebih tepatnya, karena parameter yang dihitung adalah mean aritmatika, maka ini adalah distribusi sampling dari mean.

Dalam statistik, distribusi sampling digunakan untuk menghitung probabilitas mendekati nilai parameter populasi ketika mempelajari suatu sampel. Demikian pula, distribusi pengambilan sampel memungkinkan kita memperkirakan kesalahan pengambilan sampel untuk ukuran sampel tertentu.

Contoh Distribusi Sampling

Sekarang setelah kita mengetahui definisi distribusi sampling, mari kita lihat contoh sederhana untuk memahami konsep tersebut sepenuhnya.

Dalam sebuah kotak kita masukkan tiga bola dan masing-masing bola dituliskan angka satu sampai tiga, sehingga bola yang satu bernomor 1, bola yang lain bernomor 2, dan bola terakhir bernomor 3. Untuk sampel berukuran n = 2, menghitung probabilitas distribusi sampling dari mean jika sampel dengan penggantian dipilih.

Sampel dipilih dengan penggantian, yaitu bola yang diambil untuk memilih elemen pertama sampel dikembalikan ke kotak dan dapat dipilih kembali pada ekstraksi kedua. Oleh karena itu, semua sampel yang mungkin dari populasi adalah:

1.1 1.2 1.3
2.1 2.2 2.3
3.1 3.2 3.3

Jadi, kami menghitung mean aritmatika dari setiap sampel yang mungkin:

$(1,1) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{11}=\cfrac{1+1}{2}=1$

$(1,2) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{12}=\cfrac{1+2}{2}=1,5$

$(1,3) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{13}=\cfrac{1+3}{2}=2$

$(2,1) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{21}=\cfrac{2+1}{2}=1,5$

$(2,2) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{22}=\cfrac{2+2}{2}=2$

$(2,3) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{23}=\cfrac{2+3}{2}=2,5$

$(3,1) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{31}=\cfrac{3+1}{2}=2$

$(3,2) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{32}=\cfrac{3+2}{2}=2,5$

$(3,3) \ \color{orange}\bm{\longrightarrow}\color{black} \ \overline{x}_{33}=\cfrac{3+3}{2}=3$

Oleh karena itu, peluang diperolehnya setiap nilai mean sampel ketika memilih sampel acak dari populasi adalah sebagai berikut:

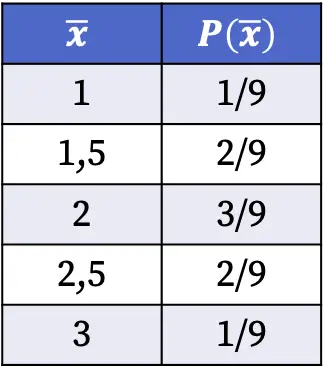
Probabilitas distribusi pengambilan sampel yang ditunjukkan pada tabel di atas dihitung dengan membagi jumlah sampel yang memiliki nilai rata-rata tersebut dengan jumlah total kemungkinan kasus. Misalnya: mean sampel adalah 1,5 dalam dua kasus dari sembilan kemungkinan, oleh karena itu P(1,5)=2/9.

Jenis distribusi pengambilan sampel

Distribusi pengambilan sampel (atau distribusi pengambilan sampel) dapat diklasifikasikan berdasarkan parameter pengambilan sampel dari mana distribusi tersebut diperoleh. Jadi, jenis distribusi yang paling umum adalah sebagai berikut:

Distribusi rata-rata pengambilan sampel : Ini adalah distribusi pengambilan sampel yang dihasilkan dari penghitungan rata-rata aritmatika setiap sampel.
Distribusi Proporsi Sampling : Merupakan distribusi sampling yang diperoleh dengan menghitung proporsi seluruh sampel.
Distribusi varians sampling : Ini adalah distribusi sampling yang membentuk himpunan semua varians dalam sampel.
Perbedaan distribusi mean sampling : adalah distribusi sampling yang dihasilkan dari penghitungan selisih mean seluruh sampel yang mungkin dari dua populasi yang berbeda.
Perbedaan Distribusi Proporsi Sampling : adalah distribusi sampling yang diperoleh dengan mengurangkan semua kemungkinan proporsi sampling dari dua populasi.

Setiap jenis distribusi sampling dijelaskan lebih rinci di bawah ini.

Distribusi pengambilan sampel mean

Diberikan populasi yang mengikuti distribusi probabilitas normal dengan mean

$\mu$

dan deviasi standar

$\sigma$

dan ukuran sampel diekstraksi

$n$

, distribusi sampling mean juga akan ditentukan oleh distribusi normal yang memiliki ciri-ciri sebagai berikut:

$\begin{array}{c}\mu_{\overline{x}}=\mu \qquad \sigma_{\overline{x}}=\cfrac{\sigma}{\sqrt{n}}\\[4ex]\displaystyle N_{\overline{x}}\left(\mu, \frac{\sigma}{\sqrt{n}}\right) \end{array}$

Emas

$\mu_{\overline{x}}$

adalah mean dari distribusi sampling dari mean dan

$\sigma_{\overline{x}}$

adalah deviasi standarnya. Lebih-lebih lagi,

$\cfrac{\sigma}{\sqrt{n}}$

adalah kesalahan standar distribusi sampling.

Catatan: Jika populasi tidak mengikuti distribusi normal tetapi ukuran sampelnya besar (n>30), distribusi sampling dari mean juga dapat didekati dengan distribusi normal di atas dengan batas teorema pusat.

Oleh karena itu, karena distribusi sampling dari mean mengikuti distribusi normal, rumus untuk menghitung probabilitas apa pun yang terkait dengan mean sampel adalah:

$Z=\cfrac{\overline{x}-\mu}{\displaystyle\frac{\sigma}{\sqrt{n}}}$

Emas:

$\overline{x}$

adalah sarana sampel.
$\mu$

Ini adalah rata-rata populasi.
$s$

adalah simpangan baku populasi.
$n$

adalah ukuran sampel.
$Z$

adalah variabel yang ditentukan oleh distribusi normal standar N(0,1).

➤ Lihat: Latihan soal distribusi sampling mean

Distribusi proporsi sampel

Faktanya, ketika kami mempelajari suatu proporsi sampel, kami menganalisis kasus-kasus keberhasilan. Oleh karena itu, variabel acak dalam penelitian mengikuti distribusi probabilitas binomial.

Menurut teorema limit pusat, untuk ukuran besar (n>30) kita dapat mendekatkan distribusi binomial ke distribusi normal. Oleh karena itu, distribusi sampling proporsinya mendekati distribusi normal dengan parameter berikut:

$\begin{array}{c}\displaystyle\mu_{p}=p \qquad \sigma_{p}=\sqrt{\frac{pq}{n}}\\[4ex]\displaystyle N_{p}\left(p, \sqrt{\frac{pq}{n}}\right) \end{array}$

Emas

$p$

adalah kemungkinan sukses dan

$q$

adalah kemungkinan kegagalan

$q=1-p$

Catatan: Distribusi binomial hanya dapat didekati dengan distribusi normal jika

$n>30″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”52″ style=”vertical-align: -2px;”></p> <p> ,</p> <p class=$ $np\ge 5$

Dan

$nq\ge 5$

Oleh karena itu, karena distribusi sampling dari suatu proporsi dapat didekati dengan distribusi normal, maka rumus untuk menghitung probabilitas apa pun yang berkaitan dengan proporsi suatu sampel adalah:

$Z=\cfrac{\widehat{p}-p}{\displaystyle\sqrt{\frac{pq}{n}}}$

Emas:

$\widehat{p}$

adalah proporsi sampel.
$p$

adalah proporsi penduduk.
$q$

adalah probabilitas kegagalan populasi,

$q=1-p$

.
$n$

adalah ukuran sampel.
$Z$

adalah variabel yang ditentukan oleh distribusi normal standar N(0,1).

➤ Lihat: Latihan soal distribusi sampling proporsi

Distribusi Varians Pengambilan Sampel

Distribusi varians pengambilan sampel ditentukan oleh distribusi probabilitas chi-kuadrat. Oleh karena itu, rumus statistik distribusi varians sampling adalah:

$\chi^2=\cfrac{(n-1)s^2}{\sigma^2}$

Emas:

$\chi^2$

adalah statistik dari distribusi varians sampling, yang mengikuti distribusi chi-kuadrat.
$n$

adalah ukuran sampel.
$s^2$

adalah varians sampel.
$\sigma^2$

adalah varians populasi.

➤ Lihat: Latihan soal distribusi sampling varians

Distribusi pengambilan sampel perbedaan rata-rata

Jika ukuran sampel cukup besar (n ₁ ≥30 dan n ₂ ≥30), distribusi sampling dari perbedaan rata-rata mengikuti distribusi normal. Lebih tepatnya parameter distribusi tersebut dihitung sebagai berikut:

$\begin{array}{c}\displaystyle \mu_{\overline{x_1}-\overline{x_2}}=\mu_1-\mu_2 \qquad \sigma_{\overline{x_1}-\overline{x_2}}=\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\\[6ex]\displaystyle N_{\overline{x_1}-\overline{x_2}}\left(\mu_1-\mu_2, \sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\right) \end{array}$

Catatan: Jika kedua populasi berdistribusi normal, maka distribusi sampling dari selisih rata-rata mengikuti distribusi normal tanpa memandang ukuran sampel.

Oleh karena itu, karena distribusi sampling selisih mean ditentukan oleh distribusi normal, maka rumus untuk menghitung statistik distribusi sampling selisih mean adalah:

$Z=\cfrac{(\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}}$

Emas:

$\overline{x_i}$

adalah rata-rata sampel i.
$\mu_i$

adalah rata-rata populasi i.
$\sigma_i$

adalah simpangan baku populasi i.
$n_i$

adalah ukuran sampel i.
$Z$

adalah variabel yang ditentukan oleh distribusi normal standar N(0,1).

Perhatikan bahwa sampel dari populasi yang berbeda mungkin memiliki ukuran sampel yang berbeda.

➤ Lihat: Latihan soal distribusi sampling dari perbedaan rata-rata

Distribusi sampling perbedaan proporsi

Sampel yang dipilih berdasarkan perbedaan proporsi distribusi pengambilan sampel ditentukan oleh distribusi binomial, karena untuk tujuan praktis proporsi adalah rasio kasus yang berhasil terhadap jumlah total observasi.

Namun, karena teorema limit pusat, distribusi binomial dapat didekati dengan distribusi probabilitas normal. Oleh karena itu, distribusi sampling selisih proporsinya dapat didekati dengan distribusi normal dengan ciri-ciri sebagai berikut:

$\begin{array}{c}\displaystyle\mu_{\widehat{p_1}-\widehat{p_2}}=p_1-p_2 \qquad \sigma_{\widehat{p_1}-\widehat{p_2}}=\sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}\\[6ex]\displaystyle N_{p}\left(p_1-p_2, \sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}\right) \end{array}$

Catatan: Distribusi sampling dari perbedaan proporsi hanya dapat didekati dengan distribusi normal jika

$n_1\geq30$

$n_2\geq 30$

$n_1p_1\geq5$

$n_2p_2\geq5$

$n_1q_1\geq5$

Dan

$n_2q_2\geq5$

Oleh karena itu, karena distribusi sampling selisih proporsi dapat didekati dengan distribusi normal, maka rumus menghitung statistik distribusi sampling selisih proporsi adalah sebagai berikut:

$Z=\cfrac{(\widehat{p_1}-\widehat{p_2})-(p_1-p_2)}{\displaystyle\sqrt{\frac{p_1q_1}{n_1}+\frac{p_2q_2}{n_2}}}$

Emas:

$\widehat{p_i}$

adalah proporsi sampel i.
$p_i$

adalah proporsi penduduk i.
$q_i$

adalah probabilitas kegagalan populasi i,

$q_i=1-p_i$

.
$n_i$

adalah ukuran sampel i.
$Z$

adalah variabel yang ditentukan oleh distribusi normal standar N(0,1).

➤ Lihat: Latihan soal distribusi sampling dari perbedaan proporsi

Tentang Penulis

Benjamin anderson

Halo, saya Benjamin, pensiunan profesor statistika yang menjadi guru Statorial yang berdedikasi. Dengan pengalaman dan keahlian yang luas di bidang statistika, saya ingin berbagi ilmu untuk memberdayakan mahasiswa melalui Statorials. Baca selengkapnya

Bagaimana distribusi samplingnya?

Contoh Distribusi Sampling

Jenis distribusi pengambilan sampel

Distribusi pengambilan sampel mean

Distribusi proporsi sampel

Distribusi Varians Pengambilan Sampel

Distribusi pengambilan sampel perbedaan rata-rata

Distribusi sampling perbedaan proporsi

Tentang Penulis

Benjamin anderson

Tambahkan komentar