Bagaimana menafsirkan standar deviasi nol

Dalam statistik, standar deviasi digunakan untuk mengukur distribusi nilai dalam suatu sampel.

Kita dapat menggunakan rumus berikut untuk menghitung deviasi standar sampel tertentu:

√ Σ( _xi – x _batang ) ² / (n-1)

Emas:

• Σ: Simbol yang berarti “jumlah”
• x _i : nilai ^ke-i dari sampel
• x _bar : Arti sampel
• n: Ukuran sampel

Semakin tinggi nilai standar deviasi, maka semakin tersebar nilai-nilai tersebut dalam suatu sampel .

Semakin rendah nilai standar deviasi, semakin erat pengelompokan nilai-nilai tersebut.

Jika simpangan baku suatu sampel adalah nol, berarti semua nilai dalam sampel tersebut sama persis.

Dengan kata lain, tidak ada kesenjangan antar nilai.

Contoh berikut menunjukkan bagaimana menafsirkan standar deviasi nol dalam praktiknya.

Contoh: Bagaimana menafsirkan standar deviasi nol

Misalkan kita mengumpulkan sampel acak sederhana yang terdiri dari 10 kadal dan mengukur panjangnya (dalam inci):

Panjang : 7, 7, 7, 7, 7, 7, 7, 7, 7, 7

Rata-rata panjang kadal dalam sampel adalah 7 inci.

Mengetahui hal ini, kita dapat menghitung standar deviasi sampel untuk kumpulan data ini:

• s = √ Σ( _xi – x _batang ) ² / (n-1)
• s = √ ((7 – 7) ² + (7 – 7) ² + (7 – 7) ² + … + (7 – 7) ² / (10-1)
• s = √ 0 ² + 0 ² + 0 ² + … + 0 ² / 9
• s = 0

Deviasi standar sampel ternyata 0 .

Karena setiap kadal memiliki panjang yang sama persis, distribusi nilai dalam kumpulan data sama persis dengan nol.

Akankah standar deviasi menjadi nol di dunia nyata?

Sangat mungkin kumpulan data dunia nyata memiliki standar deviasi nol, tetapi hal ini jarang terjadi.

Skenario yang paling mungkin di mana Anda mungkin menghadapi deviasi standar nol adalah saat mengumpulkan sampel kecil untuk kejadian langka.

Misalnya, Anda mengumpulkan data jumlah kecelakaan di jalan raya selama periode satu minggu di kota tertentu.

Sangat mungkin Anda mengumpulkan data berikut:

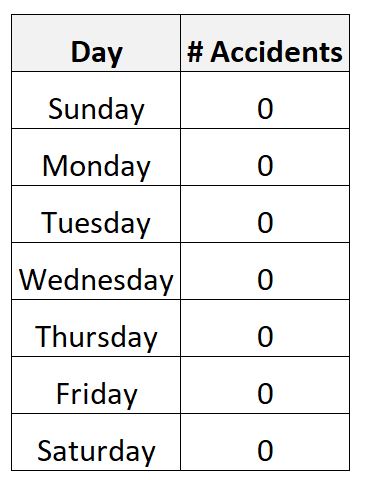
Dalam skenario ini, jumlah rata-rata kecelakaan harian akan menjadi nol dan standar deviasinya juga akan menjadi nol.

Atau mungkin Anda mengumpulkan data berikut tentang jumlah penjualan bulanan suatu produk mahal untuk sebuah bisnis selama periode 6 bulan:

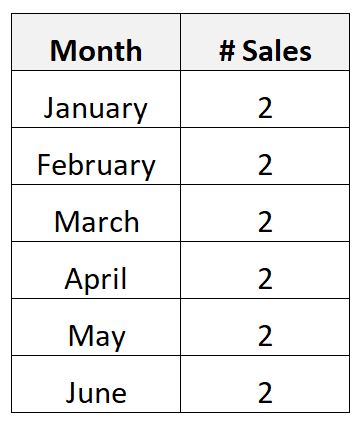
Karena mahalnya produk tersebut, ternyata perusahaan hanya menjual tepat dua buah dalam sebulan.

Dalam skenario ini, jumlah rata-rata produk bulanan yang terjual adalah dua dan standar deviasi produk bulanan yang terjual adalah nol.

Setiap kali Anda menemukan deviasi standar nol dalam kumpulan data nyata, ketahuilah bahwa itu berarti setiap nilai dalam kumpulan data tersebut sama persis.

Sumber daya tambahan

Tutorial berikut memberikan informasi tambahan tentang deviasi standar dalam statistik:

Mengapa deviasi standar penting?
Standar deviasi dan kesalahan standar: apa bedanya?
Deviasi standar dan rentang interkuartil: apa bedanya?