Cara melakukan uji-t dengan ukuran sampel yang tidak sama

Pertanyaan yang sering ditanyakan siswa mengenai statistika adalah:

Apakah mungkin melakukan uji-t ketika ukuran sampel tiap kelompok tidak sama?

Jawaban singkatnya:

Ya, Anda dapat melakukan uji-t jika ukuran sampel tidak sama. Ukuran sampel yang sama bukanlah salah satu asumsi yang dibuat dalam uji-t.

Masalah sebenarnya muncul ketika kedua sampel tidak memiliki varian yang sama, yang merupakan salah satu asumsi yang dibuat dalam uji-t.

Jika hal ini terjadi, disarankan untuk menggunakan uji-t Welch , yang tidak mengasumsikan variansi yang sama.

Contoh berikut menunjukkan cara melakukan uji T dengan ukuran sampel yang tidak sama ketika variansnya sama dan ketika variansnya tidak sama.

Contoh 1: Ukuran sampel yang tidak sama dan varians yang sama

Misalkan kita mengelola dua program yang dirancang untuk membantu siswa berprestasi lebih baik pada ujian tertentu.

Hasilnya adalah sebagai berikut:

Program 1:

• n (ukuran sampel): 500
• x (rata-rata sampel): 80
• s (deviasi standar sampel): 5

Program 2:

• n (ukuran sampel): 20
• x (rata-rata sampel): 85
• s (deviasi standar sampel): 5

Kode berikut menunjukkan cara membuat boxplot di R untuk memvisualisasikan distribusi nilai ujian untuk setiap program:

 #make this example reproducible
set. seeds (1)

#create vectors to hold exam scores
program1 <- rnorm(500, mean=80, sd=5)
program2 <- rnorm(20, mean=85, sd=5)

#create boxplots to visualize distribution of exam scores
boxplot(program1, program2, names=c(" Program 1 "," Program 2 "))

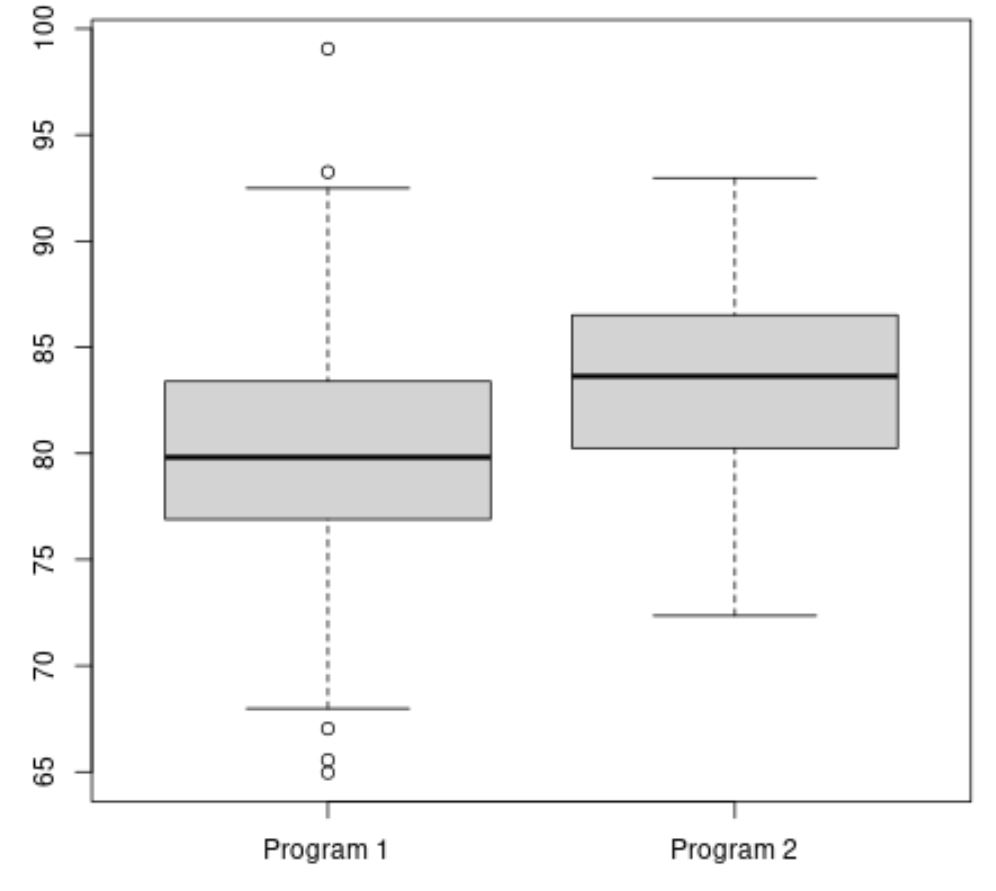
Nilai ujian rata-rata untuk Program 2 tampaknya lebih tinggi, namun perbedaan nilai ujian antara kedua program tersebut kira-kira sama.

Kode berikut menunjukkan cara melakukan uji-t sampel independen dengan uji-t Welch:

 #perform independent samples t-test
t. test (program1, program2, var. equal = TRUE )

	Two Sample t-test

data: program1 and program2
t = -3.3348, df = 518, p-value = 0.0009148
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -6.111504 -1.580245
sample estimates:
mean of x mean of y 
 80.11322 83.95910

#perform Welch's two sample t-test
t. test (program1, program2, var. equal = FALSE )

	Welch Two Sample t-test

data: program1 and program2
t = -3.3735, df = 20.589, p-value = 0.00293
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -6.219551 -1.472199
sample estimates:
mean of x mean of y 
 80.11322 83.95910 

Uji-t sampel independen menghasilkan nilai p sebesar 0,0009 dan uji-t Welch menghasilkan nilai p sebesar 0,0029 .

Karena nilai p setiap tes kurang dari 0,05, kami akan menolak hipotesis nol di setiap tes dan menyimpulkan bahwa terdapat perbedaan yang signifikan secara statistik dalam nilai rata-rata ujian antara kedua program.

Meskipun ukuran sampelnya tidak sama, uji t sampel independen dan uji t Welch memberikan hasil yang serupa karena kedua sampel memiliki varian yang sama.

Contoh 2: Ukuran sampel yang tidak sama dan varians yang tidak sama

Misalkan kita mengelola dua program yang dirancang untuk membantu siswa berprestasi lebih baik pada ujian tertentu.

Hasilnya adalah sebagai berikut:

Program 1:

• n (ukuran sampel): 500
• x (rata-rata sampel): 80
• s (deviasi standar sampel): 25

Program 2:

• n (ukuran sampel): 20
• x (rata-rata sampel): 85
• s (deviasi standar sampel): 5

Kode berikut menunjukkan cara membuat boxplot di R untuk memvisualisasikan distribusi nilai ujian untuk setiap program:

 #make this example reproducible
set. seeds (1)

#create vectors to hold exam scores
program1 <- rnorm(500, mean=80, sd=25)
program2 <- rnorm(20, mean=85, sd=5)

#create boxplots to visualize distribution of exam scores
boxplot(program1, program2, names=c(" Program 1 "," Program 2 "))

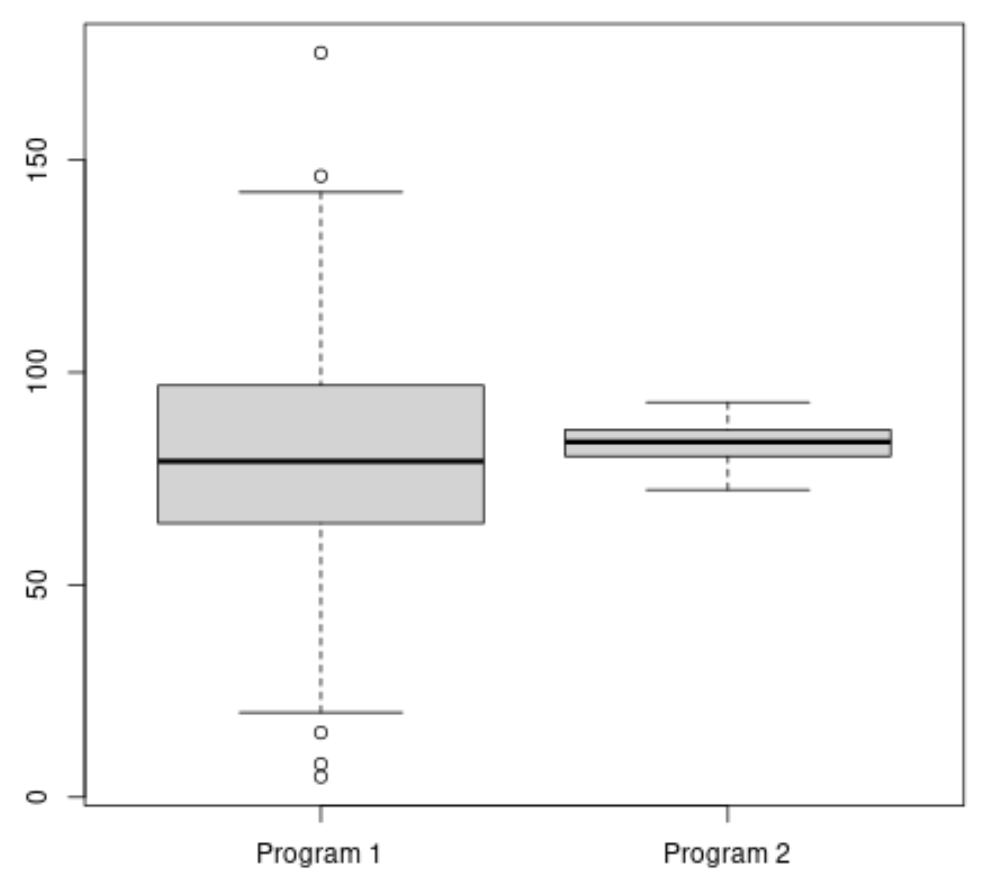
Nilai ujian rata-rata untuk Program 2 tampaknya lebih tinggi, namun varians nilai ujian untuk Program 1 jauh lebih tinggi dibandingkan dengan Program 2.

Kode berikut menunjukkan cara melakukan uji-t sampel independen dengan uji-t Welch:

 #perform independent samples t-test
t. test (program1, program2, var. equal = TRUE )

	Two Sample t-test

data: program1 and program2
t = -0.5988, df = 518, p-value = 0.5496
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -14.52474 7.73875
sample estimates:
mean of x mean of y 
  80.5661 83.9591

#perform Welch's two sample t-test
t. test (program1, program2, var. equal = FALSE )

	Welch Two Sample t-test

data: program1 and program2
t = -2.1338, df = 74.934, p-value = 0.03613
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -6.560690 -0.225296
sample estimates:
mean of x mean of y 
  80.5661 83.9591 

Uji-t sampel independen menghasilkan nilai p sebesar 0,5496 dan uji-t Welch menghasilkan nilai p sebesar 0,0361 .

Uji t sampel independen tidak mampu mendeteksi perbedaan rata-rata nilai ujian, namun uji t Welch mampu mendeteksi perbedaan signifikan secara statistik.

Karena kedua sampel memiliki varians yang tidak sama, hanya uji-t Welch yang mampu mendeteksi perbedaan rata-rata nilai ujian yang signifikan secara statistik, karena tes ini tidak mengasumsikan varians yang sama antar sampel .

Sumber daya tambahan

Tutorial berikut memberikan informasi tambahan tentang uji-t:

Pengantar uji-t satu sampel
Pengantar uji t dua sampel
Pengantar uji-t sampel berpasangan