Excel: cara menggunakan linest untuk melakukan regresi linier berganda
Anda bisa menggunakan fungsi LINEST di Excel untuk menyesuaikan model regresi linier berganda dengan sekumpulan data.
Fungsi ini menggunakan sintaks dasar berikut:
= LINEST ( known_y's, [known_x's], [const], [stats] )
Emas:
- unknown_y’s : array nilai y yang diketahui
- unknown_x’s : array nilai x yang diketahui
- const : Argumen opsional. Jika TRUE, konstanta b diproses secara normal. Jika FALSE, konstanta b diatur ke 1.
- statistik : Argumen opsional. Jika BENAR, statistik regresi tambahan akan dikembalikan. Jika FALSE, statistik regresi tambahan tidak dikembalikan.
Contoh langkah demi langkah berikut menunjukkan cara menggunakan fungsi ini dalam praktiknya.
Langkah 1: Masukkan datanya
Pertama, mari masukkan kumpulan data berikut ke dalam Excel:
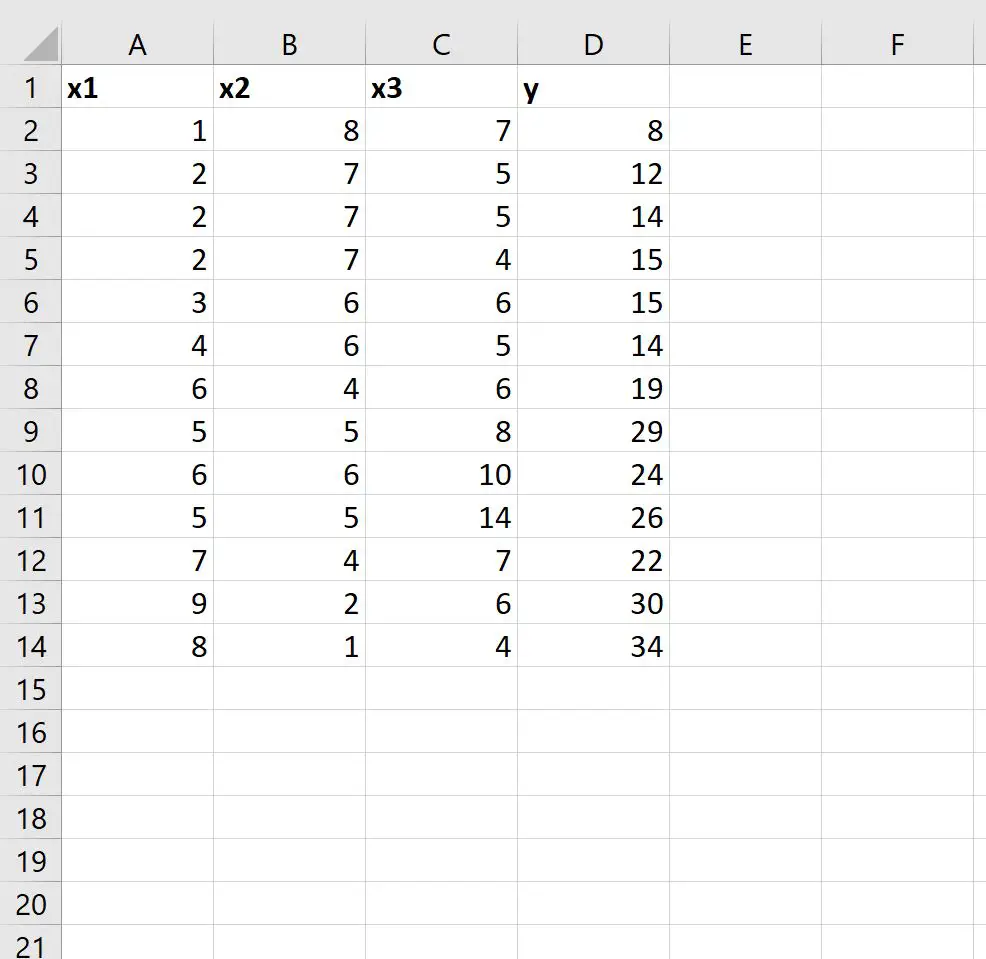
Langkah 2: Gunakan LINEST agar sesuai dengan model regresi linier berganda
Misalkan kita ingin menyesuaikan model regresi linier berganda dengan menggunakan x1 , x2 , dan x3 sebagai variabel prediktor dan y sebagai variabel respon.
Untuk melakukan ini, kita dapat mengetikkan rumus berikut di sel mana pun agar sesuai dengan model regresi linier berganda ini
=LINEST( D2:D14 , A2:C14 )
Tangkapan layar berikut menunjukkan cara menggunakan rumus ini dalam praktik:
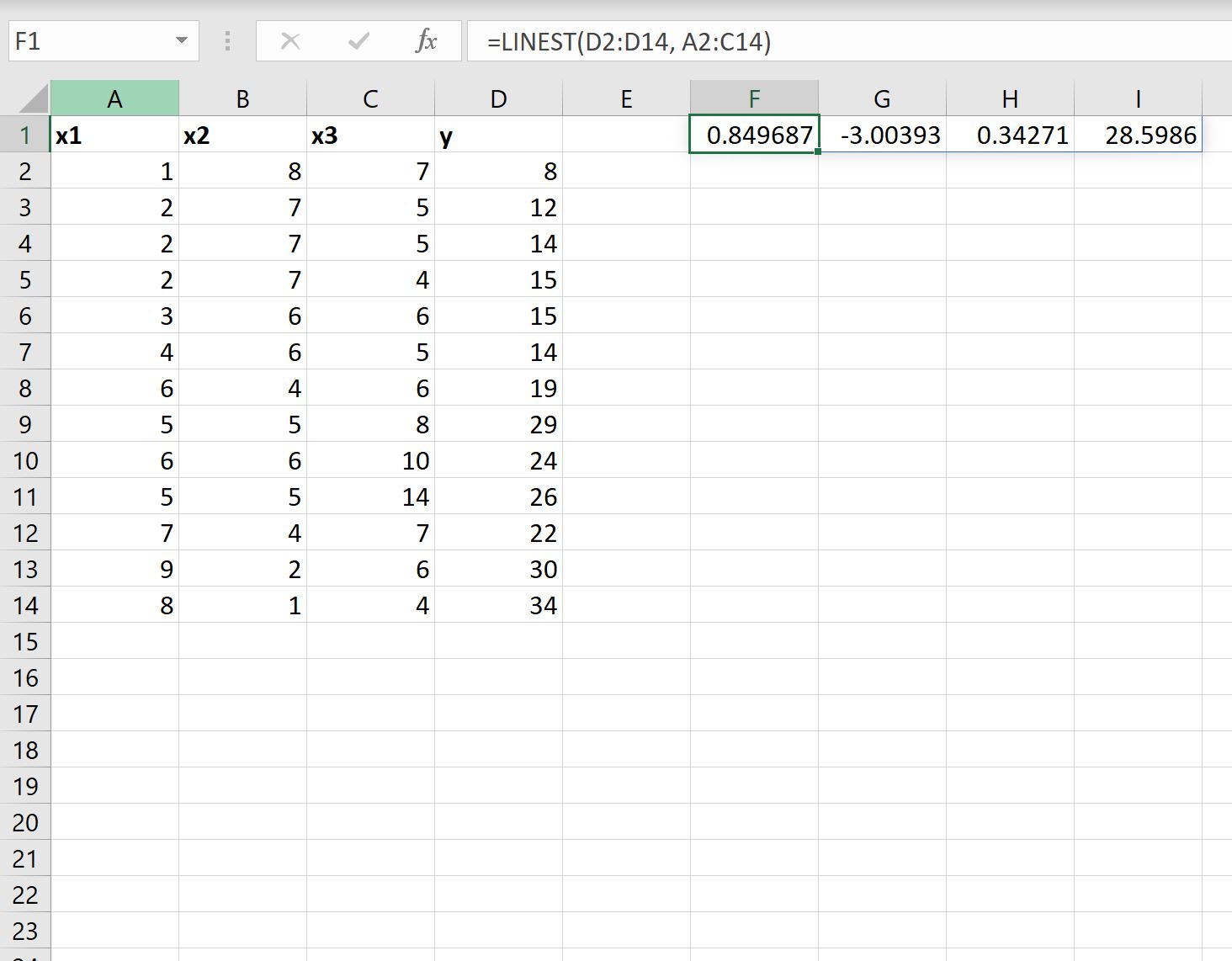
Berikut cara menafsirkan hasilnya:
- Koefisien intersepnya adalah 28,5986 .
- Koefisien untuk x1 adalah 0,34271 .
- Koefisien untuk x2 adalah -3,00393 .
- Koefisien untuk x3 adalah 0,849687 .
Dengan menggunakan koefisien-koefisien ini, kita dapat menulis persamaan regresi yang sesuai sebagai berikut:
kamu = 28,5986 + 0,34271(x1) – 3,00393(x2) + 0,849687(x3)
Langkah 3 (Opsional): Lihat statistik regresi tambahan
Kita juga dapat mengatur nilai argumen stats dalam fungsi LINEST sama dengan TRUE untuk menampilkan statistik regresi tambahan untuk persamaan regresi yang sesuai:
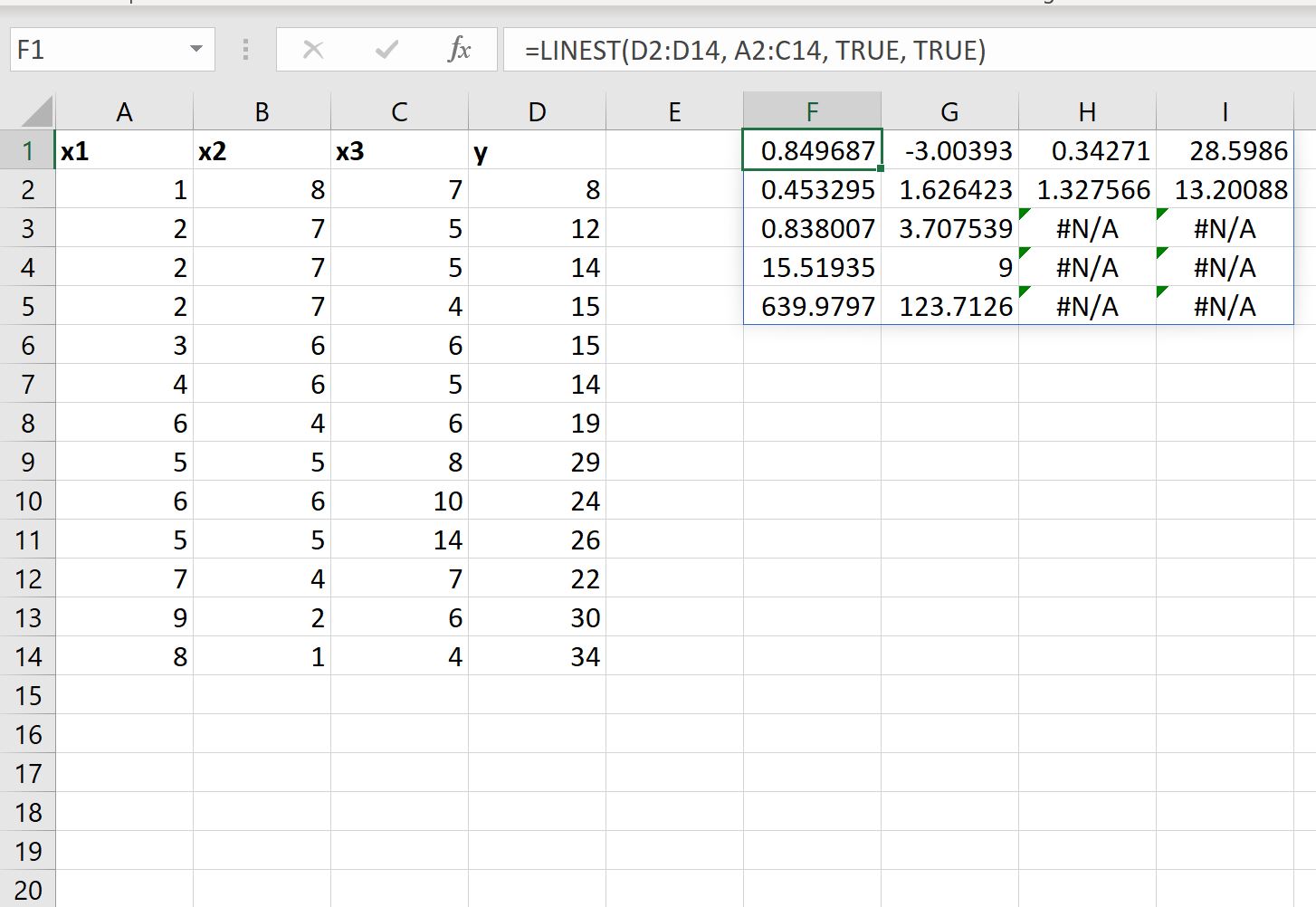
Persamaan regresi yang dipasang masih sama:
kamu = 28,5986 + 0,34271(x1) – 3,00393(x2) + 0,849687(x3)
Berikut cara menginterpretasikan nilai lain dari hasil:
- Kesalahan standar untuk x3 adalah 0.453295 .
- Kesalahan standar untuk x2 adalah 1.626423 .
- Kesalahan standar untuk x1 adalah 1.327566 .
- Kesalahan standar untuk intersepsi adalah 13.20088 .
- R 2 modelnya adalah .838007 .
- Kesalahan standar sisa untuk y adalah 3.707539 .
- Statistik F keseluruhan adalah 15.51925 .
- Derajat kebebasannya adalah 9 .
- Jumlah regresi kuadrat adalah 639.9797 .
- Jumlah sisa kuadrat adalah 123.7126 .
Secara umum, ukuran yang paling menarik dalam statistik tambahan ini adalah nilai R 2 , yang mewakili proporsi varians variabel respon yang dapat dijelaskan oleh variabel prediktor.
Nilai R 2 dapat bervariasi dari 0 hingga 1.
Karena R 2 model khusus ini adalah 0,838 , hal ini menunjukkan bahwa variabel prediktor berfungsi dengan baik dalam memprediksi nilai variabel respons y.
Terkait: Berapa nilai R-kuadrat yang bagus?
Sumber daya tambahan
Tutorial berikut menjelaskan cara melakukan operasi umum lainnya di Excel:
Cara menggunakan fungsi LOGEST di Excel
Cara melakukan regresi nonlinier di Excel
Cara melakukan regresi kubik di Excel