Cara melakukan regresi ols dengan python (dengan contoh)

Regresi kuadrat terkecil biasa (OLS) adalah metode yang memungkinkan kita menemukan garis yang paling menggambarkan hubungan antara satu atau lebih variabel prediktor dan variabel respons .

Metode ini memungkinkan kita menemukan persamaan berikut:

ŷ = b ₀ + b ₁ x

Emas:

• ŷ : Perkiraan nilai respons
• b ₀ : Asal garis regresi
• b ₁ : Kemiringan garis regresi

Persamaan ini dapat membantu kita memahami hubungan antara prediktor dan variabel respon, dan dapat digunakan untuk memprediksi nilai variabel respon dengan mempertimbangkan nilai variabel prediktor.

Contoh langkah demi langkah berikut menunjukkan cara melakukan regresi OLS dengan Python.

Langkah 1: Buat datanya

Untuk contoh ini, kita akan membuat dataset yang berisi dua variabel berikut untuk 15 siswa:

• Jumlah total jam belajar
• Hasil ujian

Kami akan melakukan regresi OLS, menggunakan jam sebagai variabel prediktor dan nilai ujian sebagai variabel respon.

Kode berikut menunjukkan cara membuat dataset palsu ini di pandas:

 import pandas as pd

#createDataFrame
df = pd. DataFrame ({' hours ': [1, 2, 4, 5, 5, 6, 6, 7, 8, 10, 11, 11, 12, 12, 14],
                   ' score ': [64, 66, 76, 73, 74, 81, 83, 82, 80, 88, 84, 82, 91, 93, 89]})

#view DataFrame
print (df)

    hours score
0 1 64
1 2 66
2 4 76
3 5 73
4 5 74
5 6 81
6 6 83
7 7 82
8 8 80
9 10 88
10 11 84
11 11 82
12 12 91
13 12 93
14 14 89

Langkah 2: Lakukan regresi OLS

Selanjutnya, kita dapat menggunakan fungsi dalam modul statsmodels untuk melakukan regresi OLS, menggunakan jam sebagai variabel prediktor dan skor sebagai variabel respons :

 import statsmodels.api as sm

#define predictor and response variables
y = df[' score ']
x = df[' hours ']

#add constant to predictor variables
x = sm. add_constant (x)

#fit linear regression model
model = sm. OLS (y,x). fit ()

#view model summary
print ( model.summary ())

                            OLS Regression Results                            
==================================================== ============================
Dept. Variable: R-squared score: 0.831
Model: OLS Adj. R-squared: 0.818
Method: Least Squares F-statistic: 63.91
Date: Fri, 26 Aug 2022 Prob (F-statistic): 2.25e-06
Time: 10:42:24 Log-Likelihood: -39,594
No. Observations: 15 AIC: 83.19
Df Residuals: 13 BIC: 84.60
Model: 1                                         
Covariance Type: non-robust                                         
==================================================== ============================
                 coef std err t P>|t| [0.025 0.975]
-------------------------------------------------- ----------------------------
const 65.3340 2.106 31.023 0.000 60.784 69.884
hours 1.9824 0.248 7.995 0.000 1.447 2.518
==================================================== ============================
Omnibus: 4,351 Durbin-Watson: 1,677
Prob(Omnibus): 0.114 Jarque-Bera (JB): 1.329
Skew: 0.092 Prob(JB): 0.515
Kurtosis: 1.554 Cond. No. 19.2
==================================================== ============================

Dari kolom koefisien , kita dapat melihat koefisien regresi dan menulis persamaan regresi berikut:

Skor = 65.334 + 1.9824*(jam)

Artinya, setiap tambahan jam belajar dikaitkan dengan peningkatan rata-rata nilai ujian sebesar 1,9824 poin.

Nilai awal sebesar 65.334 memberi tahu kita rata-rata nilai ujian yang diharapkan untuk seorang siswa yang belajar selama nol jam.

Kita juga dapat menggunakan persamaan ini untuk mencari nilai ujian yang diharapkan berdasarkan jumlah jam belajar seorang siswa.

Misalnya, seorang siswa yang belajar selama 10 jam harus mencapai nilai ujian 85.158 :

Skor = 65.334 + 1.9824*(10) = 85.158

Berikut cara menafsirkan ringkasan model lainnya:

• P(>|t|): Ini adalah nilai p yang terkait dengan koefisien model. Karena nilai p untuk jam (0,000) kurang dari 0,05, kita dapat mengatakan bahwa terdapat hubungan yang signifikan secara statistik antara jam dan skor .
• R-squared: Hal ini menunjukkan bahwa persentase variasi nilai ujian dapat dijelaskan oleh jumlah jam belajar. Dalam hal ini, 83,1% variasi skor dapat dijelaskan oleh jam belajar.
• F-statistik dan nilai p: F-statistik ( 63,91 ) dan nilai p yang sesuai ( 2,25e-06 ) memberi tahu kita signifikansi model regresi secara keseluruhan, yaitu apakah variabel prediktor dalam model berguna dalam menjelaskan variasi. dalam variabel respon. Karena nilai p dalam contoh ini kurang dari 0,05, model kami signifikan secara statistik dan jam dianggap berguna dalam menjelaskan variasi skor .

Langkah 3: Visualisasikan garis yang paling sesuai

Terakhir, kita dapat menggunakan paket visualisasi data matplotlib untuk memvisualisasikan garis regresi yang disesuaikan dengan titik data sebenarnya:

 import matplotlib. pyplot as plt

#find line of best fit
a, b = np. polyfit (df[' hours '], df[' score '], 1 )

#add points to plot
plt. scatter (df[' hours '], df[' score '], color=' purple ')

#add line of best fit to plot
plt. plot (df[' hours '], a*df[' hours ']+b)

#add fitted regression equation to plot
plt. text ( 1 , 90 , 'y = ' + '{:.3f}'.format(b) + ' + {:.3f}'.format(a) + 'x', size= 12 )

#add axis labels
plt. xlabel (' Hours Studied ')
plt. ylabel (' Exam Score ')

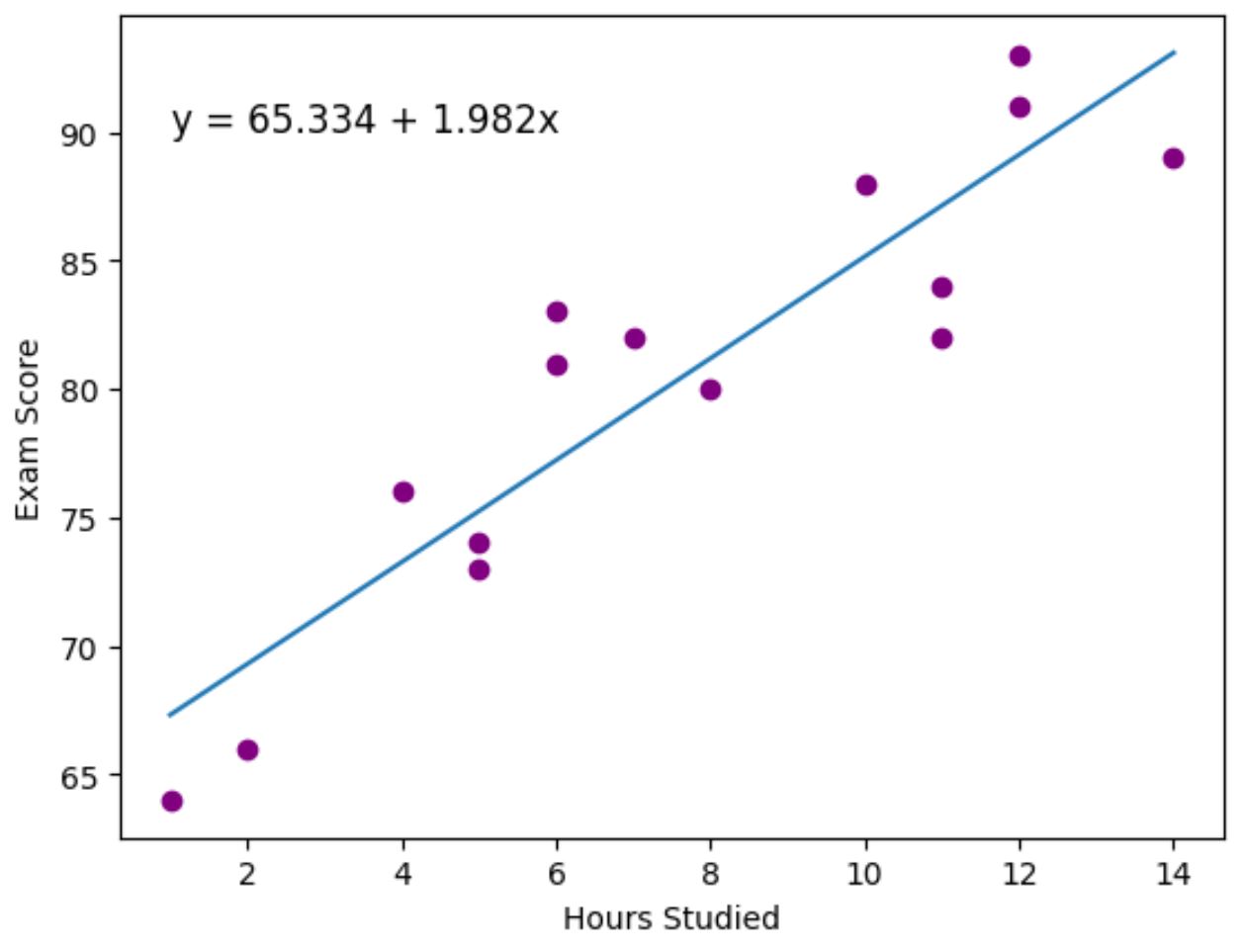
Titik ungu mewakili titik data aktual dan garis biru mewakili garis regresi yang sesuai.

Kami juga menggunakan fungsi plt.text() untuk menambahkan persamaan regresi yang sesuai ke sudut kiri atas plot.

Melihat grafik tersebut, terlihat bahwa garis regresi yang dipasang menunjukkan hubungan antara variabel jam kerja dan variabel skor dengan cukup baik.

Sumber daya tambahan

Tutorial berikut menjelaskan cara melakukan tugas umum lainnya dengan Python:

Cara Melakukan Regresi Logistik dengan Python
Cara Melakukan Regresi Eksponensial dengan Python
Cara menghitung AIC model regresi dengan Python