Cara membaca plot kotak dengan pencilan (dengan contoh)

Plot kotak adalah jenis plot yang menampilkan ringkasan lima digit kumpulan data, yang meliputi:

• Nilai minimum
• Kuartil pertama (persentil ke-25)
• Nilai median
• Kuartil ketiga (persentil ke-75)
• Nilai maksimum

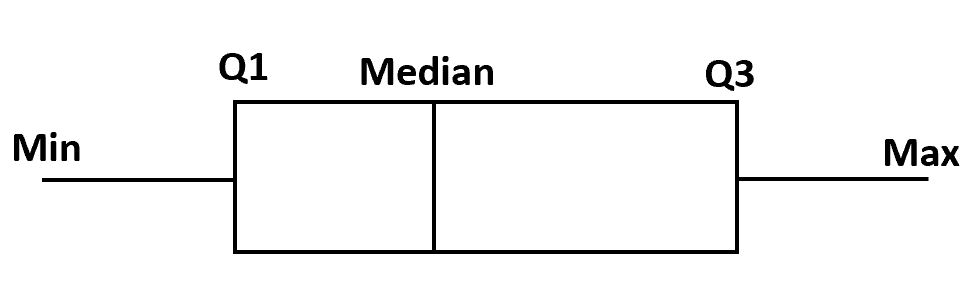
Untuk membuat plot kotak, pertama-tama kita menggambar kotak dari kuartil pertama hingga kuartil ketiga.

Selanjutnya, kita menggambar garis vertikal di median.

Terakhir, kita menarik “kumis” kuartil hingga nilai minimum dan maksimum.

Di sebagian besar perangkat lunak statistik, suatu observasi didefinisikan sebagai outlier jika memenuhi salah satu dari dua persyaratan berikut:

• Pengamatannya 1,5 kali rentang antarkuartil di bawah kuartil pertama (Q1)
• Pengamatannya 1,5 kali rentang antarkuartil di atas kuartil ketiga (Q3).

Jika ada outlier dalam kumpulan data, biasanya diberi label dengan titik kecil di luar rentang kumis di plot kotak:

Jika hal ini terjadi, nilai “minimum” dan “maksimum” dalam diagram kotak hanya diberi nilai masing-masing Q1 – 1,5*IQR dan Q3 + 1,5*IQR.

Contoh berikut menunjukkan cara menafsirkan plot kotak dengan dan tanpa outlier.

Contoh: Menafsirkan Plot Kotak dengan Pencilan

Misalkan kita membuat dua plot kotak berikut untuk memvisualisasikan distribusi poin yang dicetak oleh pemain bola basket dari dua tim berbeda:

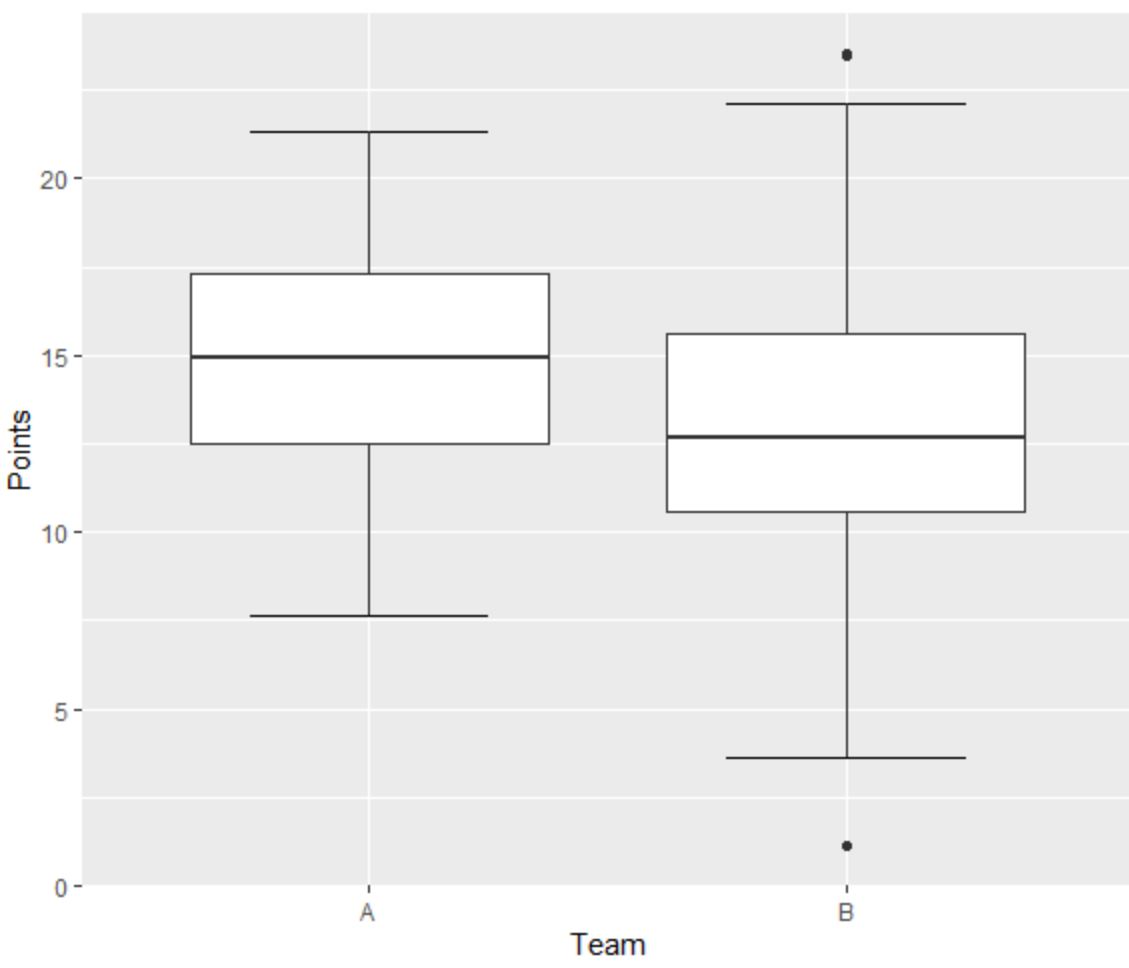
Plot kotak kiri untuk Tim A tidak memiliki outlier karena tidak ada titik kecil yang terletak di luar batas minimum dan maksimum.

Namun, diagram kotak yang tepat untuk Tim B memiliki satu outlier di atas nilai “maksimum” dan satu outlier di bawah nilai “minimum”.

Berikut adalah ringkasan lima digit terkini untuk distribusi variabel “Poin” untuk Tim B:

• Nilai minimal: 1.1
• Kuartil pertama: 10.5
• Median: 12.7
• Kuartil ketiga: 15.6
• Nilai maksimum: 23,5

Berikut cara menghitung batas potensi outlier:

Skala antarkuartil : Kuartil ketiga – Kuartil pertama = 15,6 – 10,5 = 5,1

Batas bawah : Q1 – 1.5*IQR = 10.5 – 1.5*5.1 = 2.85

Batas atas : Q3 + 1.5*IQR = 15.6 + 1.5*5.1 = 23.25

Whisker untuk nilai minimum dan maksimum pada boxplot ditempatkan pada 2.85 dan 23.25 .

Dengan demikian, observasi dengan nilai 1,1 dan 23,5 sama-sama memenuhi syarat sebagai outlier dalam boxplot karena berada di luar batas bawah dan batas atas.

Bonus : Berikut adalah kode persis yang kami gunakan untuk membuat dua plot kotak ini dalam bahasa pemrograman R:

 library (ggplot2)

#make this example reproducible 
set. seeds (2)

#create data frame
df <- data. frame (Team = factor(rep(c("A", "B"), each = 200)), 
                 Points = c(rnorm(200, mean = 15, sd = 3), 
                           rnorm(200, mean = 12, sd = 4))) 

#create box plots
ggplot(df, aes(x = Team, y = Points)) +
  stat_boxplot(geom = " errorbar ", width = 0.5) +  
  geom_boxplot() 

#calculate summary statistics for each team
tapply(df$Points, df$Team, summary)

Sumber daya tambahan

Tutorial berikut memberikan informasi tambahan tentang plot kotak:

Bagaimana Membandingkan Plot Kotak
Cara Mengidentifikasi Asimetri pada Plot Kotak
Cara mencari rentang interkuartil pada diagram kotak