Cara menghitung skor z di sas
Dalam statistik, skor-z memberi tahu kita berapa banyak standar deviasi suatu nilai dari mean .
Kami menggunakan rumus berikut untuk menghitung skor-z:
z = (X – μ) / σ
Emas:
- X adalah nilai data mentah tunggal
- μ adalah rata-rata kumpulan data
- σ adalah deviasi standar kumpulan data
Contoh berikut menunjukkan cara menghitung skor-z untuk nilai data mentah di SAS.
Contoh: Hitung Z-score di SAS
Misalkan kita membuat dataset berikut di SAS:
/*create dataset*/ data original_data; input values; datalines ; 7 12 14 12 16 18 6 7 14 17 19 22 24 13 17 12 ; run ; /*view dataset*/ proc print data = original_data;
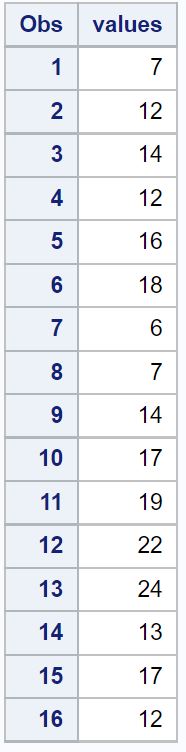
Sekarang misalkan kita ingin menghitung skor-z untuk setiap nilai dalam kumpulan data.
Kita dapat menggunakan proc sql untuk melakukan ini:
/*create new variable that shows z-scores for each raw data value*/
proc sql ;
select values, (values - mean(values)) / std(values) as z_scores
from original_data;
quit ;
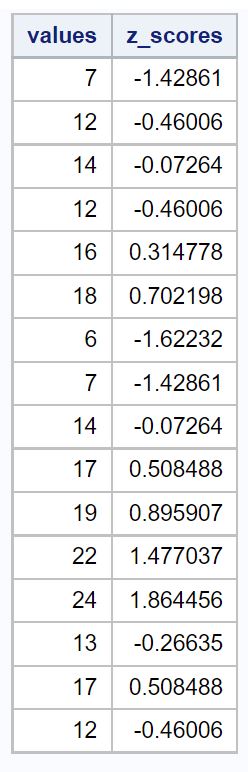
Kolom nilai menampilkan nilai data asli dan kolom z_scores menampilkan skor z untuk setiap nilai.
Bagaimana menafsirkan skor Z di SAS
Skor-z memberi tahu kita berapa banyak deviasi standar suatu nilai dari mean.
Skor z bisa positif, negatif, atau nol.
Skor z yang positif menunjukkan bahwa suatu nilai tertentu berada di atas rata-rata, skor z yang negatif menunjukkan bahwa suatu nilai tertentu berada di bawah rata-rata, dan skor az yang bernilai nol menunjukkan bahwa suatu nilai tertentu sama dengan rata-rata.
Jika kita menghitung mean dan deviasi standar kumpulan data kita, kita akan menemukan bahwa meannya adalah 14,375 dan standar deviasinya adalah 5,162 .
Jadi nilai pertama di dataset kita adalah 7, yang memiliki z-score (7-14.375) / 5.162 = -1.428 . Artinya nilai “7” lebih rendah standar deviasinya sebesar 1,428 dari mean.
Nilai berikutnya dalam data kami, 12, memiliki skor-z (12-14.375) / 5.162 = -0.46 . Artinya nilai “12” adalah 0,46 standar deviasi lebih rendah dari mean.
Semakin jauh suatu nilai dari mean, semakin tinggi nilai absolut skor-z untuk nilai tersebut.
Misalnya, nilai 7 lebih jauh dari mean (14,375) dibandingkan nilai 12, yang menjelaskan mengapa 7 memiliki skor-z dengan nilai absolut lebih besar.
Sumber daya tambahan
Artikel berikut menjelaskan cara melakukan tugas umum lainnya di SAS:
Cara mengidentifikasi outlier di SAS
Cara menghitung persentil di SAS
Cara menghitung mean, median dan modus di SAS