Kartu kendali u

Oleh Benjamin anderson Agustus 1, 2023 Manajemen mutu 0 Komentar

Pada artikel kali ini kami akan menjelaskan kepada Anda apa itu kartu kendali U, apa saja ciri-cirinya dan kegunaannya. Selain itu, Anda akan dapat melihat bagaimana bagan kendali U dibuat dan latihan diselesaikan langkah demi langkah.

Apa itu kartu kendali U?

Bagan kendali U , atau sederhananya bagan U , adalah bagan yang mewakili berapa kali suatu fenomena terjadi per unit pengukuran jika fenomena tersebut bersifat variabel.

Misalnya, peta kendali U dapat digunakan untuk mengontrol jumlah cacat per meter persegi kain. Seringkali sampel kain tidak dapat diambil dengan luas permukaan yang sama, sehingga setiap sampel berbeda. Dengan demikian, bagan U memungkinkan kita mempelajari proses yang memiliki ukuran sampel yang bervariasi.

Penting untuk dicatat bahwa peta kendali U tidak mewakili jumlah unit yang cacat, namun jumlah cacat yang dimiliki setiap unit, seperti pada grafik C. Sebaliknya, peta kendali P atau NP mengontrol proporsi dan jumlah produk cacat. Di bawah ini kita akan melihat perbedaan antara semua jenis diagram kendali.

Perlu diingat bahwa model matematika referensi dari peta kendali U adalah distribusi Poisson, karena kita mempelajari jumlah kemunculan suatu fenomena per unit pengukuran.

➤ Lihat: Distribusi Ikan

Cara Membuat Bagan Kendali U

Sekarang setelah kita mengetahui definisi dari diagram kendali U, mari kita lihat bagaimana diagram kendali jenis ini dibuat:

Pengambilan sampel : pertama, sampel yang berbeda harus diambil untuk melihat evolusi fenomena yang akan diukur. Sampel harus berukuran sama, selain itu disarankan mengambil minimal 20 sampel.
Tentukan berapa kali fenomena tersebut terjadi per unit pengukuran : untuk setiap sampel, berapa kali fenomena yang akan dipelajari diulang.
Hitung nilai rata-rata kejadian : dari data yang dikumpulkan perlu dihitung rata-rata frekuensi terjadinya fenomena per satuan pengukuran.

$\overline{u}=\cfrac{\text{N\'umero de veces que ocurre el fen\'omeno}}{\text{N\'umero total de unidades de todas las muestras}}$

Hitung Batas Kontrol U-Card – Batas kontrol U-Card kemudian harus dihitung menggunakan rumus yang diberikan di bawah ini. Perlu diingat bahwa nilai batas kendali bervariasi tergantung pada ukuran sampel.

$\displaystyle LCS_i=\overline{u}+3\sqrt{\frac{\overline{u}}{n_i}$

$\displaystyle LCI_i=\overline{u}-3\sqrt{\frac{\overline{u}}{n_i}$

Emas

$LCS_i$

Dan

$LCI_i$

masing-masing adalah batas kendali atas dan bawah sampel i,

$\overline{u}$

adalah nilai rata-rata kejadian dan

$n_i$

adalah ukuran sampel i.

Merencanakan nilai pada peta – Nilai yang dikumpulkan beserta batas kendali yang dihitung sekarang harus diplot pada peta untuk membuat diagram kendali U.
Analisis kartu kendali U : pada akhirnya yang tersisa hanyalah memeriksa bahwa tidak ada nilai pada kartu yang berada di luar batas kendali dan oleh karena itu prosesnya terkendali. Jika tidak, tindakan harus diambil untuk memperbaiki proses tersebut.

Contoh kartu kendali U

Sebuah perusahaan industri ingin mengendalikan jumlah cacat per ^m2 kain. Tabel berikut menyajikan sampel yang dianalisis dan jumlah cacat yang ditemukan. Buatlah diagram kendali U untuk mempelajari jumlah cacat.

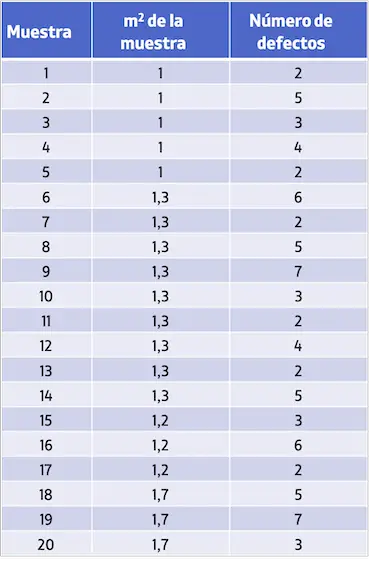
Untuk membuat peta kendali U, Anda harus menghitung terlebih dahulu nilai rata-rata jumlah cacat per sampel:

$\overline{u}=\cfrac{\text{N\'umero de veces que ocurre el fen\'omeno}}{\text{N\'umero total de unidades}}=\cfrac{78}{25,4}=3,07$

Sekarang kita perlu menghitung batas kendali untuk setiap sampel. Sebagai contoh, batas kendali untuk sampel pertama dihitung di bawah ini:

$\displaystyle LCS_1=\overline{u}+3\sqrt{\frac{\overline{u}}{n_1}}=3,07+3\sqrt{\frac{3,07}{1}}=8,33$

$\displaystyle LCI_1=\overline{u}-3\sqrt{\frac{\overline{u}}{n_1}}=3,07-3\sqrt{\frac{3,07}{1}}=-2,19$

Semua batas kendali bawah menghasilkan angka negatif, yang tidak masuk akal. Oleh karena itu, kami akan menetapkan batas kendali bawah ke 0.

Dengan demikian, nilai batas kendali setiap sampel adalah sebagai berikut:

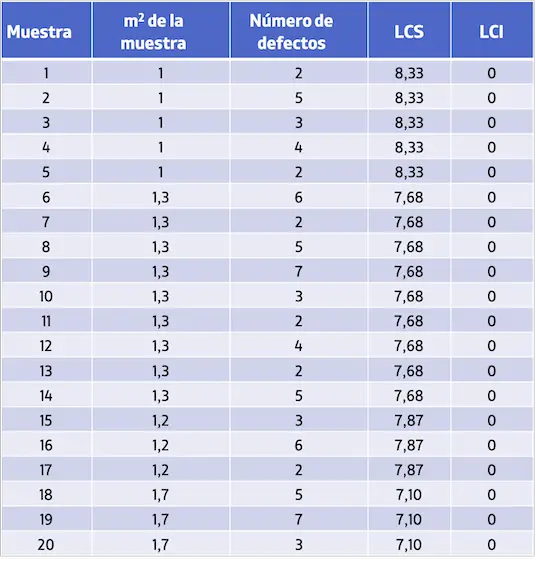
Terakhir, cukup merepresentasikan semua nilai dalam suatu grafik untuk mendapatkan peta kendali U:

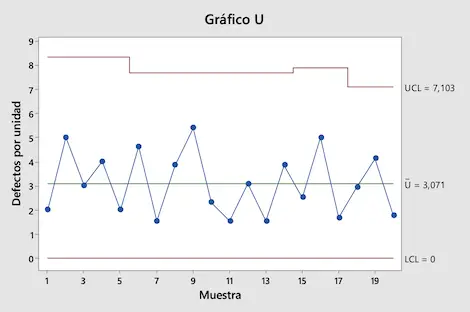
Seperti yang terlihat pada grafik U yang kita buat, semua nilai berada di antara batas kendali. Oleh karena itu, kami dapat menyimpulkan bahwa proses produksi terkendali.

Jenis Bagan Kontrol Lainnya

Selain bagan U, ada jenis bagan kendali atribut lainnya:

Kartu kendali P : proporsi produk cacat dikendalikan.
Kartu kendali NP : jumlah produk cacat dikontrol.
Peta kendali C : Jumlah cacat dikontrol seperti pada grafik U, tetapi ukuran sampelnya konstan.

Tentang Penulis

Benjamin anderson

Halo, saya Benjamin, pensiunan profesor statistika yang menjadi guru Statorial yang berdedikasi. Dengan pengalaman dan keahlian yang luas di bidang statistika, saya ingin berbagi ilmu untuk memberdayakan mahasiswa melalui Statorials. Baca selengkapnya