Teorema limit pusat

Artikel ini menjelaskan apa itu teorema limit pusat (CLT) dan kegunaannya dalam statistik. Anda juga akan menemukan rumus teorema limit pusat dan contoh penerapannya yang diselesaikan langkah demi langkah.

Apa teorema limit pusat?

Dalam statistik, teorema batas pusat , juga disebut teorema batas pusat , menyatakan bahwa distribusi rata-rata sampel mendekati distribusi normal seiring bertambahnya ukuran sampel, terlepas dari distribusi probabilitas populasi.

Artinya, teorema limit pusat menyatakan bahwa jika kita mengambil sampel dalam jumlah yang cukup besar, rata-rata sampel tersebut dapat diperkirakan berdistribusi normal.

Selain itu, teorema limit pusat menyatakan bahwa mean sampel akan mendekati nilai mean populasi seiring dengan bertambahnya ukuran sampel. Hal ini memungkinkan kami memperkirakan parameter populasi statistik. Di bawah ini kita akan melihat bagaimana hal ini dilakukan.

Secara umum, untuk menerapkan teorema limit pusat, jumlah sampel harus minimal 30 observasi, meskipun hal ini tergantung pada karakteristik variabel yang diteliti.

Teorema limit pusat memiliki banyak penerapan, karena distribusi normal memungkinkan penghitungan statistik inferensial, seperti pengujian hipotesis atau interval kepercayaan. Misalnya, di bidang keuangan, teorema batas pusat digunakan untuk menganalisis pengembalian dan risiko suatu investasi.

Contoh teorema limit pusat

Setelah kita melihat definisi teorema limit pusat, mari kita lihat contohnya untuk memahami maknanya sepenuhnya.

Contoh teorema limit pusat adalah pelemparan sebuah dadu. Pelemparan dadu mengikuti distribusi seragam yang diskrit , karena semua hasil mempunyai peluang yang sama. Namun distribusi jumlah beberapa hasil mendekati distribusi normal.

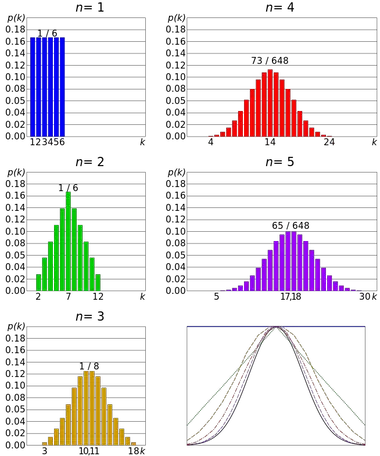
Dengan demikian, semakin banyak lemparan maka semakin besar kemungkinan bentuk distribusi mean cenderung menyerupai grafik distribusi normal.

Rumus Teorema Limit Pusat

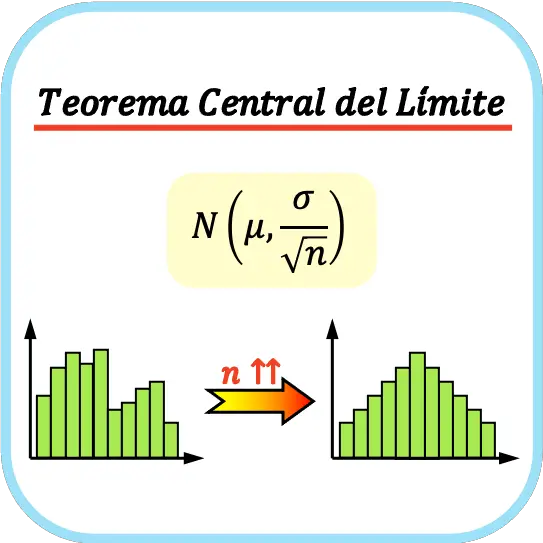
Teorema limit pusat menyatakan bahwa jika suatu populasi mempunyai mean μ dan simpangan baku σ dan kita mengambil jumlah sampel yang cukup besar (n≥30), himpunan mean sampel dapat didekati dengan distribusi normal dengan mean μ dan simpangan baku σ /√n.

Selanjutnya _jika X _{1 ,} maka berdistribusi normal ditentukan dengan rumus berikut:

Latihan terpecahkan dari teorema limit pusat

Agar Anda dapat sepenuhnya mengasimilasi konsep tersebut, berikut adalah latihan teorema limit pusat yang telah diselesaikan.

• Sebuah perusahaan menjual suku cadang yang digunakan untuk menggantikan komponen mainan tertentu. Sebuah koin mempunyai berat rata-rata 300 gram dan simpangan baku 50 gram. Jika seorang pelanggan memesan 100 buah dalam jumlah banyak, berapa peluang berat rata-rata potongan dalam satu batch lebih besar dari 305 g? Dan berapa peluang terambilnya 100 buah beratnya lebih dari 31 kg?

Karena ukuran batchnya besar (n=100), kita dapat menerapkan teorema limit pusat untuk menyelesaikan masalah tersebut.

Jadi, dengan menggunakan rumus teorema limit pusat, distribusi mean sampel dapat diperkirakan berdistribusi normal dengan parameter berikut:

Sekarang kita melakukan proses pengetikan sehingga kita dapat menemukan probabilitas yang diminta oleh latihan tersebut. Untuk melakukan ini, kita perlu mengurangi mean dari distribusi lalu membaginya dengan deviasi standar:

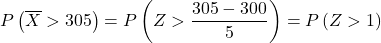tabel distribusi normal :

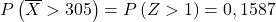
Jadi kita ulangi proses pengetikan, lalu cari probabilitas kedua yang ditanyakan soal kepada kita:

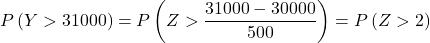
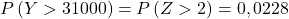➤ Lihat: Hukum bilangan besar