Probabilitas bersyarat (atau probabilitas bersyarat)

Oleh Benjamin anderson Agustus 6, 2023 Kemungkinan 0 Komentar

Di sini Anda akan mengetahui apa itu probabilitas bersyarat (atau probabilitas bersyarat). Kami menjelaskan bagaimana probabilitas bersyarat dihitung dengan contoh dan properti dari jenis probabilitas ini. Selain itu, Anda akan dapat berlatih dengan latihan probabilitas bersyarat yang diselesaikan selangkah demi selangkah.

Apa yang dimaksud dengan probabilitas bersyarat?

Probabilitas bersyarat , disebut juga probabilitas bersyarat , adalah ukuran statistik yang menunjukkan probabilitas terjadinya peristiwa A jika peristiwa B lain terjadi. Artinya, probabilitas bersyarat P(A|B) mengacu pada probabilitas kejadian A terjadi setelah kejadian B terjadi.

Probabilitas bersyarat ditulis dengan garis vertikal di antara dua kejadian: P(A|B), dan berbunyi: “probabilitas bersyarat dari kejadian A kejadian tertentu B”.

Perhatikan bahwa nilai probabilitas bersyarat adalah angka antara 0 dan 1. Semakin tinggi probabilitas bersyarat, semakin besar kemungkinan terjadinya peristiwa A ketika peristiwa B terjadi, tetapi semakin rendah probabilitas bersyarat, semakin kecil kemungkinan terjadinya peristiwa A. akan terjadi ketika peristiwa B terjadi.

Rumus Probabilitas Bersyarat

Peluang bersyarat kejadian A kejadian tertentu B sama dengan peluang perpotongan antara kejadian A dan kejadian B dibagi peluang kejadian B.

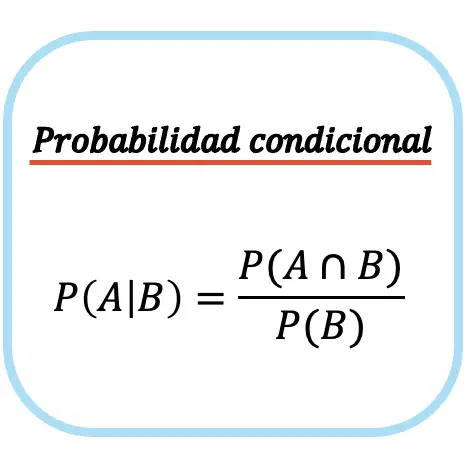
Perhatikan bahwa rumus probabilitas bersyarat (atau probabilitas bersyarat) hanya dapat digunakan jika probabilitas terjadinya peristiwa tak terkondisi bukan nol, yaitu P(B)≠0. Atau dengan kata lain apakah peristiwa B bisa saja terjadi.

Probabilitas bersyarat juga dapat dihitung dari inversnya, yaitu jika P(B|A) diketahui maka P(A|B) dapat ditentukan. Namun untuk melakukan ini Anda harus menerapkan teorema Bayes, Anda dapat melihat isi teorema ini di sini:

➤ Lihat: Apa teorema Bayes?

Contoh Probabilitas Bersyarat

Setelah kita melihat apa definisi dan rumus probabilitas bersyarat, kita akan menyelesaikan contoh probabilitas jenis ini langkah demi langkah untuk memahami maknanya sepenuhnya.

Setelah mengikuti ujian di kelas yang berjumlah 30 siswa, dilakukan pengumpulan data untuk mengetahui berapa banyak siswa yang belajar dan berapa yang lulus. Hasilnya disajikan pada tabel kontingensi berikut. Dari data yang dikumpulkan, hitung peluang bersyarat untuk lulus ujian jika Anda sudah belajar.

latihan probabilitas bersyarat terpecahkan

Untuk mendapatkan probabilitas bersyarat, kita harus menerapkan rumus yang kita lihat sebelumnya:

$P(\text{aprobado}|\text{estudiado})=\cfrac{P(\text{aprobado}\cap\text{estudiado})}{P(\text{estudiado})}$

Oleh karena itu, pertama-tama kita perlu mencari probabilitas bahwa seorang siswa belajar, belajar, dan lulus. Untuk mencari peluang seorang siswa belajar, kita cukup menggunakan aturan Laplace, yaitu kita membagi jumlah siswa yang belajar dengan jumlah observasi:

$P(\text{estudiado})=\cfrac{23}{30}=0,77$

Dan kita dapat mengetahui peluang seorang siswa belajar dan lulus pada waktu yang sama dari tabel kontingensi dengan membagi jumlah siswa yang belajar dan lulus dengan total:

$P(\text{aprobado}\cap \text{estudiado})=\cfrac{19}{30}=0,63$

Jadi, peluang seorang siswa lulus ujian jika ia telah belajar adalah:

$\begin{aligned}P(\text{aprobado}|\text{estudiado})&=\cfrac{P(\text{aprobado}\cap\text{estudiado})}{P(\text{estudiado})}\\ &=\cfrac{0,63}{0,77}\\[1.5ex] &=0,82\end{aligned}$

Probabilitas bersyarat dari kejadian dependen dan independen

Pada bagian ini kita akan melihat apa hubungan antara probabilitas bersyarat dan kejadian dependen dan independen (atau kejadian dependen dan independen). Sebab, meski berbeda konsep, kedua jenis kejadian ini terkait dengan probabilitas bersyarat.

Dua peristiwa (atau kejadian) bersifat independen jika probabilitas terjadinya tidak bergantung satu sama lain. Dalam kasus seperti ini, perpotongan antara dua kejadian setara dengan hasil kali probabilitas masing-masing kejadian secara terpisah. Oleh karena itu, rumus probabilitas bersyarat disederhanakan:

$P(A|B)=\cfrac{P(A\cap B)}{P(B)}=\cfrac{P(A)\cdot P(B)}{P(B)}=P(A)$

Singkatnya, jika kejadian A dan B saling bebas, maka peluang bersyarat dari kejadian A jika kejadian B sama persis dengan peluang terjadinya kejadian A.

Sebaliknya, jika dua kejadian saling bergantung, artinya peluang suatu kejadian bergantung pada peluang kejadian lainnya. Oleh karena itu, jika dua kejadian A dan B saling bergantung, peluang bersyarat kejadian A kejadian B tertentu berbeda dengan peluang terjadinya kejadian A.

$P(A|B)\neq P(A)$

Latihan probabilitas bersyarat yang terpecahkan

Latihan 1

Kita tahu bahwa di dalam kantong yang penuh dengan bola, separuhnya berwarna oranye dan separuhnya lagi berwarna hijau. Selain itu, sepertiga dari semua bola berwarna oranye dan sekaligus ditandai dengan tanda. Berapa probabilitas ketika Anda mengambil bola oranye, bola tersebut akan menerima sinyal?

Lihat solusinya

Untuk menyelesaikan latihan ini, kita harus menerapkan rumus probabilitas bersyarat, yaitu:

$P(\text{se\~nal}|\text{naranja})=\cfrac{P(\text{se\~nal}\cap\text{naranja})}{P(\text{naranja})}$

Rumusan masalah memberitahu kita bahwa setengah dari kantong itu adalah jeruk. Oleh karena itu, peluang teoritis terambilnya bola oranye adalah 50%.

$P(\text{naranja})=\cfrac{1}{2}=0,5$

Sebaliknya kita mengetahui bahwa sepertiga dari jumlah tersebut adalah bola jingga dan mempunyai sinyal, sehingga peluang terambilnya bola jingga yang mempunyai isyarat adalah:

$P(\text{se\~nal}\cap \text{naranja})=\cfrac{1}{3}=0,33$

Terakhir, kami mengganti probabilitas yang dihitung ke dalam rumus probabilitas bersyarat untuk menemukan nilainya:

$\begin{aligned}P(\text{se\~nal}|\text{naranja})&=\cfrac{P(\text{se\~nal}\cap\text{naranja})}{P(\text{naranja})}\\ &=\cfrac{0,33}{0,5}\\[1.5ex] &=0,66\end{aligned}$

Ringkasnya, peluang terambilnya bola dengan sinyal berwarna oranye adalah 66%.

Latihan 2

Jika kita mempunyai enam pulpen biru dan tiga pulpen hitam dalam sebuah kotak, hitung peluang terambilnya satu pulpen biru dan peluang terambilnya dua pulpen biru berturut-turut.

Lihat solusinya

Untuk menentukan peluang terambilnya pena biru satu kali, cukup gunakan hukum Laplace:

$P(\text{azul})=\cfrac{6}{6+3}=0,67$

Soal tersebut juga meminta kita mengetahui peluang terambilnya dua pena biru secara berurutan, yaitu peluang bersyarat terambilnya pena biru jika kita sudah mengambil pena biru sebelumnya.

Jika kita menggambar pena biru, kita mempunyai kasus yang kurang menguntungkan, tetapi totalnya juga ada satu pena yang lebih sedikit. Oleh karena itu, probabilitas bersyaratnya adalah:

$P(\text{azul}|\text{azul})=\cfrac{5}{8}=0,63$

Latihan 3

Berapa peluang bersyarat pelemparan sebuah dadu ke angka 4 jika pelemparan koin menghasilkan gambar?

Lihat solusinya

Untuk menyelesaikan latihan ini, Anda harus memperhitungkan teori probabilitas bersyarat, karena kejadian “mendapatkan angka 4 dengan melempar sebuah dadu” dan “mendapatkan kepala dengan melempar koin” adalah kejadian yang saling bebas. Oleh karena itu, rumus probabilitas bersyarat tidak perlu digunakan, tetapi persamaan berikut terpenuhi:

$P(\text{n\'umero 4}|\text{cara})=P(\text{n\'umero 4})$

Jadi, untuk mencari probabilitas bersyarat, cukup gunakan aturan Laplace:

$P(\text{n\'umero 4}|\text{cara})=P(\text{n\'umero 4})=\cfrac{1}{6}=0,167$

Latihan 4

Tahun keuangan 25 perusahaan di suatu negara dipelajari dan bagaimana harga saham mereka berubah tergantung pada hasil ekonomi tahun tersebut. Anda dapat melihat data yang dikumpulkan pada tabel kontingensi berikut:

Seberapa besar kemungkinan harga saham suatu perusahaan akan naik jika memperoleh keuntungan dalam setahun terakhir?

Lihat solusinya

Latihan ini menanyakan kepada kita tentang probabilitas bersyarat bahwa saham akan naik jika perusahaan telah mencapai hasil ekonomi yang positif. Jadi, untuk menghitung probabilitas ini, kita harus menggunakan rumus probabilitas bersyarat:

$P(\text{precio sube}|\text{beneficio})=\cfrac{P(\text{precio sube}\cap\text{beneficio})}{P(\text{beneficio})}$

Oleh karena itu, pertama-tama kita menghitung probabilitas suatu perusahaan memperoleh keuntungan dan, kedua, probabilitas suatu perusahaan memperoleh keuntungan ekonomis sambil menaikkan harga per sahamnya:

$P(\text{beneficio})=\cfrac{14}{25}=0,56$

$P(\text{precio sube}\cap\text{beneficio})=\cfrac{10}{25}=0,4$

Dan kemudian kita mengganti nilai yang ditemukan ke dalam rumus dan menghitung probabilitas bersyarat:

$\begin{aligned}P(\text{precio sube}|\text{beneficio})& =\cfrac{P(\text{precio sube}\cap\text{beneficio})}{P(\text{beneficio})}\\ &= \cfrac{0,4}{0,56}\\[1.5ex]& =0,71 \end{aligned}$

Sifat-sifat probabilitas bersyarat

Sifat-sifat probabilitas bersyarat, atau probabilitas bersyarat, adalah sebagai berikut:

Jumlah peluang bersyarat kejadian A kejadian tertentu B ditambah peluang bersyarat kejadian pelengkap A kejadian tertentu B sama dengan satu.

$P\bigl(A|B\bigr)+P\bigl(\overline{A}|B\bigr)=1$

Jika kejadian A merupakan himpunan bagian dari kejadian B, maka A akan selalu terjadi jika B benar. Jadi, peluang bersyarat dari kejadian A kejadian B tertentu dalam kasus ini adalah 1.

$B\subseteq A \ \longrightarrow \ P(A|B)=1$

Diberikan dua kejadian berbeda, persamaan berikut sehubungan dengan probabilitas bersyarat selalu berlaku:

$P\bigl(A\bigr)=P\bigl(A|B\bigr)\cdot P\bigl(B\bigr)+P\bigl(A|\overline{B}\bigl)\cdot P\bigl(\overline{B}\bigr)$

Tentang Penulis

Benjamin anderson

Halo, saya Benjamin, pensiunan profesor statistika yang menjadi guru Statorial yang berdedikasi. Dengan pengalaman dan keahlian yang luas di bidang statistika, saya ingin berbagi ilmu untuk memberdayakan mahasiswa melalui Statorials. Baca selengkapnya

Apa yang dimaksud dengan probabilitas bersyarat?

Rumus Probabilitas Bersyarat

Contoh Probabilitas Bersyarat

Probabilitas bersyarat dari kejadian dependen dan independen

Latihan probabilitas bersyarat yang terpecahkan

Latihan 1

Latihan 2

Latihan 3

Latihan 4

Sifat-sifat probabilitas bersyarat

Tentang Penulis

Benjamin anderson

Tambahkan komentar