Cara menghitung nilai yang diharapkan dari x^2
Untuk variabel acak yang dilambangkan dengan X, Anda dapat menggunakan rumus berikut untuk menghitung nilai yang diharapkan dari X 2 :
E(X 2 ) = Σx 2 * p(x)
Emas:
- Σ : Simbol yang berarti “jumlah”
- x : Nilai variabel acak
- p(x) : Probabilitas bahwa variabel acak mengambil nilai tertentu
Contoh berikut menunjukkan cara menggunakan rumus ini dalam praktik.
Contoh: Perhitungan nilai yang diharapkan dari X 2
Misalkan kita mempunyai tabel distribusi probabilitas berikut yang menggambarkan probabilitas suatu variabel acak,
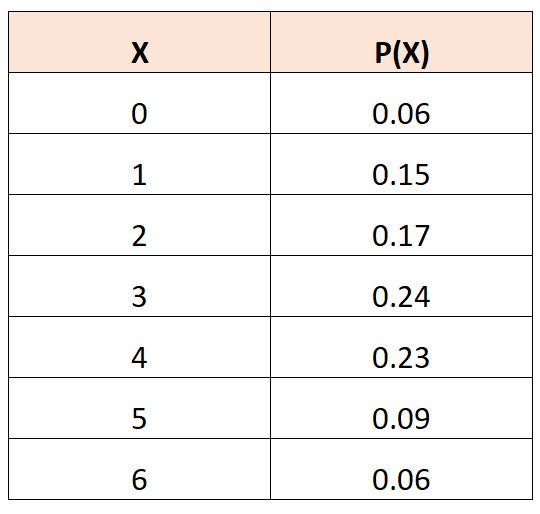
Untuk menghitung nilai yang diharapkan dari X 2 , kita dapat menggunakan rumus berikut:
E(X 2 ) = Σx 2 * p(x)
E(X 2 ) = (0) 2 *.06 + (1) 2 *.15 + (2) 2 *.17 + (3) 2 *.24 + (4) 2 *.23 + (5) 2 *.09 + (6) 2 *.06
E(X 2 ) = 0 + 0,15 + 0,68 + 2,16 + 3,68 + 2,25+ 2,16
E( X2 ) = 11,08
Nilai yang diharapkan dari X 2 adalah 11.08 .
Perhatikan bahwa variabel acak ini adalah variabel acak diskrit , artinya variabel tersebut hanya dapat mengambil sejumlah nilai yang terbatas.
Jika X adalah variabel acak kontinu , kita harus menggunakan rumus berikut untuk menghitung nilai yang diharapkan dari X 2 :
E(X 2 ) = ∫ x 2 f(x)dx
Emas:
- ∫: Simbol yang berarti “integrasi”
- f(x) : Pdf berlanjut untuk variabel acak
Saat menghitung nilai ekspektasi X2 untuk variabel acak kontinu, kami biasanya menggunakan perangkat lunak statistik karena penghitungan ini lebih sulit dilakukan secara manual.
Sumber daya tambahan
Tutorial berikut menjelaskan cara melakukan tugas umum lainnya dalam statistik:
Bagaimana mencari mean dari distribusi probabilitas
Bagaimana mencari simpangan baku dari suatu distribusi probabilitas
Bagaimana menemukan varians dari distribusi probabilitas
Tentang Penulis
Benjamin anderson
Halo, saya Benjamin, pensiunan profesor statistika yang menjadi guru Statorial yang berdedikasi. Dengan pengalaman dan keahlian yang luas di bidang statistika, saya ingin berbagi ilmu untuk memberdayakan mahasiswa melalui Statorials. Baca selengkapnya