Cara menghitung nilai yang diharapkan dari x^3
Untuk variabel acak yang dilambangkan dengan X, Anda dapat menggunakan rumus berikut untuk menghitung nilai yang diharapkan dari X 3 :
E(X 3 ) = Σx 3 * p(x)
Emas:
- Σ : Simbol yang berarti “jumlah”
- x : Nilai variabel acak
- p(x) : Probabilitas bahwa variabel acak mengambil nilai tertentu
Contoh berikut menunjukkan cara menggunakan rumus ini dalam praktik.
Contoh: Perhitungan nilai yang diharapkan dari X 3
Misalkan kita mempunyai tabel distribusi probabilitas berikut yang menggambarkan probabilitas suatu variabel acak,
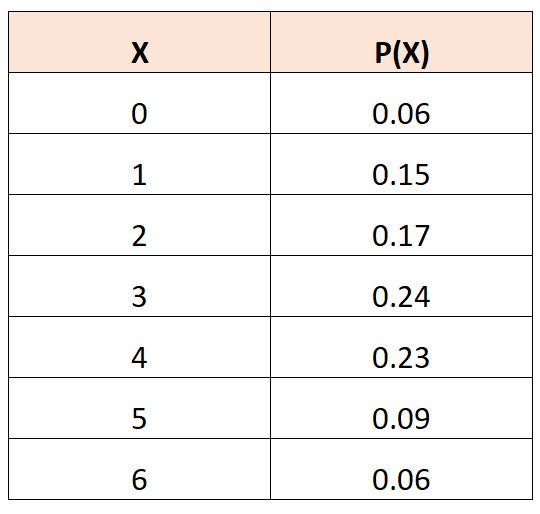
Untuk menghitung nilai yang diharapkan dari X 3 , kita dapat menggunakan rumus berikut:
E(X 3 ) = Σx 3 * p(x)
E(X 3 ) = (0) 3 *.06 + (1) 3 *.15 + (2) 3 *.17 + (3) 3 *.24 + (4) 3 *.23 + (5) 3 *.09 + (6) 3 *.06
E(X 3 ) = 0 + 0,15 + 0,1.36 + 6,48 + 14,72 + 11,25 + 12,96
E(X 3 ) = 45,596
Nilai yang diharapkan dari X 3 adalah 45,596 .
Perhatikan bahwa variabel acak ini adalah variabel acak diskrit , artinya variabel tersebut hanya dapat mengambil sejumlah nilai yang terbatas.
Jika X adalah variabel acak kontinu , kita harus menggunakan rumus berikut untuk menghitung nilai yang diharapkan dari X 3 :
E(X 3 ) = ∫ x 3 f(x)dx
Emas:
- ∫: Simbol yang berarti “integrasi”
- f(x) : Pdf berlanjut untuk variabel acak
Saat menghitung nilai yang diharapkan dari
Sumber daya tambahan
Tutorial berikut menjelaskan cara melakukan tugas umum lainnya dalam statistik:
Bagaimana mencari mean dari distribusi probabilitas
Bagaimana mencari simpangan baku dari suatu distribusi probabilitas
Bagaimana menemukan varians dari distribusi probabilitas