Cara melakukan regresi spline di r (dengan contoh)

Regresi spline adalah jenis regresi yang digunakan jika terdapat titik atau “simpul” yang pola datanya berubah secara tiba-tiba dan regresi linier serta regresi polinomial tidak cukup fleksibel untuk menyesuaikan data.

Contoh langkah demi langkah berikut menunjukkan cara melakukan regresi spline di R.

Langkah 1: Buat datanya

Pertama, mari kita buat kumpulan data di R dengan dua variabel dan buat plot sebar untuk memvisualisasikan hubungan antar variabel:

 #create data frame
df <- data. frame (x=1:20,
                 y=c(2, 4, 7, 9, 13, 15, 19, 16, 13, 10,
                     11, 14, 15, 15, 16, 15, 17, 19, 18, 20))

#view head of data frame
head(df)

  xy
1 1 2
2 2 4
3 3 7
4 4 9
5 5 13
6 6 15

#create scatterplot
plot(df$x, df$y, cex= 1.5 , pch= 19 )

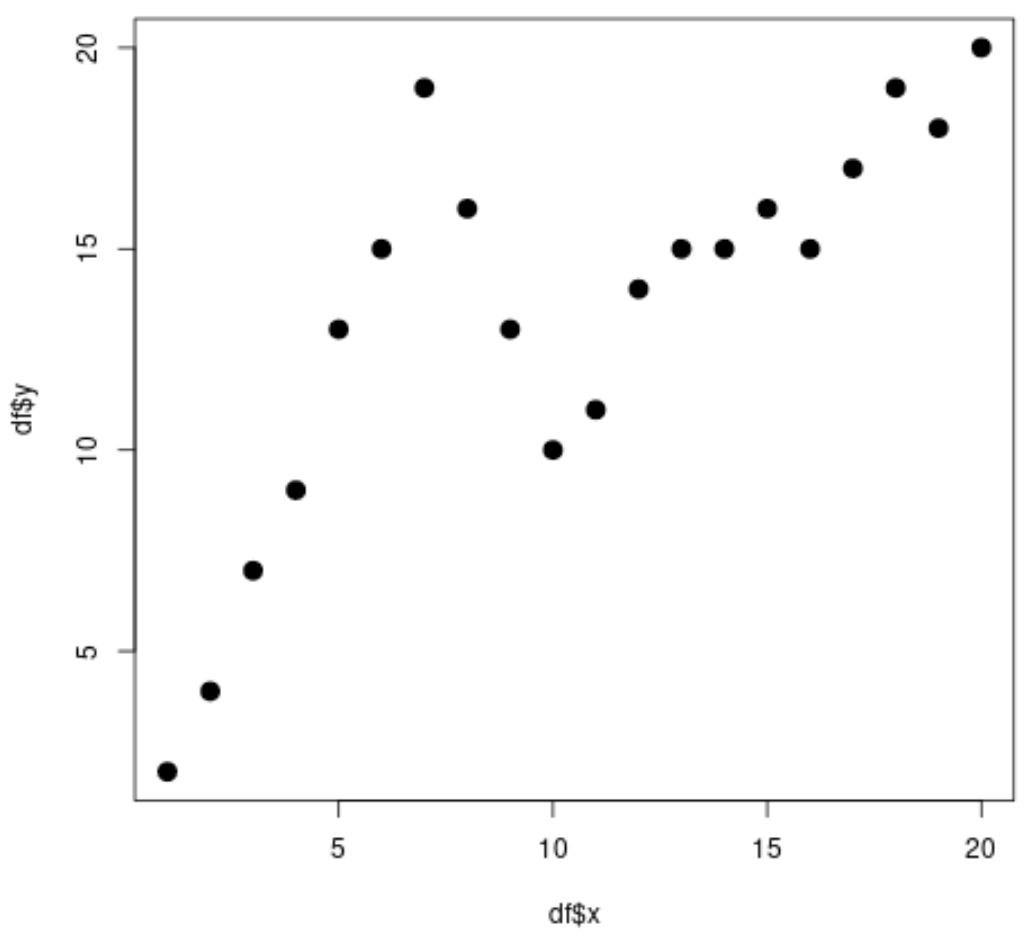
Jelas sekali hubungan antara x dan y adalah non-linier dan tampak ada dua titik atau “simpul” yang pola datanya berubah secara tiba-tiba pada x=7 dan x=10.

Langkah 2: Sesuaikan model regresi linier sederhana

Mari kita gunakan fungsi lm() untuk menyesuaikan model regresi linier sederhana dengan kumpulan data ini dan membuat plot yang sesuai dengan garis regresi pada plot sebar:

 #fit simple linear regression model
linear_fit <- lm(df$y ~ df$x)

#view model summary
summary(linear_fit)

Call:
lm(formula = df$y ~ df$x)

Residuals:
    Min 1Q Median 3Q Max 
-5.2143 -1.6327 -0.3534 0.6117 7.8789 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 6.5632 1.4643 4.482 0.000288 ***
df$x 0.6511 0.1222 5.327 4.6e-05 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.152 on 18 degrees of freedom
Multiple R-squared: 0.6118, Adjusted R-squared: 0.5903 
F-statistic: 28.37 on 1 and 18 DF, p-value: 4.603e-05

#create scatterplot
plot(df$x, df$y, cex= 1.5 , pch= 19 )

#add regression line to scatterplot
abline(linear_fit) 

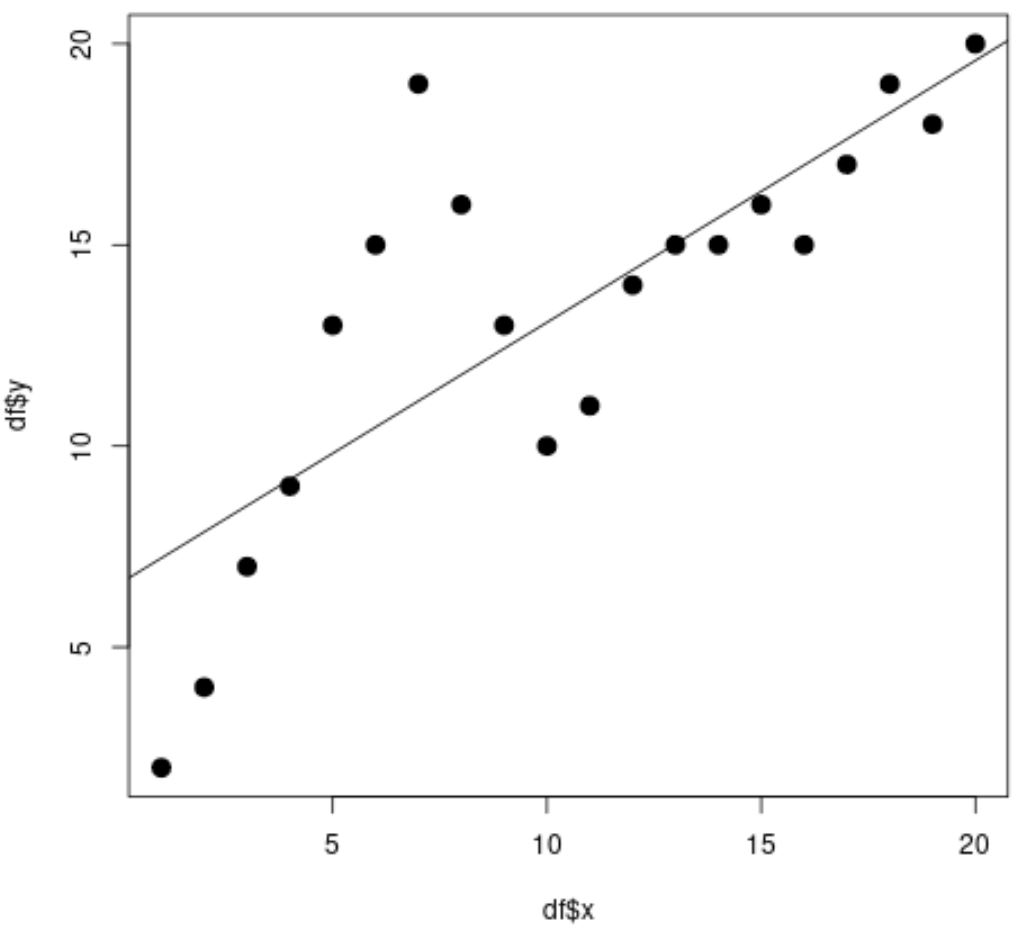
Dari scatterplot terlihat bahwa garis regresi linier sederhana tidak sesuai dengan data.

Dari hasil model juga terlihat nilai customized R-squared sebesar 0.5903 .

Kami akan membandingkannya dengan nilai R-kuadrat yang disesuaikan dari model spline.

Langkah 3: Sesuaikan model regresi spline

Selanjutnya, mari kita gunakan fungsi bs() dari paket splines untuk menyesuaikan model regresi spline dengan dua node, lalu plot model yang dipasang pada scatterplot:

 library (splines)

#fit spline regression model
spline_fit <- lm(df$y ~ bs(df$x, knots=c( 7 , 10 )))

#view summary of spline regression model
summary(spline_fit)

Call:
lm(formula = df$y ~ bs(df$x, knots = c(7, 10)))

Residuals:
     Min 1Q Median 3Q Max 
-2.84883 -0.94928 0.08675 0.78069 2.61073 

Coefficients:
                            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 2.073 1.451 1.429 0.175    
bs(df$x, knots = c(7, 10))1 2.173 3.247 0.669 0.514    
bs(df$x, knots = c(7, 10))2 19.737 2.205 8.949 3.63e-07 ***
bs(df$x, knots = c(7, 10))3 3.256 2.861 1.138 0.274    
bs(df$x, knots = c(7, 10))4 19.157 2.690 7.121 5.16e-06 ***
bs(df$x, knots = c(7, 10))5 16.771 1.999 8.391 7.83e-07 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.568 on 14 degrees of freedom
Multiple R-squared: 0.9253, Adjusted R-squared: 0.8987 
F-statistic: 34.7 on 5 and 14 DF, p-value: 2.081e-07

#calculate predictions using spline regression model
x_lim <- range(df$x)
x_grid <- seq(x_lim[ 1 ], x_lim[ 2 ])
preds <- predict(spline_fit, newdata=list(x=x_grid))

#create scatter plot with spline regression predictions
plot(df$x, df$y, cex= 1.5 , pch= 19 )
lines(x_grid, preds) 

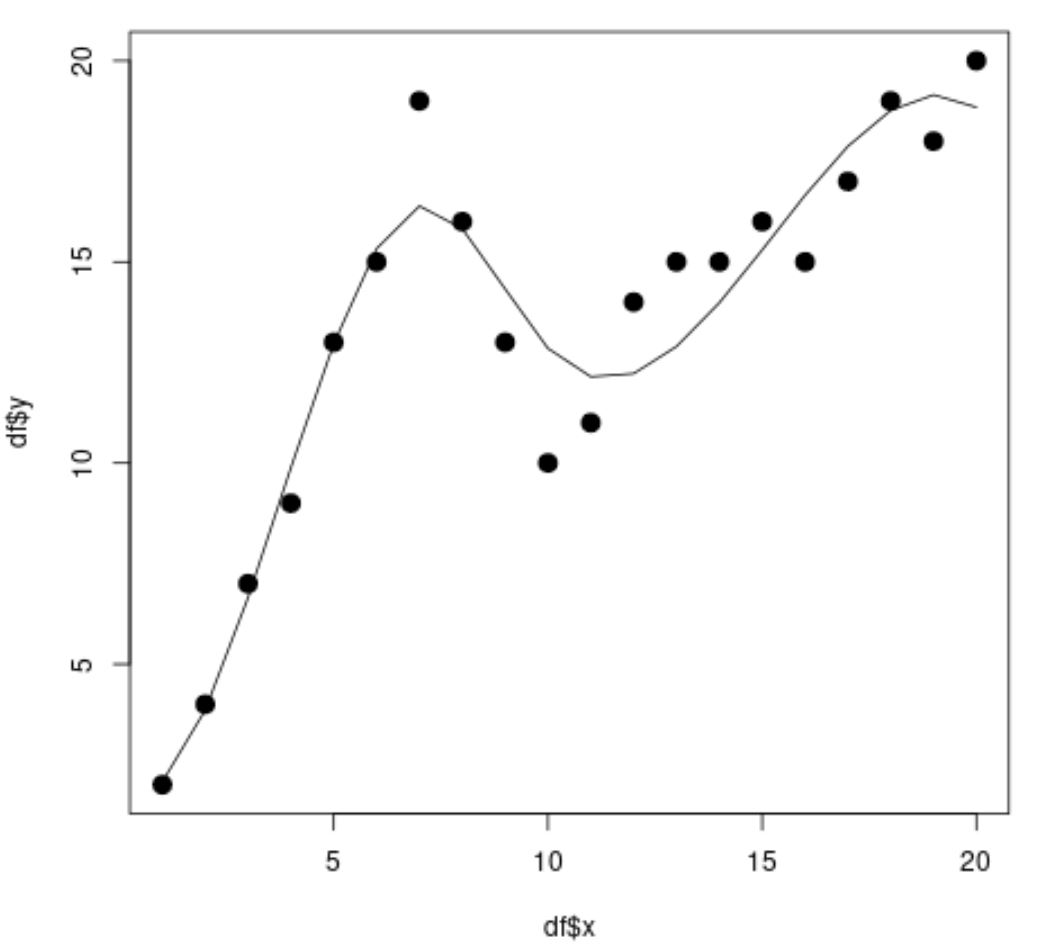
Dari scatterplot terlihat bahwa model regresi spline mampu menyesuaikan data dengan cukup baik.

Dari hasil model juga terlihat nilai customized R-squared sebesar 0.8987 .

Nilai R-kuadrat yang disesuaikan untuk model ini jauh lebih tinggi dibandingkan model regresi linier sederhana, yang menunjukkan bahwa model regresi spline mampu menyesuaikan data dengan lebih baik.

Perhatikan bahwa untuk contoh ini kita telah memilih bahwa node terletak di x=7 dan x=10.

Dalam praktiknya, Anda harus memilih sendiri lokasi node berdasarkan pola perubahan pada data dan berdasarkan keahlian domain Anda.

Sumber daya tambahan

Tutorial berikut menjelaskan cara melakukan tugas umum lainnya di R:

Cara melakukan regresi linier berganda di R
Bagaimana melakukan regresi eksponensial di R
Bagaimana melakukan regresi kuadrat terkecil tertimbang di R