Distribusi hipergeometri

Oleh Benjamin anderson Agustus 6, 2023 Kemungkinan 0 Komentar

Pada artikel ini kami menjelaskan apa itu distribusi hipergeometri dan bagaimana probabilitas dihitung dengan jenis distribusi ini. Anda dapat menemukan rumus distribusi hipergeometri secara online, apa saja karakteristiknya, serta kalkulator untuk menghitung probabilitas distribusi hipergeometri.

Apa yang dimaksud dengan distribusi hipergeometri?

Distribusi hipergeometri adalah distribusi probabilitas yang menggambarkan jumlah kasus yang berhasil dalam ekstraksi acak tanpa penggantian n elemen dari suatu populasi.

Artinya, distribusi hipergeometri digunakan untuk menghitung probabilitas memperoleh x keberhasilan ketika mengekstraksi n elemen dari suatu populasi tanpa mengganti salah satu elemen tersebut.

Distribusi hipergeometri memiliki tiga parameter:

N : banyaknya elemen dalam populasi (N = 0, 1, 2,…).
K : adalah jumlah kasus keberhasilan maksimum (K = 0, 1, 2,…,N). Karena dalam distribusi hipergeometri suatu elemen hanya dapat dianggap sebagai “berhasil” atau “gagal”, NK adalah jumlah maksimum kasus kegagalan.
n : adalah jumlah pengambilan tanpa penggantian yang dilakukan.

$X \sim HG(N,K,n)$

Misalnya, variabel acak diskrit X yang mempunyai distribusi hipergeometri dengan parameter N=8, K=5 dan n=3 didefinisikan sebagai berikut:

$X \sim HG(8,5,3)$

Rumus distribusi hipergeometri

Rumus distribusi hipergeometri adalah hasil kali bilangan kombinatorial K atas x dengan bilangan kombinatorial NK atas nx dibagi bilangan kombinatorial N atas n .

Dimana N adalah ukuran populasi, K adalah jumlah total kasus yang menguntungkan, n adalah jumlah ekstraksi tanpa pengembalian dan x adalah jumlah kasus yang menguntungkan dimana probabilitas terjadinya harus dihitung.

👉 Anda dapat menggunakan kalkulator di bawah ini untuk menghitung peluang suatu kejadian suatu variabel yang mengikuti distribusi hipergeometri.

Contoh distribusi hipergeometri

Setelah kita melihat pengertian dan rumus distribusi hipergeometri, sekarang kita akan menyelesaikan contoh langkah demi langkah agar Anda mengetahui cara menghitung peluang distribusi hipergeometri.

Di dalam sebuah tas kita masukkan 20 bola biru dan 30 bola merah, jadi totalnya ada 50 bola di dalam tas. Jika kita mengambil 12 bola tanpa mengganti satupun, tentukan peluang terambilnya 4 bola biru.

Hal pertama yang perlu kita lakukan untuk menyelesaikan latihan ini adalah mengidentifikasi parameter distribusi hipergeometri. Dalam hal ini, jumlah total elemen dalam populasi adalah 50 ( N =50), jumlah maksimum kasus yang menguntungkan adalah 20 ( K =20), dan diambil 12 bola ( n =12).

$\left.\begin{array}{c}N=50\\[2ex]K=20\\[2ex]n=12\end{array}\right\} \longrightarrow \ X\sim HG(50,20,12)$

Kami ingin menghitung peluang terambilnya 4 bola biru ( x =4), jadi kami menerapkan rumus distribusi hipergeometri, mengganti variabel dengan nilainya yang sesuai dan melakukan perhitungan:

$P\bigl[X=x\bigr]=\cfrac{\begin{pmatrix}K\\x\end{pmatrix}\begin{pmatrix}N-K\\n-x\end{pmatrix}}{\begin{pmatrix}N\\n\end{pmatrix}}$

$\begin{aligned}P\bigl[X=4\bigr]&=\cfrac{\begin{pmatrix}20\\4\end{pmatrix}\begin{pmatrix}50-20\\12-4\end{pmatrix}}{\begin{pmatrix}50\\12\end{pmatrix}} \\[1.5ex]&=\cfrac{\begin{pmatrix}20\\4\end{pmatrix}\begin{pmatrix}30\\8\end{pmatrix}}{\begin{pmatrix}50\\12\end{pmatrix}} \\[1.5ex]&=0,2336 \end{aligned}$

Kalkulator Distribusi Hipergeometri

Masukkan parameter distribusi hipergeometri ke dalam kalkulator online berikut untuk menghitung peluang terjadinya peristiwa yang diinginkan.

Ingatlah bahwa N adalah ukuran populasi, K adalah jumlah total kasus yang menguntungkan, n adalah ukuran sampel, dan x adalah nilai yang ingin kita cari kemungkinan terjadinya kasus tersebut.

Ciri-ciri distribusi hipergeometri

Distribusi hipergeometri mempunyai sifat sebagai berikut:

Nilai yang diharapkan dari distribusi hipergeometri sama dengan jumlah elemen dalam sampel dikalikan dengan jumlah kasus yang menguntungkan dibagi dengan jumlah elemen dalam populasi.

$E[X]=\cfrac{n\cdot K}{N}$

Modus distribusi hipergeometri adalah nilai yang dibulatkan ke bawah dari hasil kali n+1 dikali K+1 dibagi N+2 .

$\displaystyle M=\Bigg\lfloor \frac{(n+1)(K+1)}{N+2}\Bigg\rfloor$

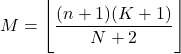
Varians dari distribusi hipergeometri dapat diperoleh dengan menggunakan ekspresi berikut:

$\displaystyle Var[X]=\cfrac{nK}{N}\left(\frac{N-K}{N}\right)\left(\frac{N-n}{N-1}\right)$

Fungsi pembangkit momen dari distribusi hipergeometri adalah sebagai berikut:

$\cfrac{{N-K \choose n} \scriptstyle{\,_2F_1(-n, -K; N - K-n+1; e^{t}) } }{{N \choose n}}$

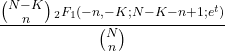
Fungsi karakteristik dari distribusi hipergeometri adalah sebagai berikut:

$\cfrac{{N-K \choose n} \scriptstyle{\,_2F_1(-n, -K; N - K - n + 1; e^{it}) }}{{N \choose n}}$

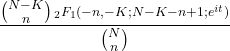
Peluang terjadinya sejumlah kejadian tertentu dapat dihitung dari peluang kejadian sebelumnya dengan menggunakan rekursif untuk distribusi hipergeometri:

$P[X=x+1]=\cfrac{(K-x)(n-x)}{(x+1)(N-K-n+x-1)}\cdot P[X=x]$

Distribusi hipergeometri dan distribusi binomial

Perbedaan distribusi hipergeometri dan distribusi binomial adalah penggantiannya. Distribusi hipergeometri digunakan ketika pengambilan tidak diganti, namun dalam distribusi binomial pengambilan diganti.

Misalnya, jika kita mengambil lima kartu secara acak dalam satu tumpukan dan kita ingin menghitung peluang terambilnya kartu tertentu, jika kita tidak mengganti setiap kartu yang kita ambil, kita harus menggunakan distribusi hipergeometri untuk melakukan perhitungannya. Namun jika pada saat mengeluarkan kartu kita memasangnya kembali sebelum melakukan ekstraksi berikutnya, maka kita harus menggunakan distribusi binomial untuk menghitung probabilitasnya.

Jika bilangan N besar, rasio n/N kecil, dan jumlah kasus menguntungkan yang diinginkan sangat kecil, kita dapat menggunakan distribusi hipergeometri sebagai perkiraan distribusi binomial. Namun, saya tidak merekomendasikannya karena hasilnya tidak dapat diandalkan dan, terlebih lagi, lebih mudah menghitung probabilitas dengan hukum binomial dibandingkan dengan hukum hipergeometri.

Tentang Penulis

Benjamin anderson

Halo, saya Benjamin, pensiunan profesor statistika yang menjadi guru Statorial yang berdedikasi. Dengan pengalaman dan keahlian yang luas di bidang statistika, saya ingin berbagi ilmu untuk memberdayakan mahasiswa melalui Statorials. Baca selengkapnya