Cara menghitung aic di sas (dengan contoh)

Kriteria Informasi Akaike (AIC) adalah metrik yang digunakan untuk membandingkan kesesuaian model regresi berganda.

Ini dihitung sebagai berikut:

AIC = 2K – 2 ln (L)

Emas:

• K : Jumlah parameter model. Nilai default K adalah 2, sehingga model dengan hanya satu variabel prediktor akan memiliki nilai K 2+1 = 3.
• ln (L) : Log-likelihood model. Kebanyakan perangkat lunak statistik dapat menghitung nilai ini secara otomatis untuk Anda.

AIC dirancang untuk menemukan model yang menjelaskan variasi data paling banyak, sekaligus memberi sanksi pada model yang menggunakan jumlah parameter berlebihan.

Setelah Anda memasang beberapa model regresi, Anda dapat membandingkan nilai AIC setiap model. Semakin rendah AIC maka semakin cocok model tersebut.

Contoh berikut menunjukkan cara menghitung AIC untuk model regresi yang berbeda di SAS.

Contoh: Cara menghitung AIC di SAS

Misalkan kita ingin menyesuaikan tiga model regresi linier berganda yang berbeda untuk memprediksi nilai ujian yang akan dicapai siswa di suatu kelas.

Berikut variabel prediktor yang akan kami gunakan di setiap model:

• Variabel prediktor dalam model 1: jam yang dihabiskan untuk belajar
• Variabel prediktor dalam model 2: ujian praktek yang lalu
• Variabel prediktor dalam Model 3: jam yang dihabiskan untuk belajar dan ujian praktik yang diambil

Pertama, kita akan menggunakan kode berikut untuk membuat kumpulan data yang berisi informasi ini untuk 20 siswa:

 /*create dataset*/
data exam_data;
    input hours prep_exams score;
    datalines ;
1 1 76
2 3 78
2 3 85
4 5 88
2 2 72
1 2 69
5 1 94
4 1 94
2 0 88
4 3 92
4 4 90
3 3 75
6 2 96
5 4 90
3 4 82
4 4 85
6 5 99
2 1 83
1 0 62
2 1 76
;
run ;

Selanjutnya, kita akan menggunakan proc reg untuk menyesuaikan masing-masing model regresi ini dan kita akan menggunakan pernyataan seleksi=adjrsq sse aic untuk menghitung nilai AIC untuk setiap model:

 /*fit multiple linear regression models and calculate AIC for each model*/
proc reg data =exam_data;
    model score = hours prep_exams / selection=adjrsq sse aic;
run ; 

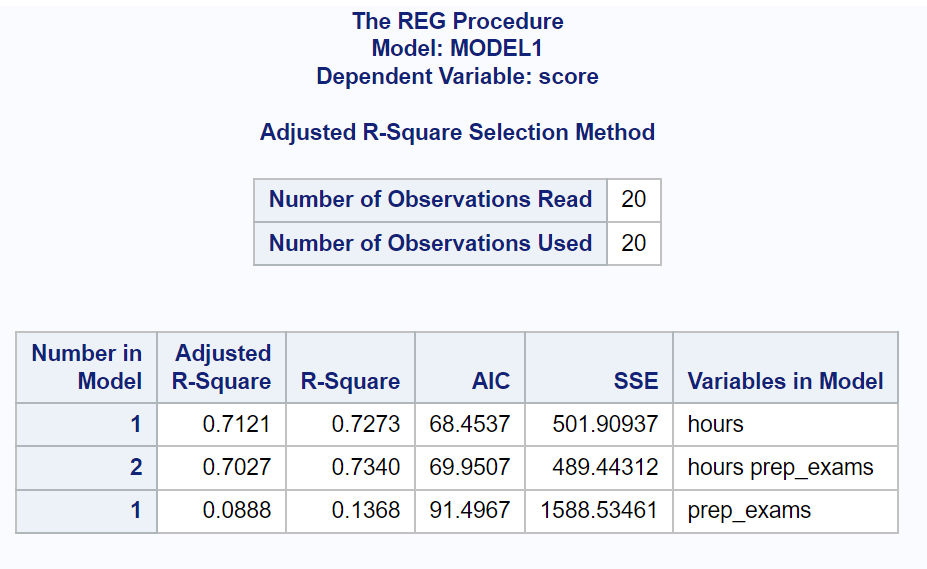
Dari hasilnya kita dapat melihat nilai AIC untuk masing-masing model:

• AIC dengan jam sebagai variabel prediktor: 68.4537
• AIC dengan jam kerja dan ujian sebagai variabel prediktor: 69,9507
• AIC dengan ujian sebagai variabel prediktif: 91,4967

Model dengan nilai AIC terendah adalah model yang hanya memuat jam sebagai variabel prediktor.

Oleh karena itu, kami menyatakan bahwa model berikut paling sesuai dengan data:

Skor = β ₀ + β ₁ (jam belajar)

Setelah kami mengidentifikasi model ini sebagai yang terbaik, kami dapat menyesuaikannya dan menganalisis hasilnya, termasuk nilai R-kuadrat dan koefisien beta, untuk menentukan hubungan yang tepat antara jam belajar dan nilai siswa. ‘ujian akhir.

Sumber daya tambahan

Tutorial berikut menjelaskan cara melakukan tugas umum lainnya di SAS:

Cara melakukan regresi linier sederhana di SAS
Cara melakukan regresi linier berganda di SAS
Cara menghitung R-kuadrat di SAS
Cara menghitung RMSE di SAS