Cara menggunakan fitdistr() di r agar sesuai dengan distribusi

Anda dapat menggunakan fungsi fitdistr() dari paket MASS di R untuk memperkirakan parameter distribusi dengan memaksimalkan fungsi kemungkinan.

Fungsi ini menggunakan sintaks dasar berikut:

fitdistr(x, kesenangan padat, …)

Emas:

• x : Vektor numerik yang mewakili nilai distribusi
• dosefun : distribusi untuk memperkirakan parameternya

Perhatikan bahwa argumen dosefun menerima nama distribusi potensial berikut: beta , cauchy , chi-square , eksponensial , gamma , geometrik , lognormal , logistik , binomial negatif , normal , Poisson , t , dan Weibull .

Contoh berikut menunjukkan cara menggunakan fungsi fitdistr() dalam praktiknya.

Contoh: Cara menggunakan fungsi fitdistr() untuk menyesuaikan distribusi di R

Misalkan kita menggunakan fungsi rnorm() di R untuk menghasilkan vektor 200 nilai yang mengikuti distribusi normal:

 #make this example reproducible
set. seeds (1)

#generate sample of 200 observations that follows normal dist with mean=10 and sd=3
data <- rnorm(200, mean=10, sd=3)

#view first 6 observations in sample
head(data)

[1] 8.120639 10.550930 7.493114 14.785842 10.988523 7.538595

Kita dapat menggunakan fungsi hist() untuk membuat histogram guna memvisualisasikan distribusi nilai data:

 hist(data, col=' steelblue ')

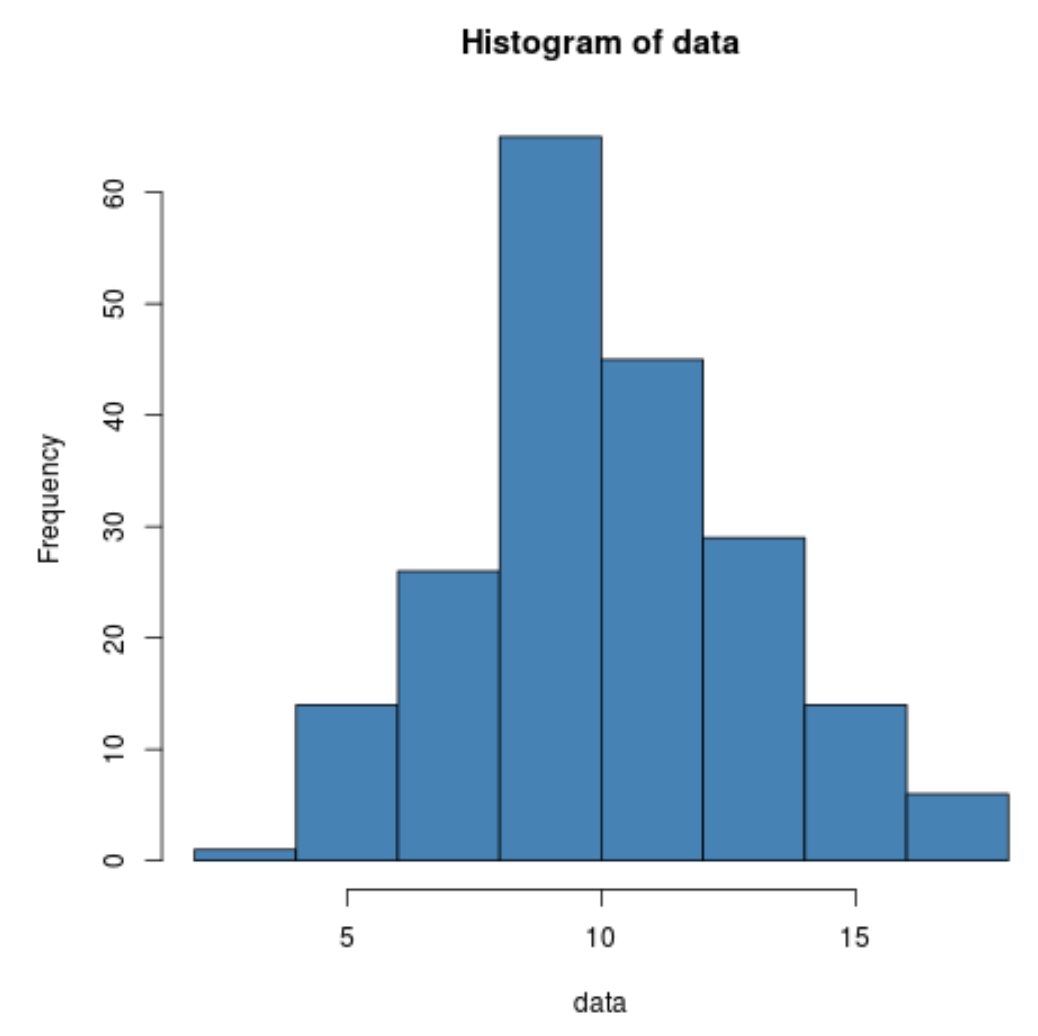
Kita dapat melihat bahwa datanya memang tampak terdistribusi normal.

Kita kemudian dapat menggunakan fungsi fitdistr() untuk memperkirakan parameter distribusi ini:

 library (MASS)

#estimate parameters of distribution
fitdistr(data, “ normal ”)

      mean sd    
  10.1066189 2.7803148 
 (0.1965979) (0.1390157)

Fungsi fitdistr() memperkirakan vektor nilai mengikuti distribusi normal dengan mean 10.1066189 dan standar deviasi 2.7803148 .

Nilai-nilai ini seharusnya tidak mengherankan karena kami menghasilkan data menggunakan fungsi rnorm() dengan nilai rata-rata 10 dan deviasi standar 3.

Sumber daya tambahan

Tutorial berikut menjelaskan cara melakukan tugas umum lainnya di R:

Cara memplot distribusi normal di R
Cara menghasilkan distribusi normal di R
Cara melakukan uji normalitas Shapiro-Wilk di R