Cara melakukan tes white di sas

Uji White digunakan untuk mengetahui apakah terdapat heteroskedastisitas dalam suatu model regresi.

Heteroskedastisitas mengacu pada penyebaran residu yang tidak merata pada berbagai tingkat variabel respons dalam model regresi, yang melanggar salah satu asumsi utama regresi linier bahwa residu tersebar secara merata di setiap tingkat variabel respons.

Tutorial ini menjelaskan cara melakukan uji White di SAS untuk menentukan apakah heteroskedastisitas merupakan masalah dalam model regresi tertentu.

Contoh: Tes putih di SAS

Misalkan kita ingin menyesuaikan model regresi linier berganda yang menggunakan jumlah jam yang dihabiskan untuk belajar dan jumlah ujian praktik yang diambil untuk memprediksi nilai ujian akhir siswa:

Nilai ujian = β ₀ + β ₁ (jam) + β ₂ (persiapan ujian)

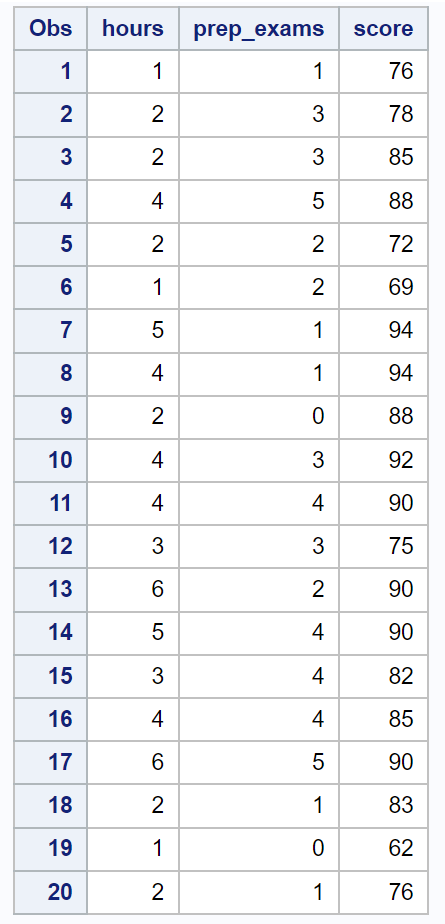
Pertama, kita akan menggunakan kode berikut untuk membuat kumpulan data yang berisi informasi ini untuk 20 siswa:

 /*create dataset*/
data exam_data;
    input hours prep_exams score;
    datalines ;
1 1 76
2 3 78
2 3 85
4 5 88
2 2 72
1 2 69
5 1 94
4 1 94
2 0 88
4 3 92
4 4 90
3 3 75
6 2 90
5 4 90
3 4 82
4 4 85
6 5 90
2 1 83
1 0 62
2 1 76
;
run ;

/*view dataset*/
proc print data =exam_data; 

Selanjutnya, kita akan menggunakan proc reg agar sesuai dengan model regresi linier berganda ini serta opsi spesifikasi untuk melakukan uji White untuk heteroskedastisitas:

 /*fit regression model and perform White's test*/
proc reg data =exam_data;
    model score = hours prep_exams / spec ;
run ;
quit ; 

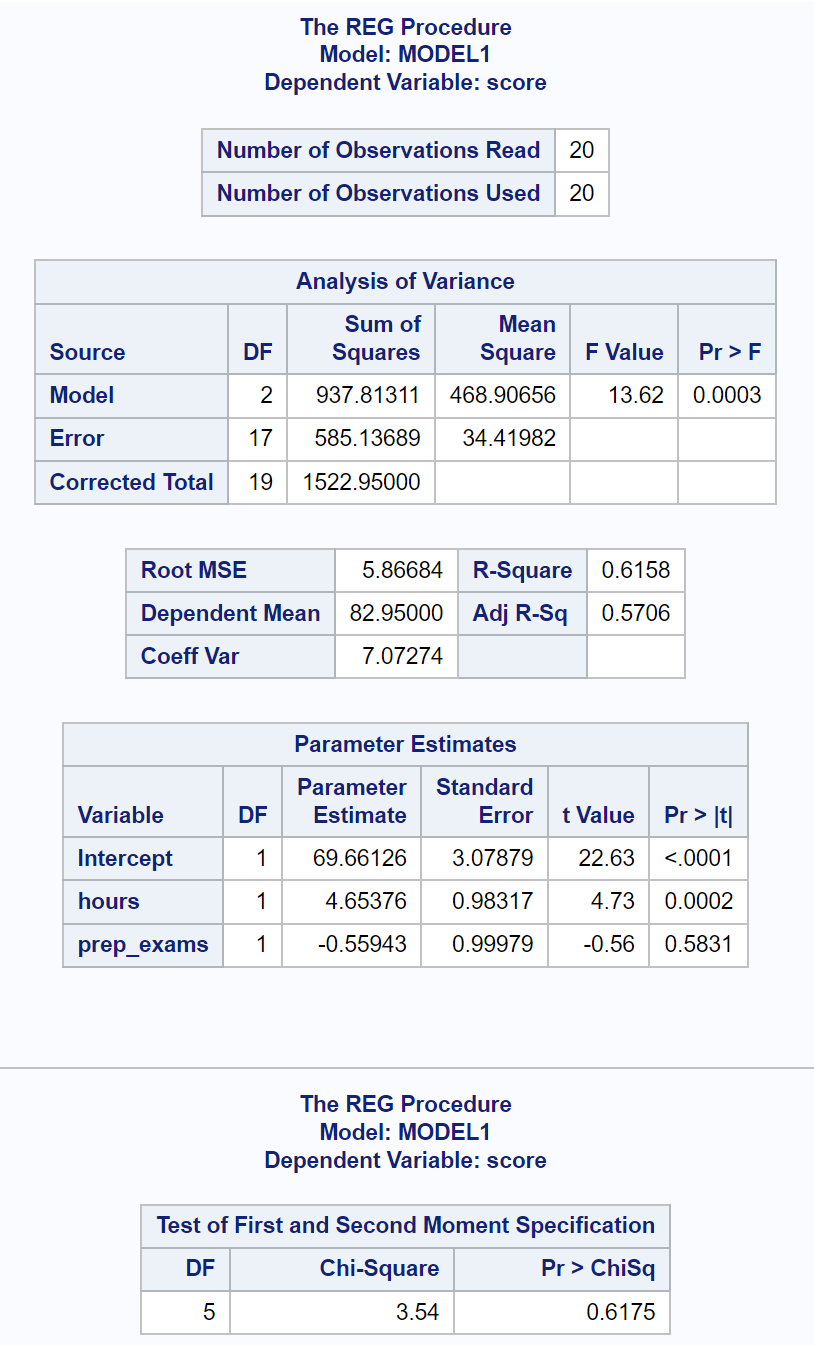
Tabel hasil terakhir menunjukkan hasil tes White.

Dari tabel ini, kita dapat melihat bahwa statistik uji Chi-kuadrat adalah 3,54 dan nilai p yang sesuai adalah 0,6175 .

Tes White menggunakan hipotesis nol dan hipotesis alternatif berikut:

• Null (H ₀ ) : Tidak terdapat heteroskedastisitas.
• Alternatif ( _HA ): Ada heteroskedastisitas.

Karena nilai p tidak kurang dari 0,05, kita gagal menolak hipotesis nol.

Artinya kita tidak mempunyai cukup bukti untuk menyatakan adanya heteroskedastisitas dalam model regresi.

Oleh karena itu, kesalahan standar estimasi koefisien dalam tabel ringkasan regresi dapat diinterpretasikan dengan aman.

Apa yang harus dilakukan selanjutnya

Jika Anda gagal menolak hipotesis nol uji White, maka tidak terjadi heteroskedastisitas dan Anda dapat melanjutkan untuk menginterpretasikan hasil regresi awal.

Namun jika hipotesis nol ditolak, berarti terdapat heteroskedastisitas pada data. Dalam hal ini, kesalahan standar yang ditampilkan dalam tabel keluaran regresi mungkin tidak dapat diandalkan.

Ada beberapa cara umum untuk mengatasi masalah ini, antara lain:

1. Transformasikan variabel respon. Anda dapat mencoba melakukan transformasi pada variabel respon.

Misalnya, Anda dapat menggunakan variabel respons log alih-alih variabel respons asli.

Secara umum , mengambil log dari variabel respon merupakan cara yang efektif untuk menghilangkan heteroskedastisitas.

Transformasi umum lainnya adalah dengan menggunakan akar kuadrat dari variabel respon.

2. Gunakan regresi tertimbang. Jenis regresi ini memberikan bobot pada setiap titik data berdasarkan varians dari nilai yang dipasang.

Hal ini memberikan bobot kecil pada titik data yang memiliki varian lebih tinggi, sehingga mengurangi kuadrat residunya.

Jika bobot yang digunakan sesuai maka masalah heteroskedastisitas dapat dihilangkan.