Panduan lengkap: cara menafsirkan hasil anova di sas

ANOVA satu arah digunakan untuk menentukan apakah terdapat perbedaan yang signifikan secara statistik antara rata-rata tiga atau lebih kelompok independen.

Contoh berikut menunjukkan bagaimana menginterpretasikan hasil ANOVA satu arah di SAS.

Contoh: Menafsirkan hasil ANOVA dalam SAS

Misalkan seorang peneliti merekrut 30 siswa untuk berpartisipasi dalam suatu penelitian. Siswa ditugaskan secara acak untuk menggunakan salah satu dari tiga metode belajar untuk mempersiapkan ujian.

Hasil ujian untuk setiap siswa ditunjukkan di bawah ini:

Kita dapat menggunakan kode berikut untuk membuat dataset ini di SAS:

 /*create dataset*/
data my_data;
    input Method $Score;
    datalines ;
At 78
At 81
At 82
At 82
At 85
At 88
At 88
At 90
B 81
B 83
B 83
B85
B 86
B 88
B90
B91
C 84
C 88
C 88
C 89
C 90
C 93
C 95
C 98
;
run ;

Selanjutnya, kita akan menggunakan proc ANOVA untuk melakukan ANOVA satu arah:

 /*perform one-way ANOVA*/
proc ANOVA data =my_data;
    classMethod ;
    modelScore = Method;
    means Method / tukey cldiff ;
run ;

Catatan : Kami menggunakan pernyataan mean bersama dengan opsi tukey dan cldiff untuk menentukan bahwa uji post-hoc Tukey harus dilakukan (dengan interval kepercayaan) jika nilai p keseluruhan dari ANOVA satu arah signifikan secara statistik.

Pertama, kita akan melihat tabel ANOVA pada hasilnya:

Berikut cara menafsirkan setiap nilai dalam output:

Model DF: Derajat kebebasan untuk metode variabel. Ini dihitung sebagai #grup -1. Dalam hal ini terdapat 3 metode belajar yang berbeda, sehingga nilainya adalah: 3-1 = 2 .

Kesalahan DF: derajat kebebasan residu. Ini dihitung sebagai #total observasi – #kelompok. Dalam hal ini terdapat 24 observasi dan 3 kelompok, sehingga nilainya adalah: 24-3 = 21 .

Total yang dikoreksi : jumlah model DF dan kesalahan DF. Nilai ini adalah 2 + 21 = 23 .

Model Sum of Squares: Jumlah kuadrat yang terkait dengan metode variabel. Nilai ini adalah 175.583 .

Kesalahan Jumlah Kuadrat: Jumlah kuadrat yang terkait dengan sisa atau “kesalahan”. Nilai ini adalah 350,25 .

Total Jumlah Kuadrat yang Dikoreksi : Jumlah model SS dan kesalahan SS. Nilai ini adalah 525.833 .

Model kuadrat rata-rata: jumlah rata-rata kuadrat yang terkait dengan metode ini . Ini dihitung sebagai model SS / model DF, atau 175.583 / 2 = 87.79 .

Kesalahan kuadrat rata-rata: jumlah rata-rata kuadrat yang terkait dengan residu. Ini dihitung sebagai SS Error / DF Error, yaitu 350.25 / 21 = 16.68 .

Nilai F : Statistik F keseluruhan model ANOVA. Ini dihitung sebagai model mean square/mean square error, atau 87.79/16.68 = 5.26 .

Pr >F: Nilai p yang dikaitkan dengan statistik F dengan pembilang df = 2 dan penyebut df = 21. Dalam hal ini, nilai p adalah 0,0140 .

Nilai yang paling penting dalam kumpulan hasil adalah nilai p, karena nilai ini memberi tahu kita jika terdapat perbedaan yang signifikan dalam nilai rata-rata antara ketiga kelompok.

Ingatlah bahwa ANOVA satu arah menggunakan hipotesis nol dan hipotesis alternatif berikut:

• H ₀ (hipotesis nol): semua mean kelompok adalah sama.
• H _A (hipotesis alternatif): Setidaknya rata-rata satu kelompok berbeda dari yang lain.

Karena nilai p dalam tabel ANOVA kami (0,0140) kurang dari 0,05, kami menolak hipotesis nol.

Artinya, kami memiliki cukup bukti untuk mengatakan bahwa rata-rata nilai ujian di ketiga metode belajar tidak sama.

Untuk menentukan dengan pasti mean grup mana yang berbeda, kita perlu mengacu pada tabel hasil akhir yang menunjukkan hasil tes post-hoc Tukey:

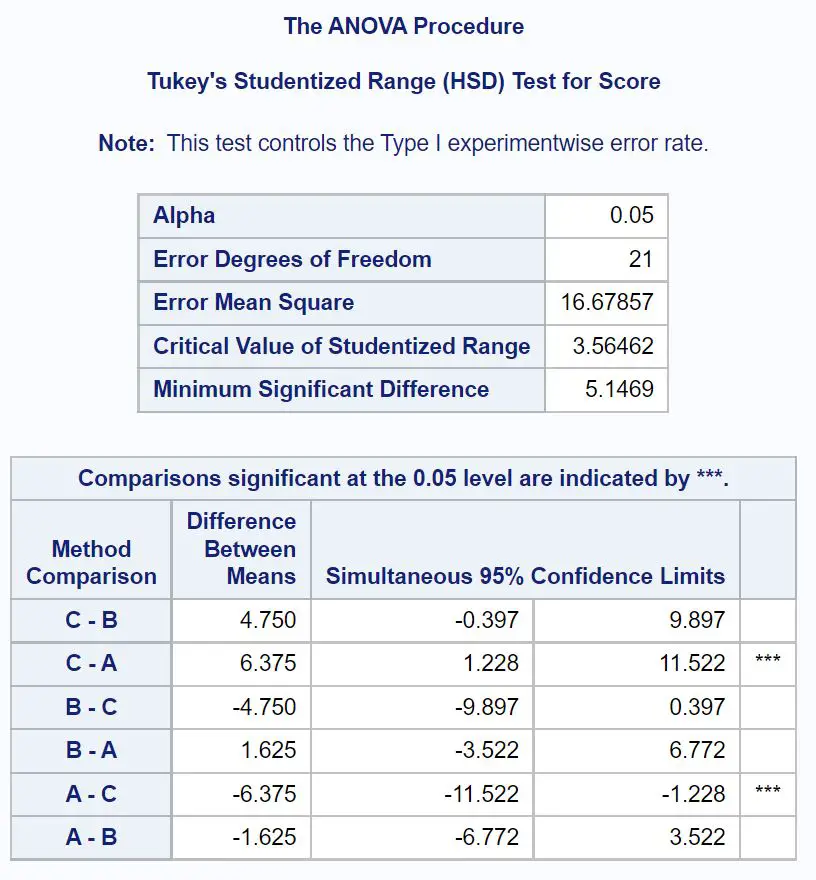
Untuk mengetahui mean grup mana yang berbeda, kita perlu melihat perbandingan berpasangan mana yang memiliki bintang ( *** ) di sebelahnya.

Tabel tersebut menunjukkan bahwa terdapat perbedaan yang signifikan secara statistik pada rata-rata nilai ujian antara Grup A dan Grup C.

Secara spesifik, rata-rata selisih nilai ujian antara Kelompok C dan Kelompok A adalah 6,375 .

Interval kepercayaan 95% untuk perbedaan rata-rata adalah [1.228, 11.522] .

Tidak ada perbedaan yang signifikan secara statistik antara rata-rata kelompok lainnya.

Sumber daya tambahan

Tutorial berikut memberikan informasi tambahan tentang model ANOVA:

Panduan Menggunakan Pengujian Post-Hoc dengan ANOVA
Cara melakukan ANOVA satu arah di SAS
Cara melakukan ANOVA dua arah di SAS