Cara menghitung skewness & kurtosis di sas
Dalam statistik, skewness dan kurtosis adalah dua cara untuk mengukur bentuk suatu distribusi.
Skewness mengukur asimetri suatu distribusi.
- Kemiringan negatif menunjukkan bahwa ekor distribusi berada di sisi kiri.
- Kemiringan positif menunjukkan bahwa ekornya berada di sisi kanan distribusi.
- Nilai nol menunjukkan tidak adanya asimetri dalam distribusi, artinya distribusi tersebut simetris sempurna.
Kurtosis mengukur apakah suatu distribusi berekor berat atau ringan dibandingkan dengan distribusi normal .
- Kurtosis distribusi normal adalah 0.
- Jika suatu distribusi tertentu mempunyai kurtosis kurang dari 0, maka dikatakan distribusi tersebut playkurtic , artinya distribusi tersebut cenderung menghasilkan outlier yang lebih sedikit dan tidak ekstrim dibandingkan distribusi normal.
- Jika suatu distribusi mempunyai kurtosis lebih besar dari 0 maka dikatakan leptokurtik , artinya cenderung menghasilkan lebih banyak outlier dibandingkan distribusi normal.
Untuk menghitung skewness dan kurtosis variabel di SAS, Anda dapat menggunakan pernyataan SKEWNESS dan KURTOSIS di PROC MEANS .
Contoh berikut menunjukkan cara menggunakan instruksi ini dalam praktik.
Contoh: Menghitung Skewness dan Kurtosis di SAS
Misalkan kita memiliki kumpulan data berikut di SAS yang berisi informasi tentang berbagai pemain bola basket:
/*create dataset*/ data my_data; input team $points assists; datalines ; At 10 2 At 17 5 At 17 6 At 18 3 At 15 0 B 10 2 B 14 5 B 13 4 B 29 0 B 25 2 C 12 1 C 30 1 C 34 3 C 12 4 C 11 7 ; run ; /*view dataset*/ proc print data =my_data;
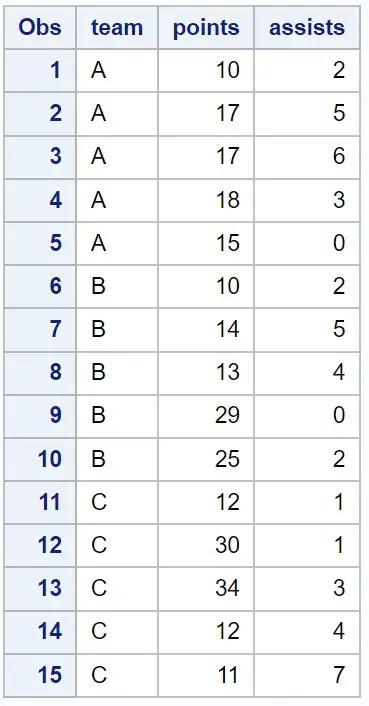
Kita dapat menggunakan PROC MEANS dengan pernyataan SKEWNESS dan KURTOSIS untuk menghitung skewness dan kurtosis setiap variabel numerik dalam kumpulan data:
/*calculate skewness and kurtosis for each numeric variable*/ proc means data =my_data SKEWNESS KURTOSIS ; run ;
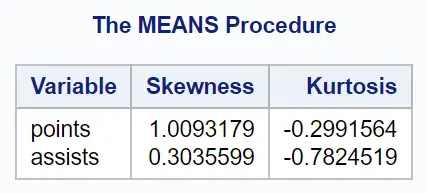
Tabel keluaran menampilkan nilai skewness dan kurtosis untuk setiap variabel numerik dalam dataset:
(1) poin
- Variabel points memiliki skewness sebesar 1.009 . Karena nilai ini lebih besar dari 0, berarti ekornya berada di sisi kanan distribusi.
- Variabel poin memiliki kurtosis sebesar -0.299 . Karena nilai ini kurang dari 0, berarti distribusi tersebut memiliki outlier yang sedikit lebih sedikit dan nilai yang kurang ekstrem dibandingkan distribusi normal.
(2) bantuan
- Variabel assist mempunyai skewness sebesar 0.304 . Karena nilai ini lebih besar dari 0, berarti ekornya berada di sisi kanan distribusi.
- Variabel support mempunyai kurtosis sebesar -0.782 . Karena nilai ini kurang dari 0, berarti distribusi tersebut memiliki outlier yang lebih sedikit dan nilai yang tidak terlalu ekstrem dibandingkan distribusi normal.
Untuk memvisualisasikan distribusi nilai setiap variabel numerik dalam kumpulan data, Anda dapat menggunakan PROC UNIVARIATE untuk membuat histogram untuk variabel titik dan bantuan:
/*create histograms for points and assists variables*/
proc univariate data =my_data;
var points assists;
histogram points assists;
run ;
Ini menghasilkan histogram berikut untuk variabel poin :
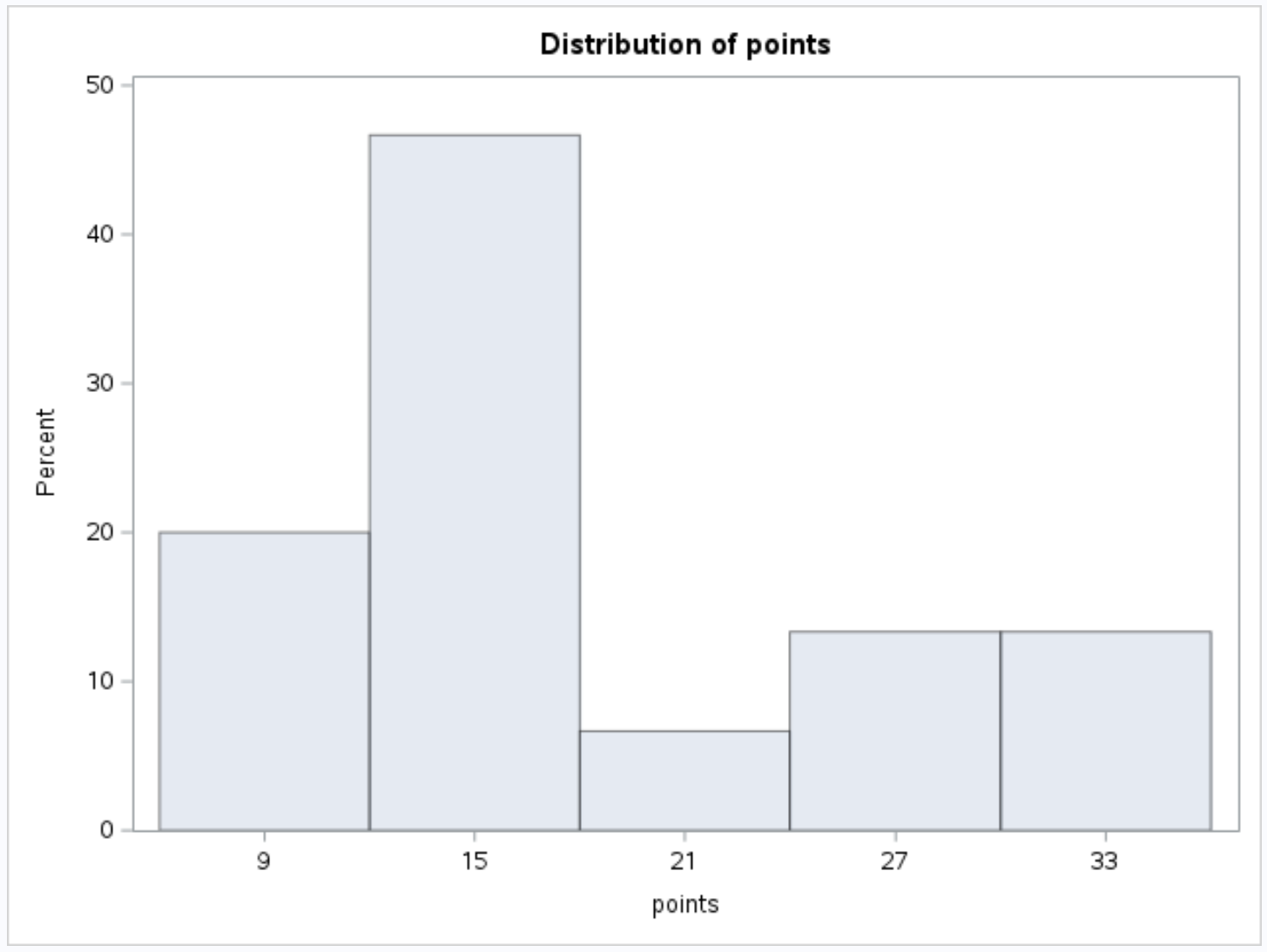
Dan berikut histogram untuk variabel bantuannya :
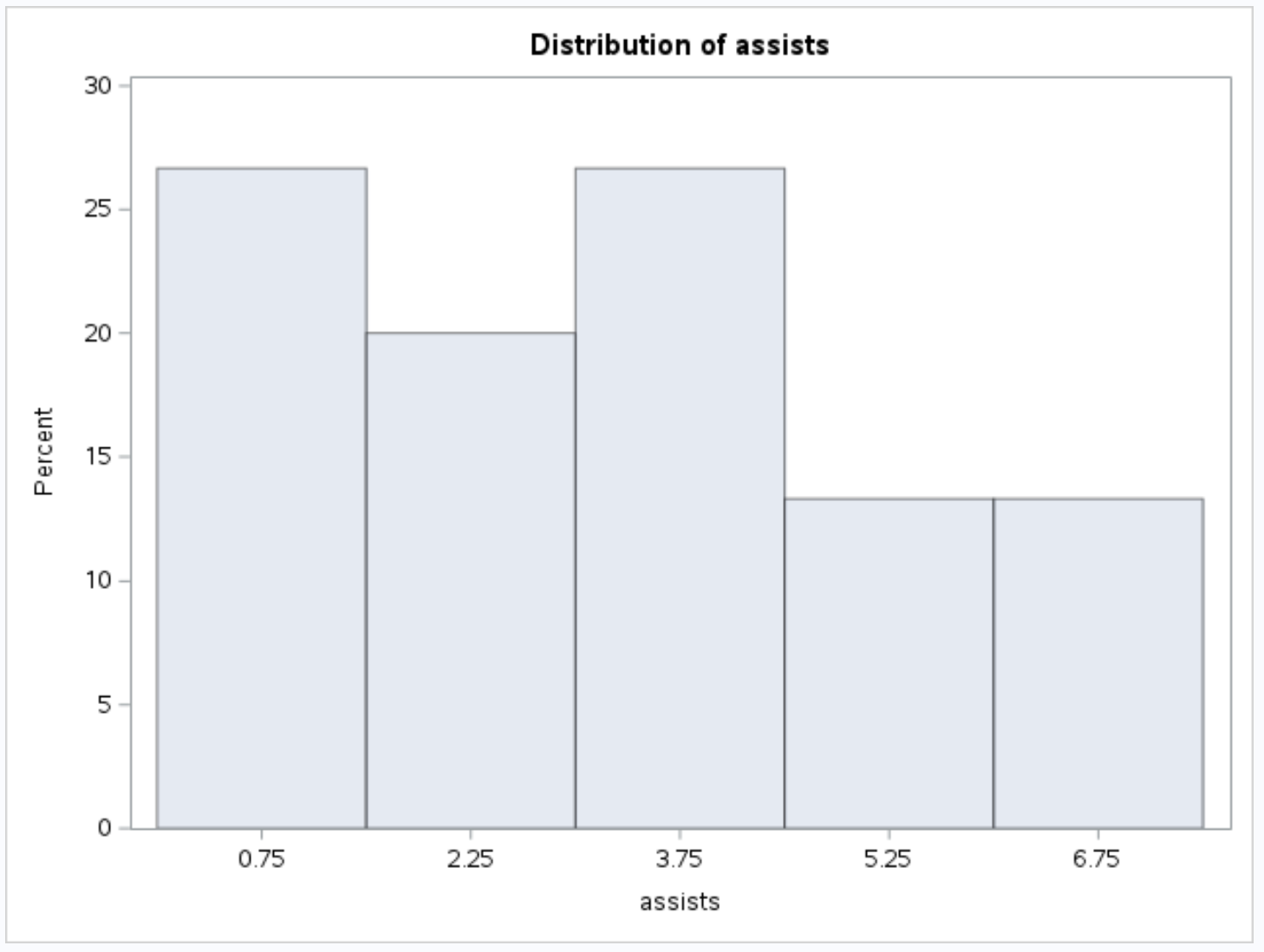
Sumber daya tambahan
Tutorial berikut menjelaskan cara melakukan tugas umum lainnya di SAS:
Cara menghitung statistik deskriptif di SAS
Cara membuat tabel frekuensi di SAS
Cara menghitung persentil di SAS
Cara Membuat PivotTable di SAS