Bagaimana melakukan analisis komponen utama di sas

Analisis komponen utama (PCA) adalah teknik pembelajaran mesin tanpa pengawasan yang berupaya menemukan komponen utama – kombinasi linier variabel prediktor – yang menjelaskan sebagian besar variasi dalam kumpulan data.

Cara paling sederhana untuk melakukan PCA di SAS adalah dengan menggunakan pernyataan PROC PRINCOMP , yang menggunakan sintaks dasar berikut:

 proc princomp data =my_data out =out_data outstat =stats;
    var var1 var2 var3;
run ;

Inilah yang dilakukan setiap instruksi:

• data : Nama kumpulan data yang akan digunakan untuk PCA
• out : Nama kumpulan data yang akan dibuat yang berisi semua data asli ditambah skor komponen utama
• outstat : Menentukan bahwa kumpulan data harus dibuat berisi rata-rata, deviasi standar, koefisien korelasi, nilai eigen, dan vektor eigen.
• var : variabel yang akan digunakan untuk PCA dari kumpulan data masukan.

Contoh langkah demi langkah berikut menunjukkan cara menggunakan pernyataan PROC PRINCOMP dalam praktiknya untuk melakukan analisis komponen utama di SAS.

Langkah 1: Buat kumpulan data

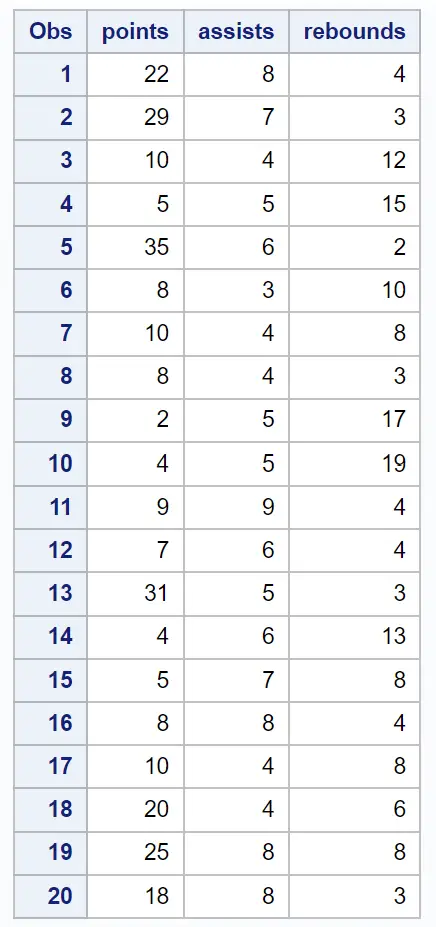
Misalkan kita memiliki kumpulan data berikut yang berisi berbagai informasi tentang 20 pemain bola basket:

 /*create dataset*/
data my_data;
    input points assists rebounds;
    datalines ;
22 8 4
29 7 3
10 4 12
5 5 15
35 6 2
8 3 10
10 4 8
8 4 3
2 5 17
4 5 19
9 9 4
7 6 4
31 5 3
4 6 13
5 7 8
8 8 4
10 4 8
20 4 6
25 8 8
18 8 3
;
run ;

/*view dataset*/
proc print data =my_data; 

Langkah 2: Lakukan analisis komponen utama

Kita dapat menggunakan pernyataan PROC PRINCOMP untuk melakukan analisis komponen utama menggunakan variabel points , assists , dan bouncing pada dataset:

 /*perform principal components analysis*/
proc princomp data =my_data out =out_data outstat =stats;
    var points assists rebounds;
run ;

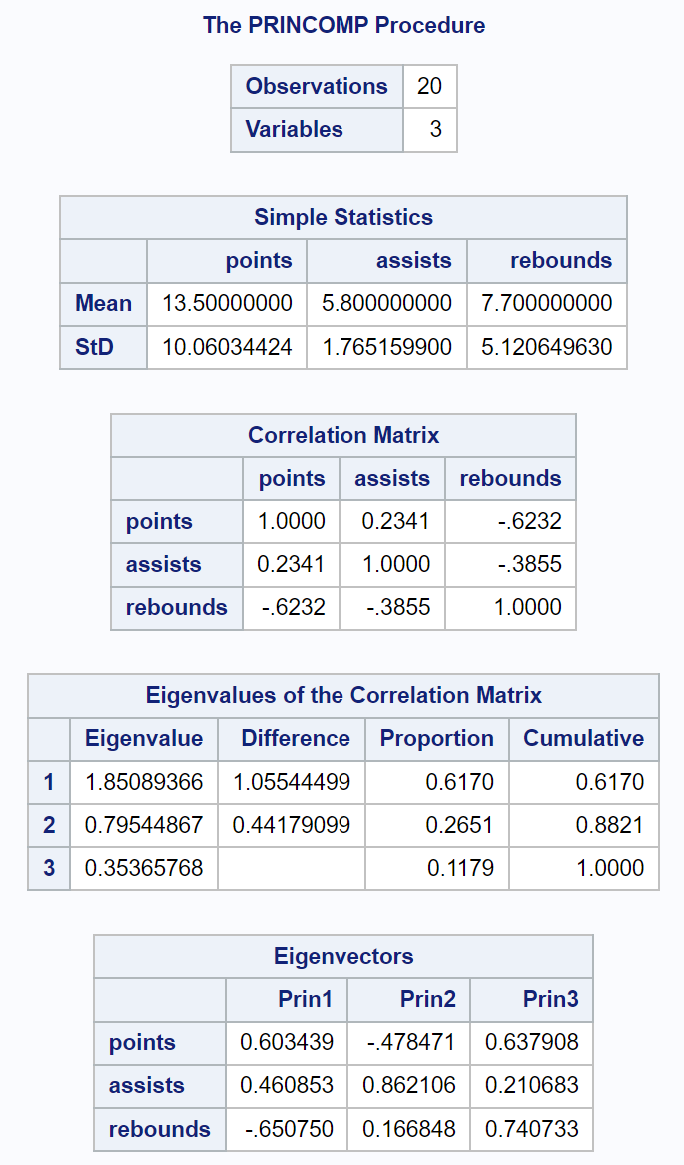
Bagian pertama keluaran menampilkan berbagai statistik deskriptif, termasuk mean dan deviasi standar setiap variabel masukan, matriks korelasi, serta nilai nilai eigen dan vektor eigen:

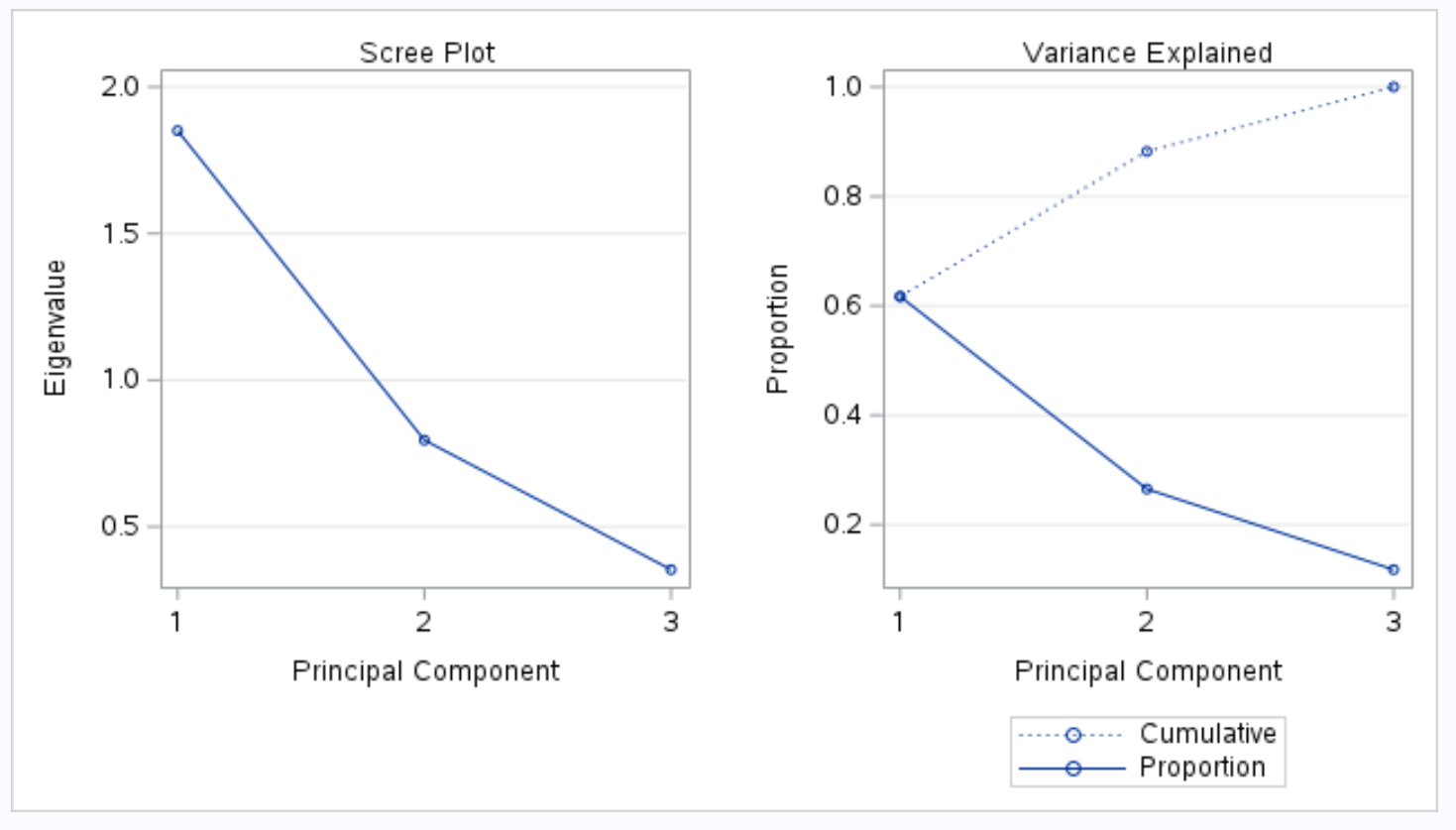
Bagian selanjutnya dari output menampilkan plot scree dan plot varians yang dijelaskan :

Saat kita melakukan PCA, sering kali kita ingin memahami berapa persentase total variasi kumpulan data yang dapat dijelaskan oleh setiap komponen utama.

Tabel yang dihasilkan berjudul Nilai Eigen Matriks Korelasi memungkinkan kita melihat dengan tepat berapa persentase total variasi yang dijelaskan oleh setiap komponen utama:

• Komponen utama pertama menjelaskan 61,7% dari total variasi kumpulan data.
• Komponen utama kedua menjelaskan 26,51% dari total variasi dataset.
• Komponen utama ketiga menjelaskan 11,79% dari total variasi dataset.

Perhatikan bahwa semua persentase berjumlah 100%.

Plot bertajuk Variance Dijelaskan kemudian memungkinkan kita memvisualisasikan nilai-nilai tersebut.

Sumbu x menampilkan komponen utama dan sumbu y menampilkan persentase varians total yang dijelaskan oleh masing-masing komponen utama.

Langkah 3: Buat biplot untuk memvisualisasikan hasilnya

Untuk memvisualisasikan hasil PCA pada suatu dataset tertentu, kita dapat membuat biplot , yaitu plot yang menampilkan setiap observasi dalam suatu dataset pada bidang yang dibentuk oleh dua komponen utama pertama.

Kita dapat menggunakan sintaks berikut di SAS untuk membuat biplot:

 /*create dataset with column called obs to represent row numbers of original data*/
data biplot_data;
   set out_data;
   obs=_n_;
run ;

/*create biplot using values from first two principal components*/
proc sgplot data =biplot_data;
    scatter x =Prin1 y =Prin2 / datalabel =obs;
run ; 

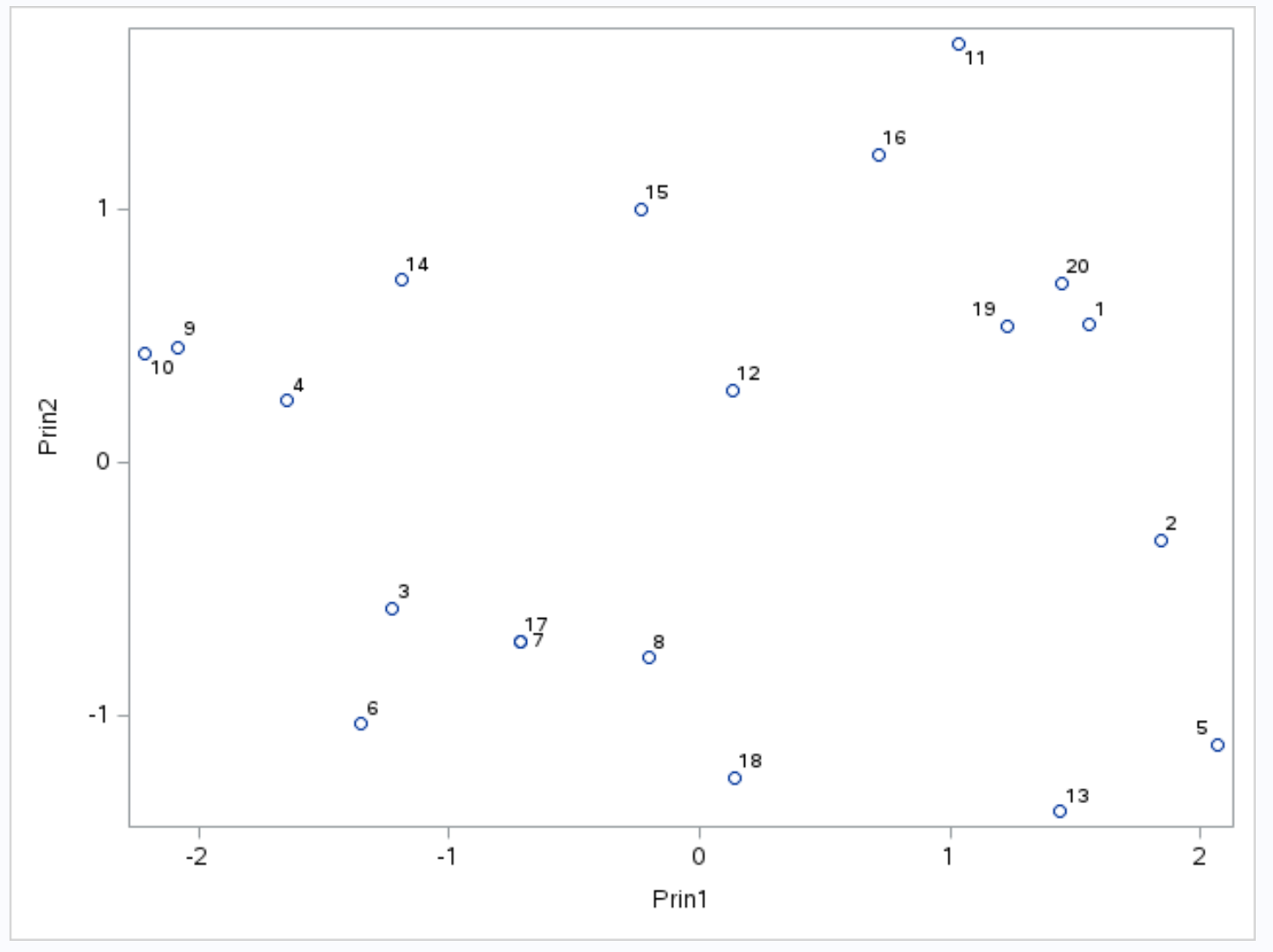
Sumbu x menampilkan komponen utama pertama, sumbu y menampilkan komponen utama kedua, dan observasi individual dari kumpulan data ditampilkan di dalam grafik sebagai lingkaran kecil.

Pengamatan yang berdampingan pada grafik memiliki nilai yang sama untuk ketiga variabel poin , assist , dan rebound .

Misalnya, di paling kiri grafik, kita dapat melihat bahwa observasi #9 dan #10 sangat berdekatan satu sama lain.

Jika kita mengacu pada dataset asli, kita dapat melihat nilai observasi berikut:

• Pengamatan n°9 : 2 poin, 5 assist, 17 rebound
• Pengamatan #10 : 4 poin, 5 assist, 19 rebound

Nilai-nilai tersebut serupa untuk masing-masing dari ketiga variabel, yang menjelaskan mengapa pengamatan ini sangat dekat satu sama lain pada biplot.

Kita juga melihat pada tabel hasil yang berjudul Nilai Eigen Matriks Korelasi bahwa dua komponen utama pertama menyumbang 88,21% dari total variasi dalam kumpulan data.

Karena persentase ini sangat tinggi, maka valid untuk menganalisis pengamatan mana dalam biplot yang berdekatan satu sama lain, karena dua komponen utama yang membentuk biplot bertanggung jawab atas hampir seluruh variasi dalam kumpulan data.

Sumber daya tambahan

Tutorial berikut menjelaskan cara melakukan tugas umum lainnya di SAS:

Cara melakukan regresi linier sederhana di SAS
Cara melakukan regresi linier berganda di SAS
Cara melakukan regresi logistik di SAS