Cara membuat interval keyakinan menggunakan distribusi f

Untuk menentukan apakah varians dua populasi sama, kita dapat menghitung rasio varians σ ² ₁ / σ ² ₂ , dimana σ ² ₁ adalah varians populasi 1 dan σ ² ₂ adalah varians populasi 2.

Untuk memperkirakan rasio varians populasi sebenarnya, kita biasanya mengambil sampel acak sederhana dari setiap populasi dan menghitung rasio varians sampel, s ₁ ² / s ₂ ² , dimana s ₁ ² dan s ₂ ² adalah varians sampel untuk sampel 1 dan sampel . 2, masing-masing.

Pengujian ini mengasumsikan bahwa s ₁ ² dan s ₂ ² dihitung dari sampel independen berukuran n ₁ dan n ₂ , keduanya berasal dari populasi yang berdistribusi normal.

Semakin jauh rasio ini dari satu, semakin kuat bukti adanya ketimpangan varians dalam populasi.

Interval kepercayaan (1-α)100% untuk σ ² ₁ / σ ² ₂ didefinisikan sebagai:

(s ₁ ² / s ₂ ² ) * F _{n 1 -1, n 2 -1, α/2} ≤ σ ² ₁ / σ ² ₂ ≤ (s ₁ ² / s ₂ ² ) * F _{n 2 -1, n 1 -1, α/2}

dimana F _{n 2 -1, n 1 -1, α/2} dan F _{n 1 -1, n 2 -1, α/2}   adalah nilai kritis distribusi F untuk tingkat signifikansi α yang dipilih.

Contoh berikut mengilustrasikan cara membuat interval kepercayaan untuk σ ² ₁ / σ ² ₂ menggunakan tiga metode berbeda:

• Dengan tangan
• Gunakan Microsoft Excel
• Penggunaan perangkat lunak statistik R

Untuk setiap contoh berikut, kami akan menggunakan informasi berikut:

• = 0,05
• n ₁ = 16
• _n2 = 11
• s ₁ ² =28,2
• s ₂ ² = 19,3

Membuat interval kepercayaan secara manual

Untuk menghitung selang kepercayaan secara manual untuk σ ² ₁ / σ ² ₂ , kita cukup memasukkan angka-angka yang kita miliki ke dalam rumus selang kepercayaan:

(s ₁ ² / s ₂ ² ) * F _{n1-1, n2-1,α/2} ≤ σ ² ₁ / σ ² ₂ ≤ (s ₁ ² / s ₂ ² ) * F _{n2-1, n1-1, α/2}

Satu-satunya angka yang kami lewatkan adalah nilai kritisnya. Untungnya, kita dapat menemukan nilai-nilai kritis ini di tabel distribusi F :

F _{n2-1, n1-1, α/2} = F _{10, 15, 0,025} = 3,0602

F _{n1-1, n2-1, α/2} = 1/ F _{15, 10, 0,025} = 1 / 3,5217 = 0,2839

(Klik untuk memperbesar tabel)

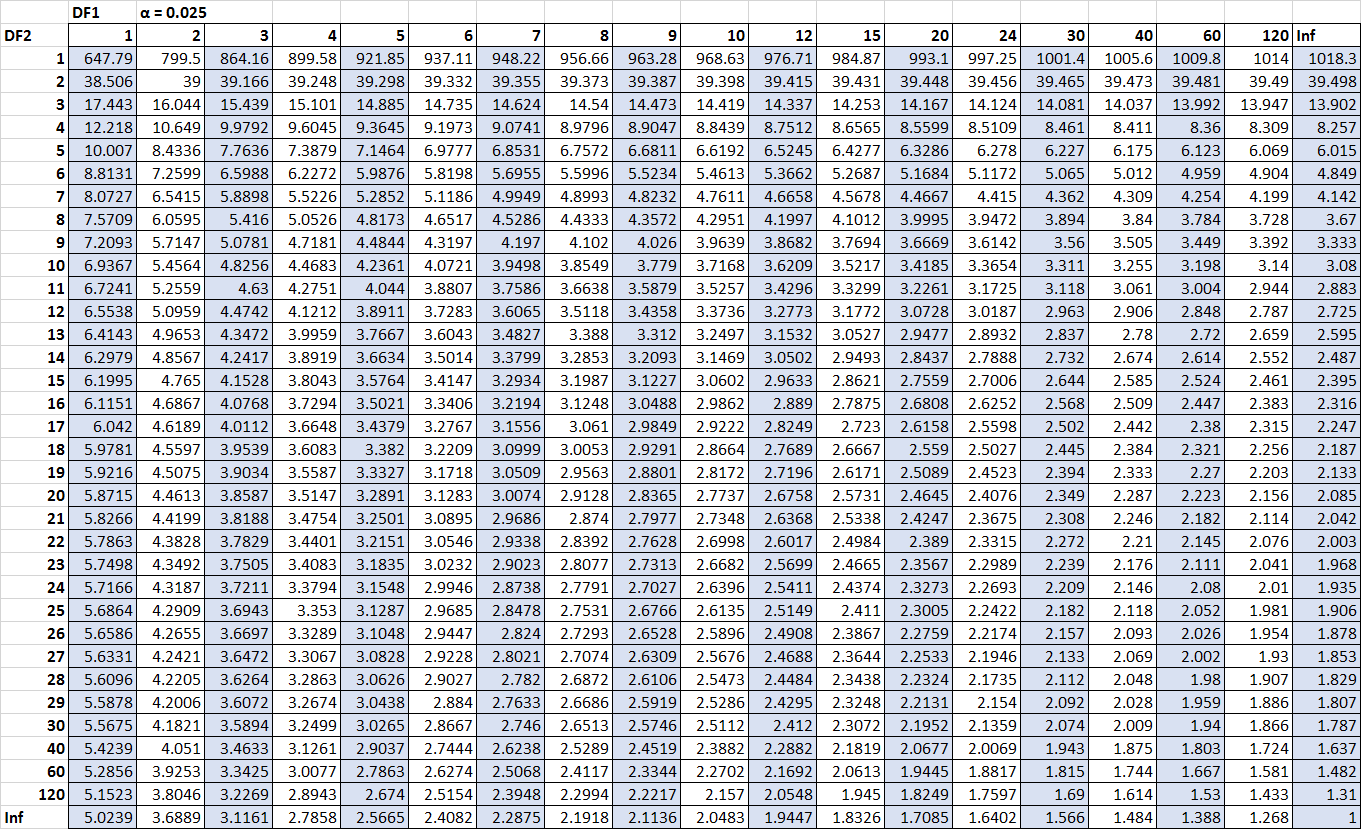
Sekarang kita dapat memasukkan semua angka ke dalam interval rumus kepercayaan:

(s ₁ ² / s ₂ ² ) * F _{n1-1, n2-1,α/2} ≤ σ ² ₁ / σ ² ₂ ≤ (s ₁ ² / s ₂ ² ) * F _{n2-1, n1-1, α/2}

(28,2 / 19,3) * (0,2839) ≤ σ ² ₁ / σ ² ₂ ≤ (28,2 / 19,3) * (3,0602)

0,4148 ≤ σ ² ₁ / σ ² ₂ ≤ 4,4714

Jadi, selang kepercayaan 95% untuk rasio varians populasi adalah (0,4148, 4,4714) .

Membuat Interval Keyakinan Menggunakan Excel

Gambar berikut memperlihatkan cara menghitung interval kepercayaan 95% untuk rasio varians populasi di Excel. Batas bawah dan atas selang kepercayaan ditunjukkan pada kolom E dan rumus yang digunakan untuk mencari batas bawah dan atas ditunjukkan pada kolom F:

Jadi, selang kepercayaan 95% untuk rasio varians populasi adalah (0,4148, 4,4714) . Ini cocok dengan apa yang kami dapatkan saat kami menghitung interval kepercayaan secara manual.

Membuat Interval Keyakinan Menggunakan R

Kode berikut mengilustrasikan cara menghitung interval kepercayaan 95% untuk rasio varians populasi di R:

 #define significance level, sample sizes, and sample variances
alpha <- .05
n1 <- 16
n2 <- 11
var1 <- 28.2
var2 <- 19.3

#define F critical values
upper_crit <- 1/qf(alpha/2, n1-1, n2-1)
lower_crit <- qf(alpha/2, n2-1, n1-1)

#find confidence interval
lower_bound <- (var1/var2) * lower_crit
upper_bound <- (var1/var2) * upper_crit

#output confidence interval
paste0("(", lower_bound, ", ", upper_bound, " )")

#[1] "(0.414899337980266, 4.47137571035219 )"

Jadi, selang kepercayaan 95% untuk rasio varians populasi adalah (0,4148, 4,4714) . Ini cocok dengan apa yang kami dapatkan saat kami menghitung interval kepercayaan secara manual.

Sumber daya tambahan

Cara membaca papan distribusi F
Cara mencari nilai kritis F di excel