Ukuran efek: apa itu dan mengapa itu penting
“Signifikansi statistik adalah hal yang paling tidak menarik dari hasil ini. Anda perlu menggambarkan hasil dalam bentuk ukuran besarnya – tidak hanya dampak suatu pengobatan terhadap masyarakat, namun juga seberapa besar dampaknya terhadap mereka. -Gene V. Kaca
Dalam statistik, kita sering menggunakan nilai p untuk menentukan apakah terdapat perbedaan yang signifikan secara statistik antara dua kelompok.
Misalnya, kita ingin mengetahui apakah dua teknik belajar yang berbeda menghasilkan nilai ujian yang berbeda. Jadi, kita mempunyai kelompok yang terdiri dari 20 siswa yang menggunakan satu teknik belajar untuk mempersiapkan ujian sementara kelompok lain yang terdiri dari 20 siswa menggunakan teknik belajar yang berbeda. Kami kemudian memberikan tes yang sama kepada setiap siswa.
Setelah menjalankan uji-t dua sampel untuk menentukan perbedaan rata-rata, kami menemukan bahwa nilai p untuk pengujian tersebut adalah 0,001. Jika kita menggunakan tingkat signifikansi 0,05, ini berarti terdapat perbedaan yang signifikan secara statistik antara hasil rata-rata kedua kelompok. Jadi, teknik belajar berdampak pada hasil tes.
Namun, meskipun nilai p memberi tahu kita bahwa teknik belajar berdampak pada nilai ujian, nilai p tidak memberi tahu kita besarnya dampak tersebut. Untuk memahami hal ini, kita perlu mengetahui ukuran efeknya .
Berapa ukuran efeknya?
Ukuran efek adalah cara untuk mengukur perbedaan antara dua kelompok.
Meskipun nilai p dapat memberi tahu kita apakah ada perbedaan yang signifikan secara statistik antara dua kelompok, ukuran efek dapat memberi tahu kita seberapa besar perbedaan tersebut. Dalam praktiknya, ukuran efek jauh lebih menarik dan berguna untuk diketahui dibandingkan nilai p.
Ada tiga cara untuk mengukur ukuran efek, bergantung pada jenis analisis yang Anda lakukan:
1. Perbedaan rata-rata yang terstandarisasi
Bila Anda ingin mempelajari perbedaan rata-rata antara dua kelompok, cara yang tepat untuk menghitung besaran pengaruh adalah dengan menggunakan perbedaan rata-rata terstandarisasi . Rumus yang paling populer untuk digunakan dikenal sebagai Cohen’s d , yang dihitung sebagai berikut:
Cohen D = ( x1 – x2 )/ s
dimana x 1 dan x 2 masing-masing adalah rata-rata sampel dari kelompok 1 dan kelompok 2, dan s adalah simpangan baku populasi dari mana kedua kelompok tersebut diambil.
Dengan menggunakan rumus ini, ukuran efek mudah diinterpretasikan:
- A d dari 1 menunjukkan bahwa rata-rata kedua kelompok berbeda satu standar deviasi.
- A d dari 2 berarti rata-rata kelompok berbeda dua standar deviasi.
- A d sebesar 2,5 menunjukkan bahwa kedua mean tersebut berbeda sebesar 2,5 standar deviasi, dan seterusnya.
Cara lain untuk menafsirkan ukuran efek adalah: ukuran efek 0,3 berarti bahwa skor rata-rata orang di Grup 2 adalah 0,3 standar deviasi di atas rata-rata orang di kelompok 1 dan oleh karena itu melebihi skor 62% dari kelompok 1 . .
Tabel berikut menunjukkan ukuran efek yang berbeda dan persentilnya yang sesuai:
| Ukuran efek | Persentase kelompok 2 yang berada di bawah rata-rata penduduk kelompok 1 |
|---|---|
| 0,0 | 50% |
| 0,2 | 58% |
| 0,4 | 66% |
| 0,6 | 73% |
| 0,8 | 79% |
| 1.0 | 84% |
| 1.2 | 88% |
| 1.4 | 92% |
| 1.6 | 95% |
| 1.8 | 96% |
| 2.0 | 98% |
| 2.5 | 99% |
| 3.0 | 99,9% |
Semakin besar effect size maka semakin besar pula perbedaan rata-rata individu pada masing-masing kelompok.
Secara umum, d sebesar 0,2 atau kurang dianggap sebagai ukuran efek kecil, d sekitar 0,5 dianggap sebagai ukuran efek sedang, dan d sebesar 0,8 atau lebih besar dianggap sebagai ukuran efek besar.
Jadi, jika rata-rata dua kelompok tidak berbeda paling sedikit 0,2 standar deviasi, maka perbedaannya tidak signifikan, bahkan jika nilai p signifikan secara statistik.
2. Koefisien korelasi
Saat Anda ingin mempelajari hubungan kuantitatif antara dua variabel, cara paling umum untuk menghitung besaran pengaruh adalah dengan menggunakan koefisien korelasi Pearson . Ini adalah ukuran hubungan linier antara dua variabel X dan Y. Nilainya antara -1 dan 1 dimana:
- -1 menunjukkan korelasi linier negatif sempurna antara dua variabel
- 0 menunjukkan tidak ada korelasi linier antara dua variabel
- Angka 1 menunjukkan korelasi linier positif sempurna antara dua variabel
Rumus untuk menghitung koefisien korelasi Pearson cukup rumit, namun dapat ditemukan di sini bagi yang berminat.
Semakin jauh koefisien korelasi dari nol, maka semakin kuat hubungan linear antara dua variabel. Hal ini juga dapat dilihat dengan membuat scatterplot sederhana dari nilai variabel X dan Y.
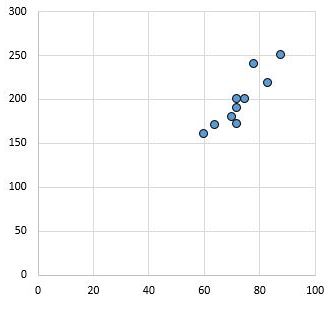
Misalnya diagram sebar berikut menunjukkan nilai dua variabel dengan koefisien korelasi r = 0,94.
Nilai tersebut jauh dari nol, menunjukkan adanya hubungan positif yang kuat antara kedua variabel.
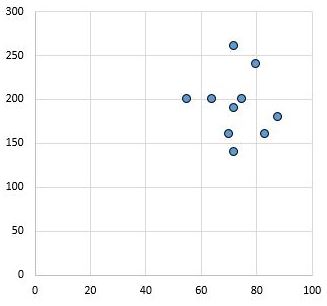
Sebaliknya, scatterplot berikut menunjukkan nilai dua variabel yang memiliki koefisien korelasi r = 0,03. Nilai ini mendekati nol, menunjukkan bahwa hampir tidak ada hubungan antara kedua variabel.
Secara umum, ukuran efek dianggap kecil jika nilai koefisien korelasi Pearson r sekitar 0,1, sedang jika r sekitar 0,3, dan besar jika r sama dengan atau lebih besar dari 0,5.
3. Rasio peluang
Saat Anda ingin mempelajari peluang keberhasilan dalam kelompok perlakuan versus peluang keberhasilan dalam kelompok kontrol, cara paling umum untuk menghitung besarnya efek adalah dengan menggunakan rasio odds .
Misalnya, kita mempunyai tabel berikut:
| Ukuran efek | #Kesuksesan | #Catur |
|---|---|---|
| Kelompok pengobatan | MEMILIKI | B |
| Kelompok kontrol | VS | D |
Rasio odds akan dihitung sebagai berikut:
Rasio peluang = (AD) / (BC)
Semakin jauh rasio odds dari 1, semakin tinggi kemungkinan pengobatan akan menghasilkan efek nyata.
Manfaat Menggunakan Ukuran Efek Dibandingkan Nilai-P
Ukuran efek memiliki beberapa keunggulan dibandingkan nilai p:
1. Ukuran efek membantu kita mendapatkan gambaran yang lebih baik tentang seberapa besar perbedaan antara dua kelompok atau seberapa kuat hubungan antara dua kelompok. Nilai p hanya dapat memberi tahu kita apakah terdapat perbedaan signifikan atau hubungan signifikan.
2. Berbeda dengan nilai p, ukuran efek dapat digunakan untuk membandingkan secara kuantitatif hasil penelitian berbeda yang dilakukan di lingkungan berbeda. Karena alasan ini, ukuran efek sering digunakan dalam meta-analisis.
3. Nilai P dapat dipengaruhi oleh ukuran sampel yang besar. Semakin besar ukuran sampel, semakin besar kekuatan statistik dari uji hipotesis, sehingga memungkinkan untuk mendeteksi efek yang kecil sekalipun. Hal ini dapat menyebabkan nilai p yang rendah, meskipun ukuran efeknya kecil dan mungkin tidak memiliki signifikansi praktis.
Sebuah contoh sederhana dapat menggambarkan hal ini dengan jelas: misalkan kita ingin mengetahui apakah dua teknik belajar menghasilkan nilai ujian yang berbeda. Kami memiliki kelompok yang terdiri dari 20 siswa yang menggunakan satu teknik belajar sementara kelompok lain yang terdiri dari 20 siswa menggunakan teknik belajar yang berbeda. Kami kemudian memberikan tes yang sama kepada setiap siswa.
Rata-rata skor kelompok 1 sebesar 90,65 dan rata-rata skor kelompok 2 sebesar 90,75 . Standar deviasi untuk sampel 1 adalah 2,77 dan standar deviasi untuk sampel 2 adalah 2,78 .
Ketika kita melakukan uji-t dua sampel independen, ternyata statistik pengujiannya adalah -0,113 dan nilai p yang sesuai adalah 0,91 . Perbedaan antara nilai rata-rata tes tidak signifikan secara statistik.
Namun, pertimbangkan jika ukuran sampel kedua sampel sama-sama 200 , namun rata-rata dan deviasi standarnya tetap sama.
Dalam kasus ini, uji t dua sampel independen akan menunjukkan bahwa statistik uji adalah -1,97 dan nilai p yang sesuai sedikit di bawah 0,05 . Perbedaan antara nilai tes rata-rata signifikan secara statistik.
Alasan mendasar mengapa ukuran sampel yang besar dapat menghasilkan kesimpulan yang signifikan secara statistik adalah karena rumus yang digunakan untuk menghitung statistik uji -t :
statistik uji t = [ ( x 1 – x 2 ) – d ] / (√ s 2 1 / n 1 + s 2 2 / n 2 )
Perhatikan bahwa jika n 1 dan n 2 kecil, penyebut bilangan bulat dari statistik uji-t adalah kecil. Dan jika dibagi dengan angka kecil, maka akan didapat angka yang besar. Artinya, statistik uji -t akan besar dan nilai p yang terkait akan kecil, sehingga menghasilkan hasil yang signifikan secara statistik.
Apa yang dianggap sebagai ukuran efek yang baik?
Pertanyaan yang sering diajukan siswa adalah: Apa yang dianggap sebagai ukuran efek yang baik?
Jawaban singkatnya: ukuran dampak tidak bisa “baik” atau “buruk” karena ukuran dampak hanya mengukur besarnya perbedaan antara dua kelompok atau kekuatan hubungan antara dua kelompok.
Namun, kita dapat menggunakan aturan praktis berikut untuk mengukur apakah besaran suatu dampak kecil, sedang, atau besar:
D Cohen:
- D sebesar 0,2 atau kurang dianggap sebagai ukuran efek yang kecil.
- A d sebesar 0,5 dianggap sebagai ukuran efek sedang.
- A d sebesar 0,8 atau lebih besar dianggap sebagai ukuran efek yang besar.
Koefisien Korelasi Pearson
- Nilai absolut r sekitar 0,1 dianggap sebagai ukuran efek yang kecil.
- Nilai absolut r sekitar 0,3 dianggap sebagai ukuran efek sedang.
- Nilai absolut r yang lebih besar dari 0,5 dianggap sebagai ukuran efek yang besar.
Namun, definisi korelasi “kuat” dapat bervariasi dari satu bidang ke bidang lainnya. Lihat artikel ini untuk lebih memahami apa yang dianggap sebagai korelasi kuat di berbagai industri.