Cara membaca tabel distribusi chi kuadrat
Tutorial ini menjelaskan cara membaca dan menginterpretasikan grafik distribusi Chi-kuadrat.
Apa tabel distribusi chi kuadrat?
Tabel distribusi Chi-kuadrat merupakan tabel yang menunjukkan nilai-nilai kritis dari distribusi Chi-kuadrat. Untuk menggunakan tabel distribusi Chi-kuadrat, Anda hanya perlu mengetahui dua nilai:
- Derajat kebebasan untuk uji Chi kuadrat
- Tingkat alfa tes (pilihan umum adalah 0,01, 0,05, dan 0,10)
Gambar berikut menunjukkan 20 baris pertama tabel distribusi Chi-kuadrat, dengan derajat kebebasan di sisi kiri tabel dan tingkat alfa di bagian atas tabel:
Catatan: Anda dapat menemukan tabel distribusi Chi-kuadrat lengkap dengan derajat kebebasan lebih banyak di sini.
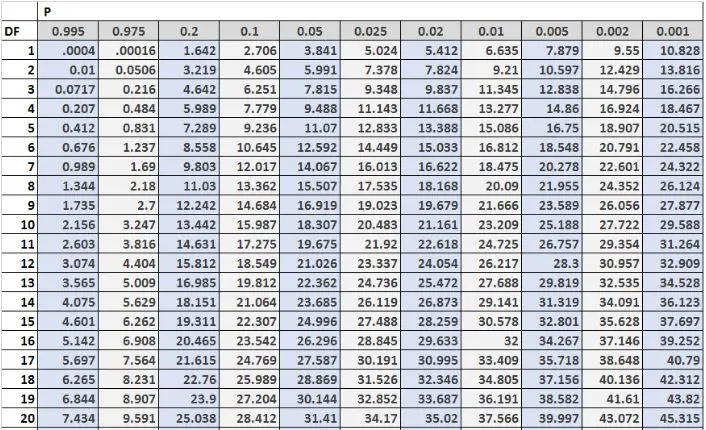
Nilai kritis dalam tabel sering dibandingkan dengan statistik uji uji Chi-kuadrat. Jika statistik uji lebih besar dari nilai kritis yang terdapat pada tabel, maka Anda dapat menolak hipotesis nol uji Chi-kuadrat dan menyimpulkan bahwa hasil pengujian tersebut signifikan secara statistik.
Contoh penggunaan tabel distribusi chi-kuadrat
Kami akan menunjukkan cara menggunakan tabel distribusi Chi-kuadrat dengan tiga jenis uji Chi-kuadrat berikut:
- Uji chi-kuadrat untuk kemandirian
- Uji chi-kuadrat untuk mengetahui kesesuaian
- Uji chi-kuadrat untuk homogenitas
Uji chi-kuadrat untuk kemandirian
Kami menggunakan uji Chi-square untuk independensi ketika kami ingin menguji apakah terdapat hubungan yang signifikan antara dua variabel kategori.
Contoh: Misalkan kita ingin mengetahui apakah gender dikaitkan dengan preferensi terhadap suatu partai politik atau tidak. Kami mengambil sampel acak sederhana dari 500 pemilih dan menanyakan preferensi partai politik mereka. Dengan menggunakan tingkat signifikansi 0,05, kami melakukan uji chi-square untuk menentukan apakah gender dikaitkan dengan preferensi partai politik. Berikut tabel hasil surveinya:
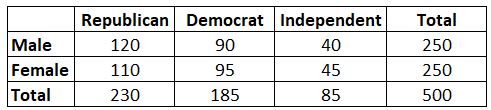
Ternyata statistik uji uji Chi-square ini adalah 0,864.
Kemudian nilai uji kritisnya dapat kita cari pada tabel distribusi Chi square. Derajat kebebasannya sama dengan (#baris-1) * (#kolom-1) = (2-1) * (3-1) = 2 dan soal memberi tahu kita bahwa kita harus menggunakan tingkat alfa 0,05 Jadi, berdasarkan tabel distribusi Chi-square, nilai kritis pengujian sebesar 5,991 .

Karena statistik pengujian kami kurang dari nilai kritis kami, kami gagal menolak hipotesis nol. Artinya, kami tidak memiliki cukup bukti untuk menyatakan adanya hubungan antara gender dan preferensi partai politik.
Uji chi-kuadrat untuk mengetahui kesesuaian
Kami menggunakan uji kesesuaian chi-kuadrat ketika kami ingin menguji apakah suatu variabel kategori mengikuti distribusi hipotetis atau tidak.
Contoh: Seorang pemilik toko mengatakan bahwa 30% dari seluruh pelanggan akhir pekannya datang pada hari Jumat, 50% pada hari Sabtu, dan 20% pada hari Minggu. Seorang peneliti independen mengunjungi toko pada akhir pekan secara acak dan menemukan 91 pelanggan pada hari Jumat, 104 pada hari Sabtu, dan 65 pada hari Minggu. Dengan menggunakan tingkat signifikansi 0,10, kami melakukan uji chi-kuadrat untuk memeriksa kesesuaian guna menentukan apakah data konsisten dengan klaim pemilik toko.
Dalam hal ini, statistik pengujiannya adalah 10.616.
Kemudian nilai uji kritisnya dapat kita cari pada tabel distribusi Chi square. Derajat kebebasannya sama dengan (#outcomes-1) = 3-1 = 2 dan soal memberitahu kita bahwa kita harus menggunakan tingkat alfa 0,10. Jadi berdasarkan tabel distribusi Chi-square, nilai kritis uji tersebut adalah 4,605 .
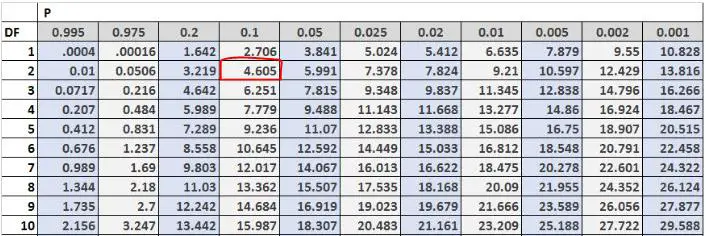
Karena statistik pengujian kami lebih besar dari nilai kritis kami, kami menolak hipotesis nol. Artinya kita mempunyai cukup bukti untuk mengatakan bahwa sebenarnya distribusi pelanggan yang datang ke toko ini pada akhir pekan tidak sama dengan 30% pada hari Jumat, 50% pada hari Sabtu, dan 20% pada hari Minggu.
Uji chi-kuadrat untuk homogenitas
Kami menggunakan uji Chi-kuadrat untuk homogenitas ketika kami ingin menguji secara formal apakah terdapat perbedaan proporsi antara beberapa kelompok.
Contoh: Sebuah pusat pelatihan bola basket ingin melihat apakah dua program pelatihan baru meningkatkan proporsi pemainnya yang lulus tes menembak yang sulit. 172 pemain secara acak ditugaskan ke program 1, 173 ke program 2, dan 215 ke program saat ini. Setelah menggunakan program latihan selama sebulan, pemain kemudian mengikuti tes menembak. Tabel di bawah ini menunjukkan jumlah pemain yang lulus tes menembak berdasarkan program yang mereka gunakan.

Dengan menggunakan tingkat signifikansi 0,05, kami melakukan uji chi-kuadrat untuk menentukan apakah tingkat keberhasilan setiap program pelatihan sama.
Ternyata statistik uji uji Chi-square ini adalah 4,208.
Kemudian nilai uji kritisnya dapat kita cari pada tabel distribusi Chi square. Derajat kebebasannya sama dengan (#baris-1) * (#kolom-1) = (2-1) * (3-1) = 2 dan soal memberi tahu kita bahwa kita harus menggunakan tingkat alfa 0,05 Jadi, berdasarkan tabel distribusi Chi-square, nilai kritis pengujian sebesar 5,991 .

Karena statistik pengujian kami kurang dari nilai kritis kami, kami gagal menolak hipotesis nol. Artinya, kami tidak memiliki cukup bukti untuk mengatakan bahwa ketiga program pelatihan tersebut memberikan hasil yang berbeda.