Socs: akronim yang berguna untuk menggambarkan distribusi
Dalam statistik, kita sering kali ingin memahami bagaimana sekumpulan data didistribusikan. Secara khusus, ada empat hal yang berguna untuk diketahui tentang distribusi:
1 . Membentuk
- Apakah distribusinya simetris atau condong ke satu sisi?
- Apakah distribusinya unimodal (satu puncak) atau bimodal (dua puncak)?
2. Pencilan
- Apakah ada outlier dalam distribusinya?
3. Pusat
- Apa mean, median dan cara distribusinya?
4. Penyebaran
- Berapakah jangkauan, jangkauan antarkuartil, simpangan baku, dan varians distribusinya?
SOCS adalah akronim berguna yang dapat kita gunakan untuk mengingat empat hal ini. Artinya “bentuk, outlier, pusat, penyebaran”.
Mari kita lihat contoh sederhana bagaimana menggunakan SOCS untuk mendeskripsikan suatu distribusi.
Contoh: Cara menggunakan SOCS untuk mendeskripsikan suatu distribusi
Katakanlah kita memiliki kumpulan data berikut yang menunjukkan tinggi sampel dari 20 tanaman berbeda.
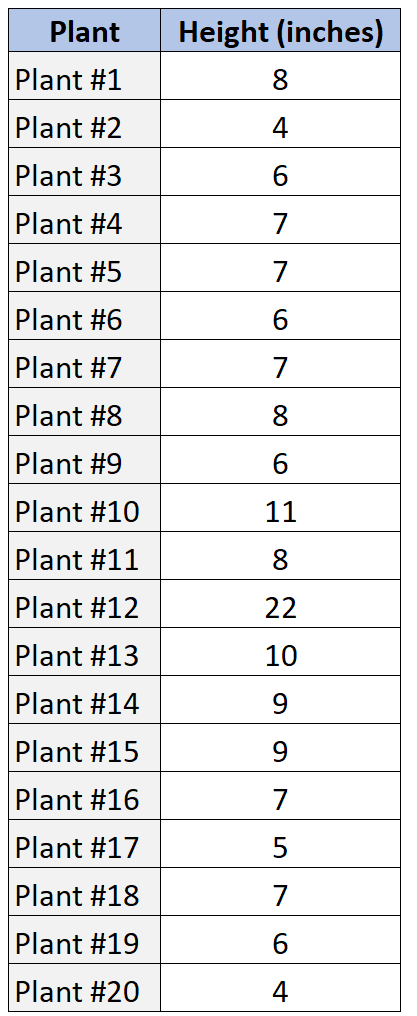
Inilah cara kita menggunakan SOCS untuk mendeskripsikan distribusi nilai data ini.
Membentuk
Pertama, kami ingin menggambarkan bentuk distribusinya.
Cara yang berguna untuk memvisualisasikan bentuk distribusi adalah dengan membuat histogram, yang menampilkan frekuensi setiap nilai dalam kumpulan data:
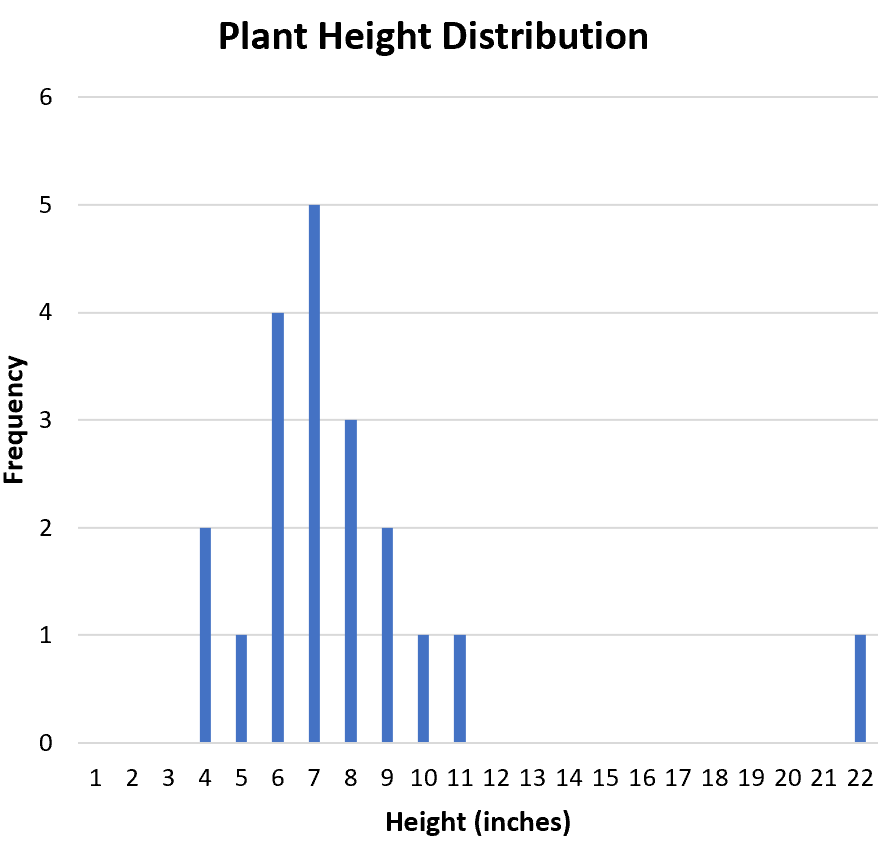
Apakah distribusinya simetris atau condong ke satu sisi? Dari histogram terlihat distribusinya kurang lebih simetris. Dengan kata lain, nilai-nilai tidak bias dalam satu atau lain cara.
Apakah distribusinya unimodal (satu puncak) atau bimodal (dua puncak)? Distribusinya unimodal. Ini memiliki puncak pada nilai “7”.
Pencilan
Selanjutnya, kami ingin menentukan apakah ada outlier dalam kumpulan data. Dari histogram kita dapat memeriksa distribusi secara visual dan melihat bahwa 22 berpotensi merupakan outlier:
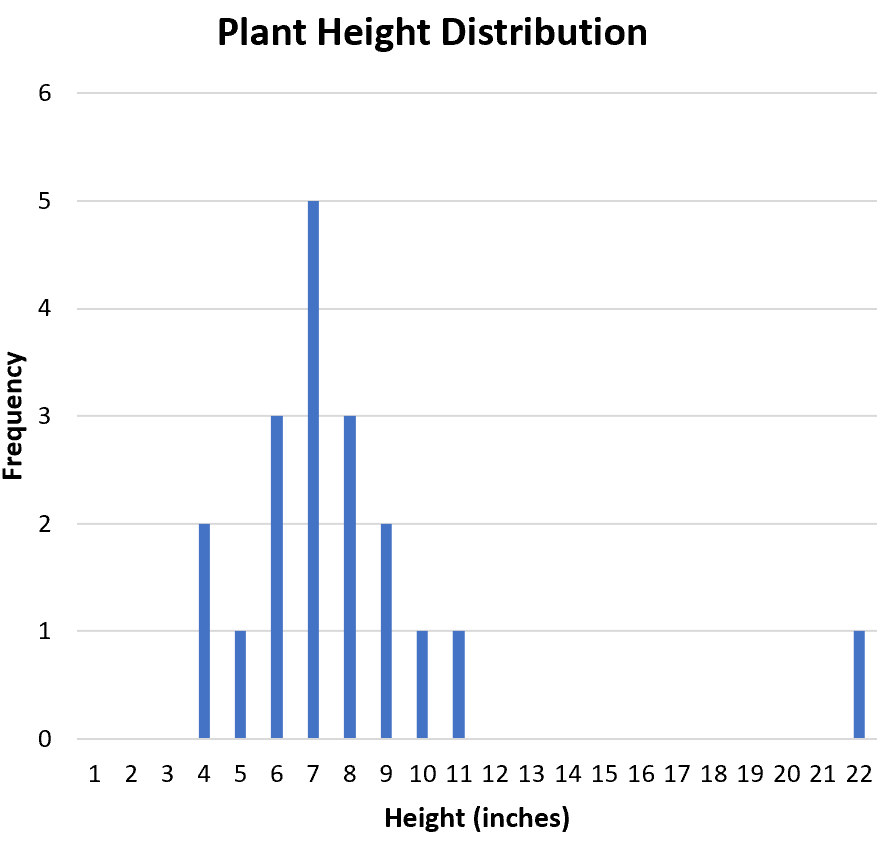
Cara umum untuk mendefinisikan outlier secara formal adalah nilai apa pun yang 1,5 kali rentang antarkuartil di atas kuartil ketiga atau di bawah kuartil pertama.
Dengan menggunakan kalkulator rentang antarkuartil, kita dapat memasukkan 20 nilai data mentah dan melihat bahwa kuartil ketiga adalah 9 , rentang antarkuartil adalah 3 , dan oleh karena itu nilai apa pun yang lebih besar dari 9 + (1,5*3) = 13,5 adalah outlier, menurut definisi.
Karena 22 lebih besar dari 13,5, kita dapat menyatakan 22 sebagai outlier.
Tengah
Kami kemudian ingin menjelaskan di mana pusat distribusi berada. Tiga ukuran tendensi sentral yang umum digunakan adalah mean, median, dan mode.
Mean : Ini adalah nilai rata-rata dari distribusi. Kami menemukannya dengan menjumlahkan semua nilai individual dan kemudian membaginya dengan jumlah total nilai:
Rata-rata = (8+4+6+7+7+6+7+8+6+11+8+22+10+9+9+7+5+7+6+4) / 20 = 7,85
Median: Ini adalah nilai “rata-rata” dari distribusi. Kami menemukannya dengan mengurutkan semua nilai dari terkecil hingga terbesar dan kemudian mengidentifikasi nilai mediannya. Ternyata menjadi 7 .
4, 4, 5, 6, 6, 6, 6, 7, 7, 7 , 7 , 7, 8 , 8, 8, 9, 9, 10, 11, 22
Mode: Ini adalah nilai yang paling sering muncul. Ternyata menjadi 7 .
Menyebar
Selanjutnya kami ingin menguraikan sebaran nilai dalam distribusi. Empat ukuran dispersi umum yang dapat kita gunakan adalah jangkauan, jangkauan antarkuaril, deviasi standar, dan varians.
Rentang: Ini adalah selisih antara nilai terbesar dan terkecil dalam kumpulan data. Ternyata 22 – 4 = 18 .
Rentang Interkuartil: Mengukur lebar 50% tengah nilai data. Memasukkan 20 nilai data mentah ke dalam kalkulator rentang interkuartil, kita dapat melihat bahwa ini sama dengan 3 .
Deviasi standar: Ini adalah ukuran distribusi rata-rata nilai data. Memasukkan 20 nilai data mentah ke dalam kalkulator varians dan deviasi standar, kita dapat melihat bahwa deviasi standarnya sama dengan 3,69 .
Varians: Ini hanyalah deviasi standar, kuadrat. Ini sama dengan 3,69 2 = 13,63 .
Kesimpulan
Dengan menggunakan SOCS sebagai panduan, kami dapat menggambarkan distribusi tinggi tanaman sebagai berikut:
- Distribusinya bersifat unimodal dan simetris, artinya hanya mempunyai satu puncak dan tidak condong ke satu sisi atau sisi lainnya.
- Distribusinya memiliki satu outlier: 22.
- Distribusi tersebut mempunyai mean 7,85, median 7, dan modus 7.
- Distribusinya mempunyai rentang 18, rentang interkuartil 3, simpangan baku 3,69, dan varian 13,63.
Perhatikan bahwa kita dapat menggunakan SOCS untuk mendeskripsikan distribusi apa pun, yang merupakan cara yang berguna bagi kita untuk memahami sepenuhnya bentuk suatu distribusi, apakah distribusi tersebut memiliki outlier, di mana kira-kira pusatnya, dan bagaimana nilai datanya didistribusikan. adalah.