Cara melakukan tes peringkat bertanda wilcoxon

Uji peringkat bertanda Wilcoxon adalah versi nonparametrik dari uji t berpasangan . Ini digunakan untuk menguji apakah ada perbedaan yang signifikan antara dua rata-rata populasi.

Kapan menggunakan tes peringkat bertanda Wilcoxon

Gunakan uji Wilcoxon Signed Rank jika Anda ingin menggunakan uji t berpasangan namun distribusi perbedaan antar pasangan sangat tidak terdistribusi normal .

Cara termudah untuk menentukan apakah perbedaan tersebut tidak terdistribusi secara normal adalah dengan membuat histogram perbedaan tersebut dan melihat apakah perbedaan tersebut mengikuti distribusi berbentuk “lonceng” yang agak normal.

Perlu diingat bahwa uji t berpasangan cukup kuat terhadap penyimpangan dari normalitas, sehingga penyimpangan dari distribusi normal harus cukup besar untuk membenarkan penggunaan uji Wilcoxon Signed Rank.

Cara Mengikuti Tes Peringkat Bertanda Wilcoxon

Contoh berikut mengilustrasikan cara melakukan tes Wilcoxon Signed Rank.

Seorang pelatih bola basket ingin mengetahui apakah program latihan tertentu meningkatkan jumlah lemparan bebas yang dilakukan oleh para pemainnya. Untuk mengujinya, ia meminta 15 pemain melakukan 20 lemparan bebas masing-masing sebelum dan sesudah program latihan.

Karena setiap pemain dapat “dipasangkan” dengan dirinya sendiri, pelatih berencana menggunakan uji-t berpasangan untuk mengetahui apakah terdapat perbedaan yang signifikan antara rata-rata jumlah lemparan bebas yang dilakukan sebelum dan sesudah program latihan. pelatihan.

Namun, distribusi perbedaannya ternyata tidak normal, itulah sebabnya pelatih menggunakan tes peringkat bertanda tangan Wilcoxon.

Tabel berikut menyajikan jumlah lemparan bebas yang dilakukan (dari 20 percobaan) oleh masing-masing 15 pemain, sebelum dan sesudah program latihan:

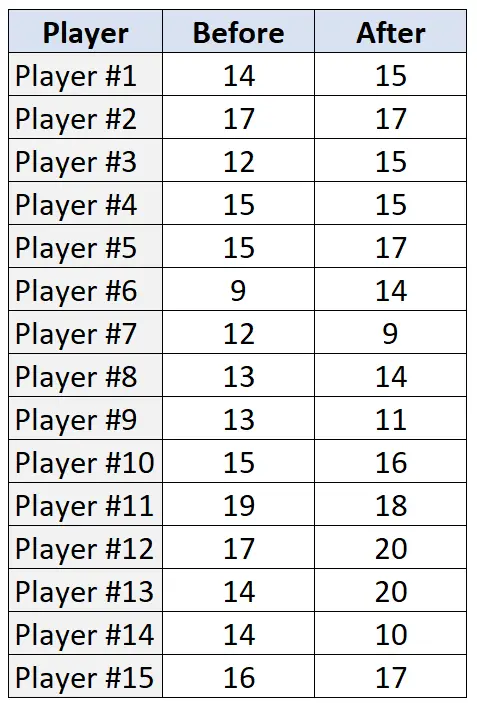
Langkah 1: Nyatakan hipotesis nol dan hipotesis alternatif.

H ₀ : Selisih median kedua kelompok adalah nol.

H _A : Selisih mediannya negatif. (misalnya pemain melakukan lebih sedikit lemparan bebas sebelum berpartisipasi dalam program latihan)

Langkah 2: Temukan selisih dan selisih mutlak untuk setiap pasangan.

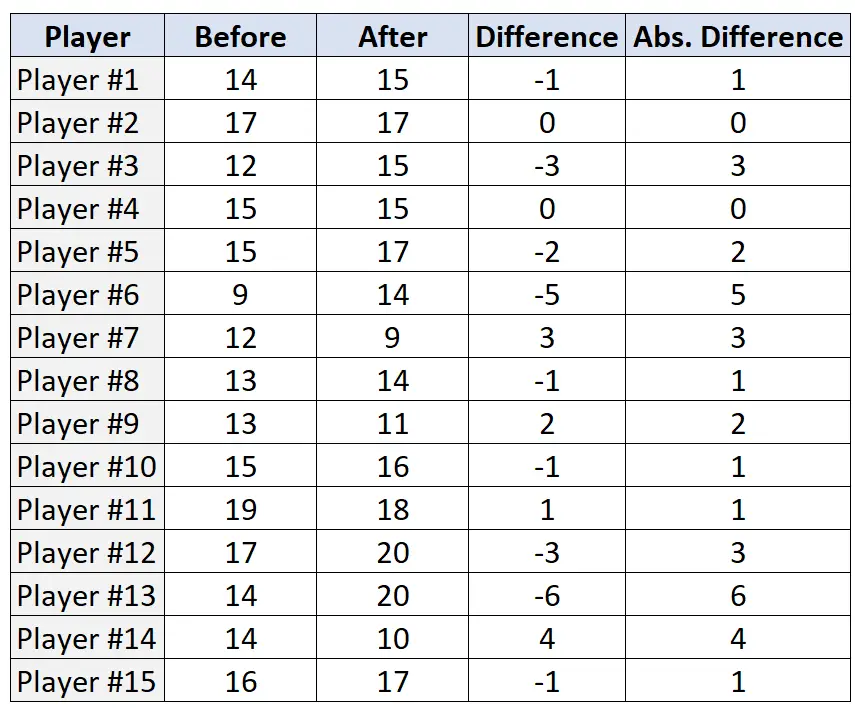
Langkah 3: Beri peringkat pasangan berdasarkan perbedaan absolut dan tetapkan peringkat dari perbedaan absolut terkecil hingga terbesar. Abaikan pasangan yang memiliki perbedaan absolut “0” dan tetapkan peringkat rata-rata jika seri.

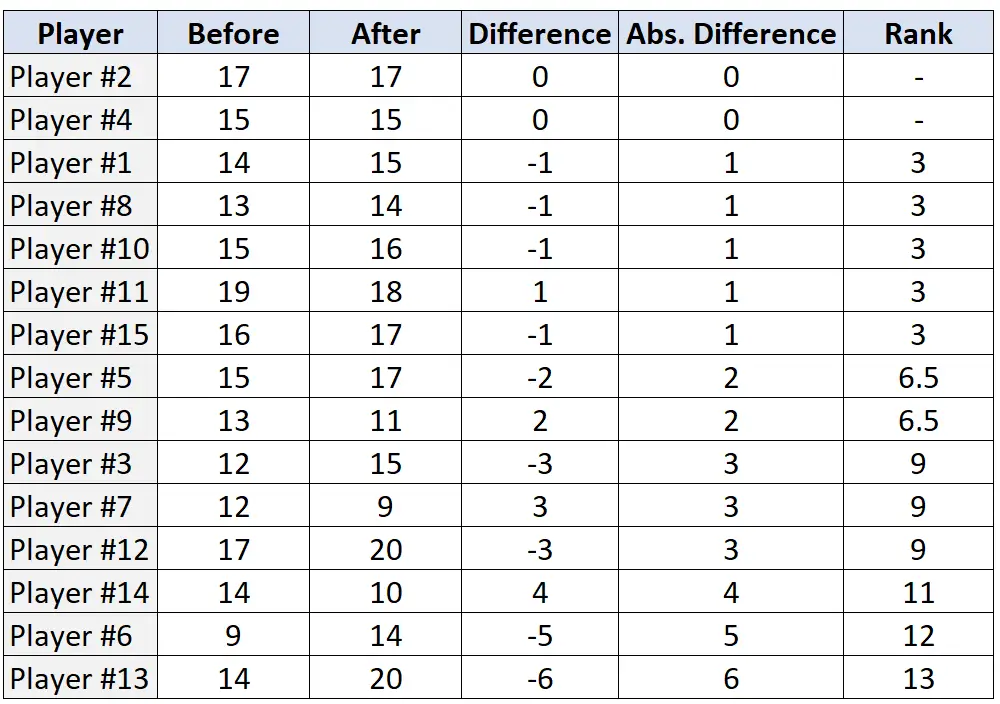
Langkah 4: Temukan jumlah peringkat positif dan peringkat negatif.

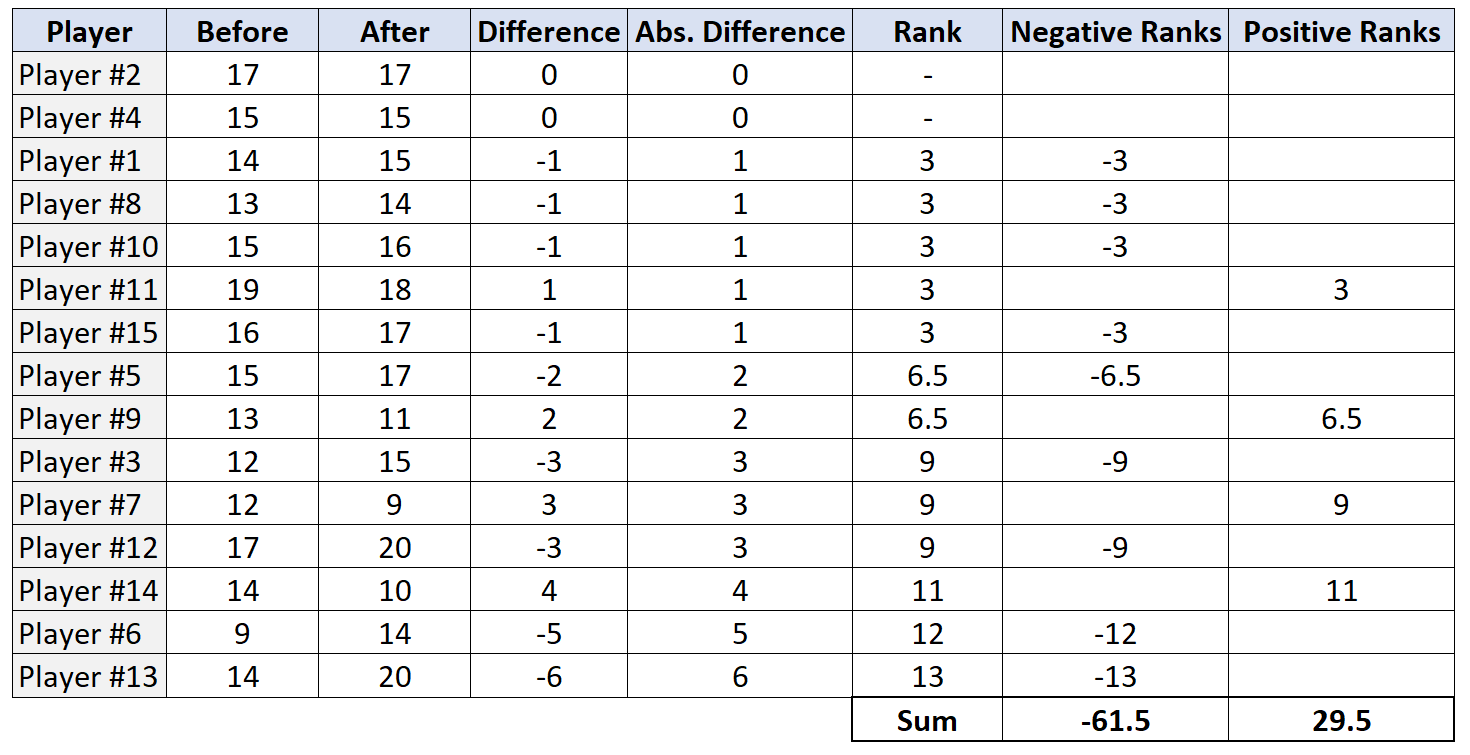
Langkah 5: Tolak atau jangan tolak hipotesis nol.

Statistik uji W adalah nilai absolut terkecil dari rangking positif dan rangking negatif. Dalam hal ini nilai terkecilnya adalah 29,5. Jadi statistik pengujian kami adalah W = 29.5 .

Untuk menentukan apakah kita harus menolak hipotesis nol atau tidak, kita dapat merujuk pada nilai kritis yang terdapat dalam tabel nilai kritis uji peringkat bertanda Wilcoxon yang sesuai dengan n dan tingkat alfa yang dipilih.

Jika statistik pengujian kita, W, kurang dari atau sama dengan nilai kritis dalam tabel, kita dapat menolak hipotesis nol. Jika tidak, kita akan gagal menolak hipotesis nol.

Nilai kritis yang sesuai dengan tingkat alfa 0,05 dan n = 13 (jumlah total pasangan dikurangi dua yang peringkatnya tidak kami hitung karena perbedaan pengamatannya sebesar 0) adalah 17 .

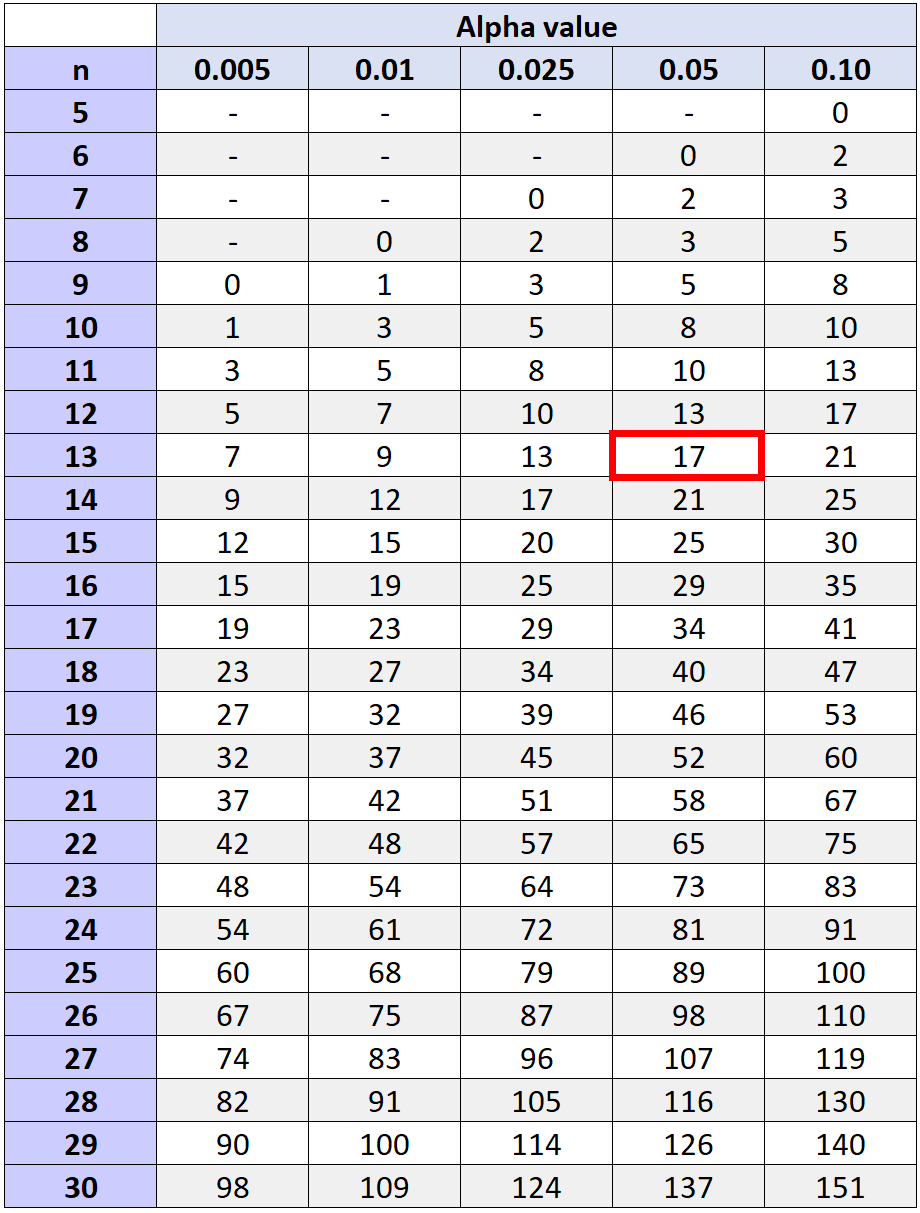
Karena statistik pengujian kami (W = 29,5) tidak kurang dari atau sama dengan 17, kami gagal menolak hipotesis nol. Kami tidak mempunyai cukup bukti untuk mengatakan bahwa program latihan menghasilkan peningkatan signifikan dalam jumlah lemparan bebas yang dilakukan pemain.

Catatan: Gunakan Kalkulator Tes Peringkat Bertanda Wilcoxon jika Anda ingin melakukan tes menggunakan kalkulator dan bukan dengan tangan.