Panduan prosedur benjamini-hochberg
Setiap kali Anda melakukan uji statistik, ada kemungkinan Anda mendapatkan nilai p kurang dari 0,05 secara kebetulan, meskipun hipotesis nol Anda benar.
Misalnya, Anda ingin mengetahui apakah tanaman tertentu memiliki tinggi rata-rata lebih dari 10 inci. Hipotesis nol dan alternatif Anda untuk pengujian adalah:
H 0 : μ = 10 inci
HA : μ > 10 inci
Untuk menguji hipotesis ini, Anda dapat keluar dan mengumpulkan sampel acak sebanyak 20 tanaman untuk diukur. Meskipun tinggi rata-rata sebenarnya dari spesies tanaman ini adalah 10 inci, ada kemungkinan Anda telah memilih sampel dari 20 tanaman yang sangat tinggi, sehingga Anda menolak hipotesis nol.
Sekalipun hipotesis nol itu benar (tinggi rata-rata tanaman ini sebenarnya 10 inci), Anda menolaknya. Dalam statistik, kami menyebutnya sebagai “penemuan palsu”. Anda mengklaim telah membuat penemuan – sebuah “hasil yang signifikan” – namun hal ini sebenarnya salah.
Sekarang bayangkan menjalankan 100 uji statistik sekaligus. Dengan menggunakan tingkat alfa 0,05, hanya ada 5% peluang untuk membuat penemuan palsu dengan pengujian individual, namun karena Anda melakukan begitu banyak pengujian, Anda hanya memperkirakan hanya sekitar 5 dari 100 yang menghasilkan penemuan palsu.
Di dunia modern, penemuan palsu dapat menjadi masalah umum karena teknologi telah memungkinkan para peneliti melakukan ratusan atau bahkan ribuan uji statistik dalam satu waktu.
Misalnya, peneliti medis dapat melakukan uji statistik terhadap puluhan ribu gen sekaligus. Bahkan dengan tingkat penemuan palsu yang hanya sebesar 5%, hal ini berarti ratusan pengujian dapat menghasilkan penemuan palsu.
Salah satu cara untuk mengendalikan tingkat penemuan palsu adalah dengan menggunakan apa yang disebut prosedur Benjamini-Hochberg.
Prosedur Benjamini-Hochberg
Prosedur Benjamini-Hochberg bekerja sebagai berikut:
Langkah 1: Lakukan semua uji statistik Anda dan temukan nilai p untuk setiap pengujian.
Langkah 2: Urutkan nilai-p dalam urutan menurun, berikan peringkat untuk masing-masing nilai: nilai terkecil memiliki peringkat 1, nilai terkecil berikutnya memiliki peringkat 2, dan seterusnya.
Langkah 3: Hitung nilai kritis Benjamini-Hochberg untuk setiap nilai p, menggunakan rumus (i/m)*Q
Emas:
i = pangkat nilai p
m = jumlah total tes
Q = tingkat penemuan palsu yang Anda pilih
Langkah 4: Temukan nilai p terbesar yang kurang dari nilai kritis. Tetapkan setiap nilai p yang kurang dari nilai p ini sebagai signifikan.
Contoh berikut mengilustrasikan bagaimana melaksanakan prosedur ini dengan nilai-nilai konkrit.
Contoh
Katakanlah peneliti ingin menentukan apakah 20 variabel berbeda berhubungan dengan penyakit jantung atau tidak. Mereka melakukan 20 uji statistik individu sekaligus dan menerima nilai p untuk setiap pengujian. Tabel berikut menunjukkan nilai p untuk setiap pengujian, diurutkan dalam urutan menurun.
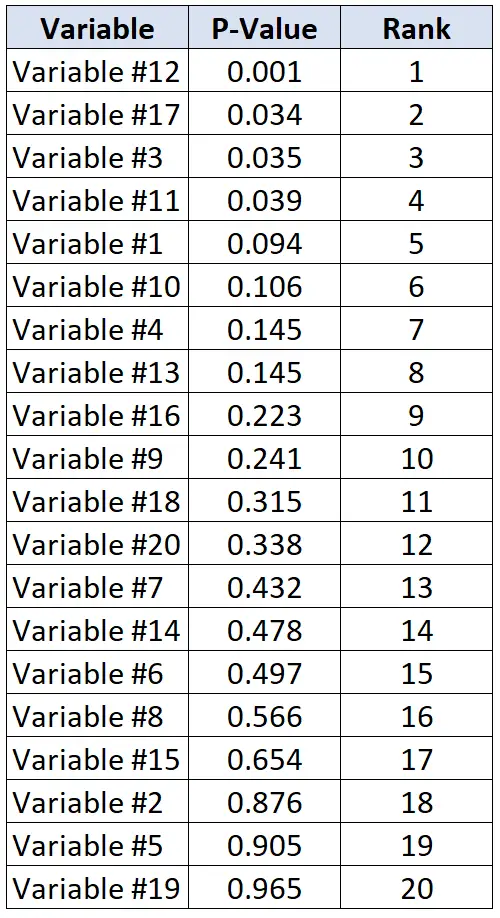
Misalkan peneliti bersedia menerima tingkat penemuan palsu sebesar 20%. Jadi, untuk menghitung nilai kritis Benjamini-Hochberg untuk setiap nilai p, kita dapat menggunakan rumus berikut: (i/20)*0,2 dimana i = pangkat dari nilai p tersebut.
Tabel berikut menunjukkan nilai kritis Benjamini-Hochberg untuk setiap nilai p individu:
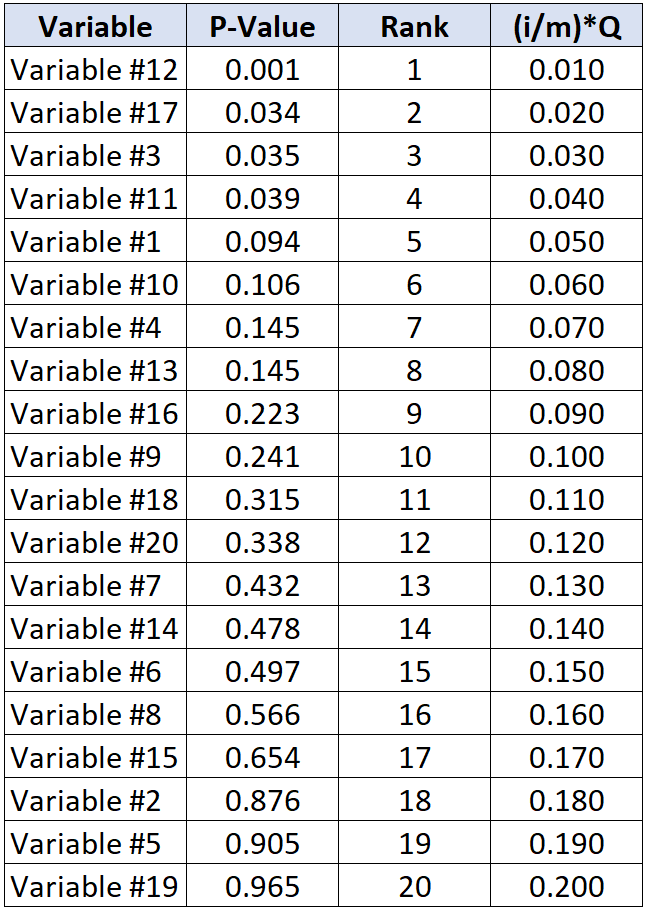
Pengujian dengan p-value terbesar di bawah nilai kritis Benjamini-Hochberg adalah variabel #11 yang mempunyai nilai p-value sebesar 0,039 dan nilai kritis BH sebesar 0,040.
Dengan demikian, pengujian ini dan semua pengujian dengan nilai p yang lebih kecil akan dianggap signifikan.
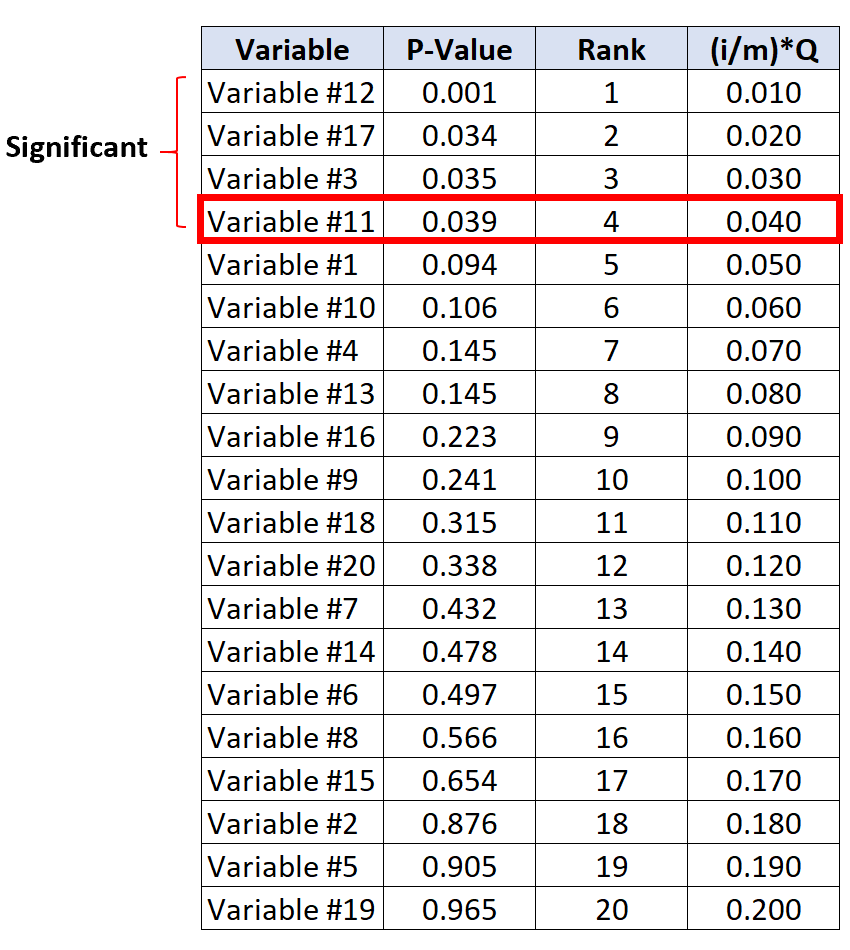
Perhatikan bahwa meskipun variabel #17 dan #3 tidak memiliki nilai p yang lebih kecil dari nilai kritis BH-nya, namun tetap dianggap signifikan karena memiliki nilai p yang lebih kecil dibandingkan variabel #11.
Bagaimana memilih tingkat penemuan palsu
Salah satu langkah terpenting dalam prosedur Benjamini-Hochberg adalah memilih tingkat penemuan palsu. Anda harus memilih tingkat penemuan palsu Anda sebelum mengumpulkan data atau melakukan uji statistik.
Biasanya, Anda akan melakukan sejumlah besar uji statistik selama fase eksplorasi analisis Anda, yang kemudian akan Anda tindak lanjuti dengan pengujian lain untuk mengeksplorasi hasil Anda lebih lanjut.
Jika pengujian lanjutan tidak mahal, maka Anda dapat mempertimbangkan untuk menetapkan tingkat penemuan palsu yang lebih tinggi, karena meskipun Anda memiliki beberapa penemuan palsu, kemungkinan besar Anda akan menemukan penemuan palsu tersebut pada pengujian berikutnya.
Selain itu, jika kerugian akibat kehilangan penemuan penting cukup tinggi, Anda mungkin ingin meningkatkan tingkat penemuan palsu agar tidak melewatkan hal penting.
Bergantung pada biaya penelitian Anda dan pentingnya tidak melewatkan temuan penting apa pun, tingkat penemuan palsu akan bervariasi dari satu situasi ke situasi lainnya.
Sumber daya tambahan
Penjelasan tentang nilai P dan signifikansi statistik
Berapa tingkat kesalahan per keluarga?