Penjelasan sederhana tentang koreksi kontinuitas dalam statistik
Koreksi kontinuitas diterapkan ketika Anda ingin menggunakan distribusi kontinu untuk memperkirakan distribusi diskrit. Umumnya digunakan ketika Anda ingin menggunakan distribusi normal untuk memperkirakan distribusi binomial .
Ingatlah bahwa distribusi binomial memberi tahu kita probabilitas keberhasilan x dalam n percobaan, mengingat probabilitas keberhasilan dalam satu percobaan adalah p . Untuk menjawab pertanyaan tentang probabilitas dengan distribusi binomial, kita cukup menggunakan kalkulator distribusi binomial , tetapi kita juga dapat memperkirakan probabilitas menggunakan distribusi normal dengan koreksi kontinuitas.
Koreksi kontinuitas adalah nama yang diberikan untuk menambah atau mengurangi 0,5 dari nilai x diskrit .
Misalnya, kita ingin mencari peluang sebuah koin mendarat di kepala yang kurang dari atau sama dengan 45 kali dalam 100 kali pelemparan. Artinya, kita ingin mencari P(X ≤ 45). Untuk menggunakan distribusi normal untuk memperkirakan distribusi binomial, kita perlu mencari P(X ≤ 45,5).
Tabel berikut menunjukkan kapan Anda harus menambah atau mengurangi 0,5, bergantung pada jenis probabilitas yang ingin Anda temukan:
| Gunakan distribusi binomial | Menggunakan distribusi normal dengan koreksi kontinuitas |
|---|---|
| X = 45 | 44,5 < X < 45,5 |
| X ≤ 45 | X < 45,5 |
| X < 45 | X < 44,5 |
| X ≥ 45 | X > 44,5 |
| X > 45 | X > 45,5 |
Catatan:
Koreksi kontinuitas hanya dapat diterapkan pada distribusi normal untuk mendekati distribusi binomial jika n*p dan n*(1-p) keduanya minimal 5.
Misalnya n = 15 dan p = 0,6. Pada kasus ini:
n*p = 15 * 0,6 = 9
n*(1-p) = 15 * (1 – 0,6) = 15 * (0,4) = 6
Karena kedua angka ini lebih besar atau sama dengan 5, maka penerapan koreksi kontinuitas dapat diterima dalam skenario ini.
Contoh berikut mengilustrasikan bagaimana menerapkan koreksi kontinuitas pada distribusi normal untuk mendekati distribusi binomial.
Contoh penerapan koreksi kontinuitas
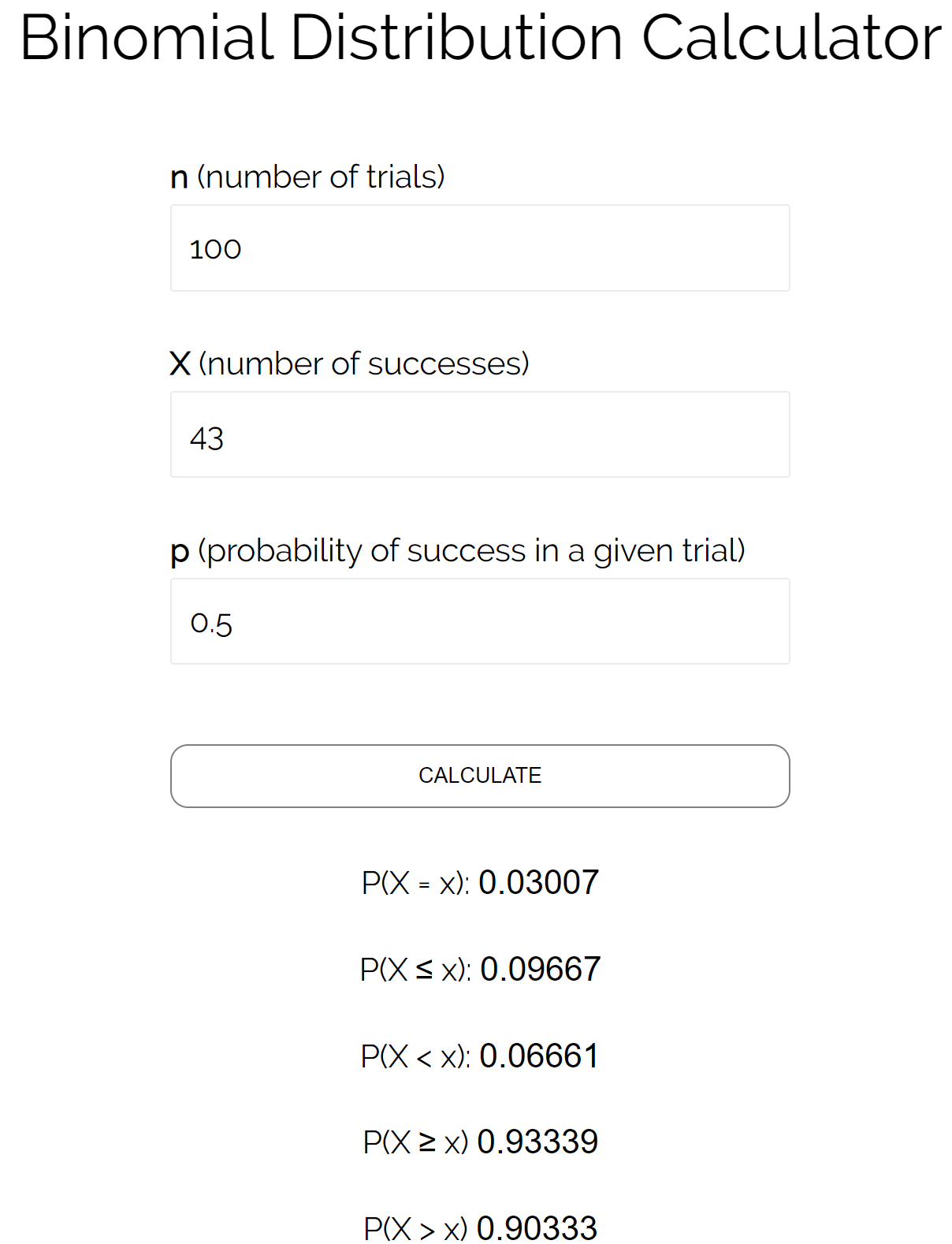
Misalkan kita ingin mengetahui probabilitas sebuah koin mendarat di kepala kurang dari atau sama dengan 43 kali dalam 100 kali pelemparan. Pada kasus ini:
n = jumlah percobaan = 100
X = jumlah keberhasilan = 43
p = probabilitas keberhasilan dalam suatu percobaan = 0,50
Kita dapat memasukkan angka-angka ini ke dalam kalkulator distribusi binomial untuk melihat bahwa probabilitas koin mendarat di kepala yang kurang dari atau sama dengan 43 kali adalah 0,09667 .
Untuk memperkirakan distribusi binomial dengan menerapkan koreksi kontinuitas pada distribusi normal, kita dapat menggunakan langkah-langkah berikut:
Langkah 1: Verifikasi bahwa n*p dan n*(1-p) keduanya setidaknya 5 .
n*p = 100*0,5 = 50
n*(1-p) = 100*(1 – 0,5) = 100*0,5 = 50
Kedua angka tersebut lebih besar atau sama dengan 5, jadi kita bisa melanjutkan.
Langkah 2: Tentukan apakah akan menambah atau mengurangi 0,5
Mengacu pada tabel di atas, kita melihat bahwa kita seharusnya menambahkan 0,5 ketika kita bekerja dengan probabilitas dalam bentuk X ≤ 43. Jadi, kita akan menemukan P(X< 43.5).
Langkah 3: Temukan mean (μ) dan deviasi standar (σ) dari distribusi binomial.
μ = n*p = 100*0,5 = 50
σ = √ n*p*(1-p) = √ 100*.5*(1-.5) = √ 25 = 5
Langkah 4: Temukan skor-z menggunakan mean dan deviasi standar yang ditemukan pada langkah sebelumnya.
z = (x – μ) / σ = (43,5 – 50) / 5 = -6,5 / 5 = -1,3.
Langkah 5: Gunakan tabel Z untuk mencari probabilitas yang terkait dengan skor z.
Berdasarkan Tabel Z, probabilitas yang terkait dengan z = -1.3 adalah 0.0968 .
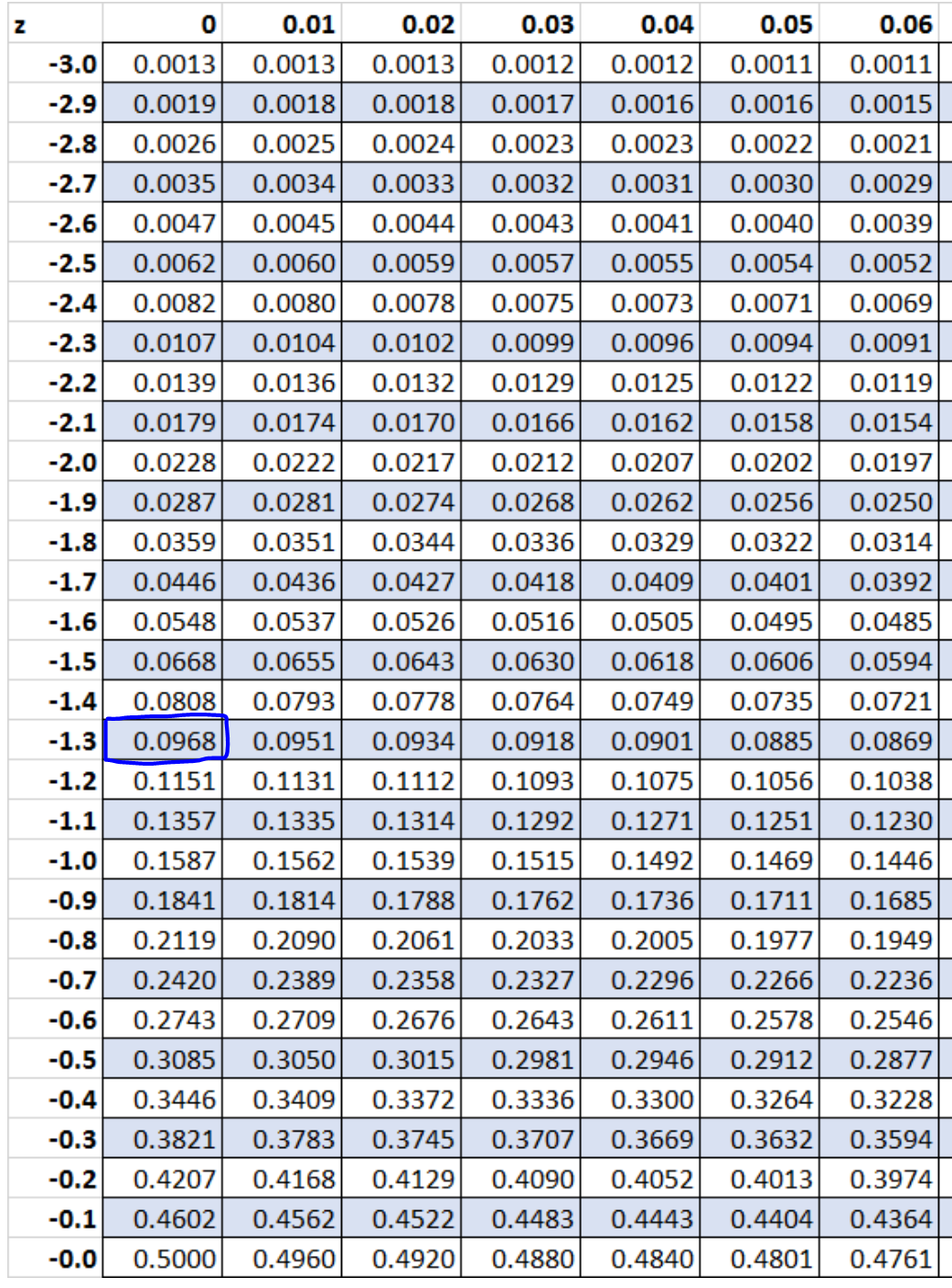
Jadi probabilitas pasti yang kita temukan dengan menggunakan distribusi binomial adalah 0,09667 sedangkan probabilitas perkiraan yang kita temukan menggunakan koreksi kontinuitas dengan distribusi normal adalah 0,0968 . Kedua nilai ini cukup tertutup.
Kapan menggunakan koreksi kontinuitas
Sebelum perangkat lunak statistik modern ada dan perhitungan harus dilakukan secara manual, koreksi kontinuitas sering digunakan untuk mencari probabilitas yang melibatkan distribusi diskrit. Saat ini, koreksi kontinuitas kurang berperan dalam menghitung probabilitas karena kita biasanya dapat mengandalkan perangkat lunak atau kalkulator untuk menghitung probabilitas.
Sebaliknya, ini hanyalah topik yang dibahas dalam kursus statistik untuk menggambarkan hubungan antara distribusi binomial dan distribusi normal dan untuk menunjukkan bahwa distribusi normal dapat mendekati distribusi binomial dengan menerapkan koreksi kontinuitas.
Kalkulator koreksi kontinuitas
Gunakan kalkulator koreksi kontinuitas untuk secara otomatis menerapkan koreksi kontinuitas pada distribusi normal untuk memperkirakan probabilitas binomial.