Cara melakukan regresi kuadrat di stata

Jika dua variabel memiliki hubungan linier, Anda sering kali dapat menggunakan regresi linier sederhana untuk mengukur hubungannya.

Namun, jika dua variabel memiliki hubungan kuadrat, Anda dapat menggunakan regresi kuadrat untuk mengukur hubungannya.

Tutorial ini menjelaskan cara melakukan regresi kuadratik di Stata.

Contoh: regresi kuadratik di Stata

Misalkan kita ingin memahami hubungan antara jumlah jam kerja dan kebahagiaan. Kami memiliki data berikut mengenai jumlah jam kerja per minggu dan tingkat kebahagiaan yang dilaporkan (dalam skala 0 hingga 100) untuk 16 orang berbeda:

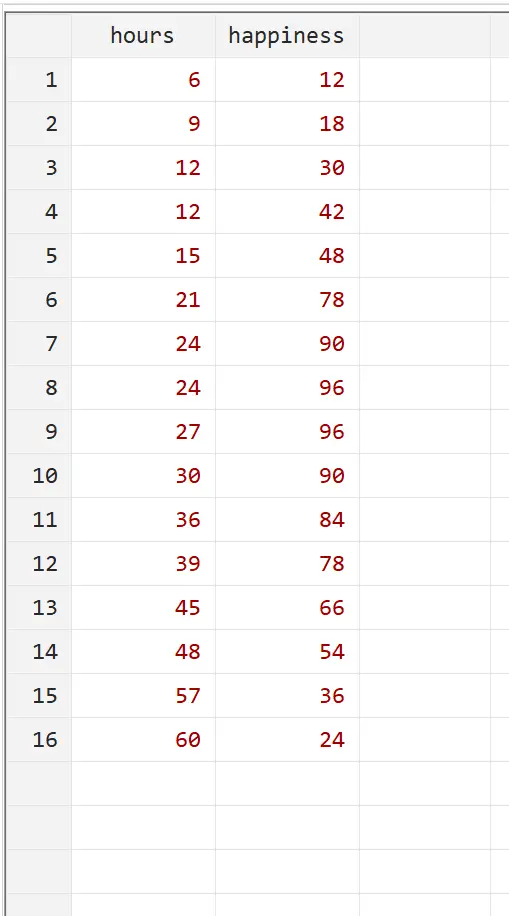
Anda dapat mereproduksi contoh ini dengan memasukkan data persis ini ke dalam Stata menggunakan Data > Editor Data > Editor Data (Edit) di menu atas.

Gunakan langkah-langkah berikut untuk melakukan regresi kuadratik di Stata.

Langkah 1: Visualisasikan datanya.

Sebelum kita dapat menggunakan regresi kuadrat, kita harus memastikan bahwa hubungan antara variabel penjelas (jam) dan variabel respon (kebahagiaan) memang bersifat kuadrat. Jadi mari kita visualisasikan data menggunakan scatterplot dengan mengetikkan perintah berikut di kotak Command:

membubarkan jam-jam kebahagiaan

Ini menghasilkan plot sebar berikut:

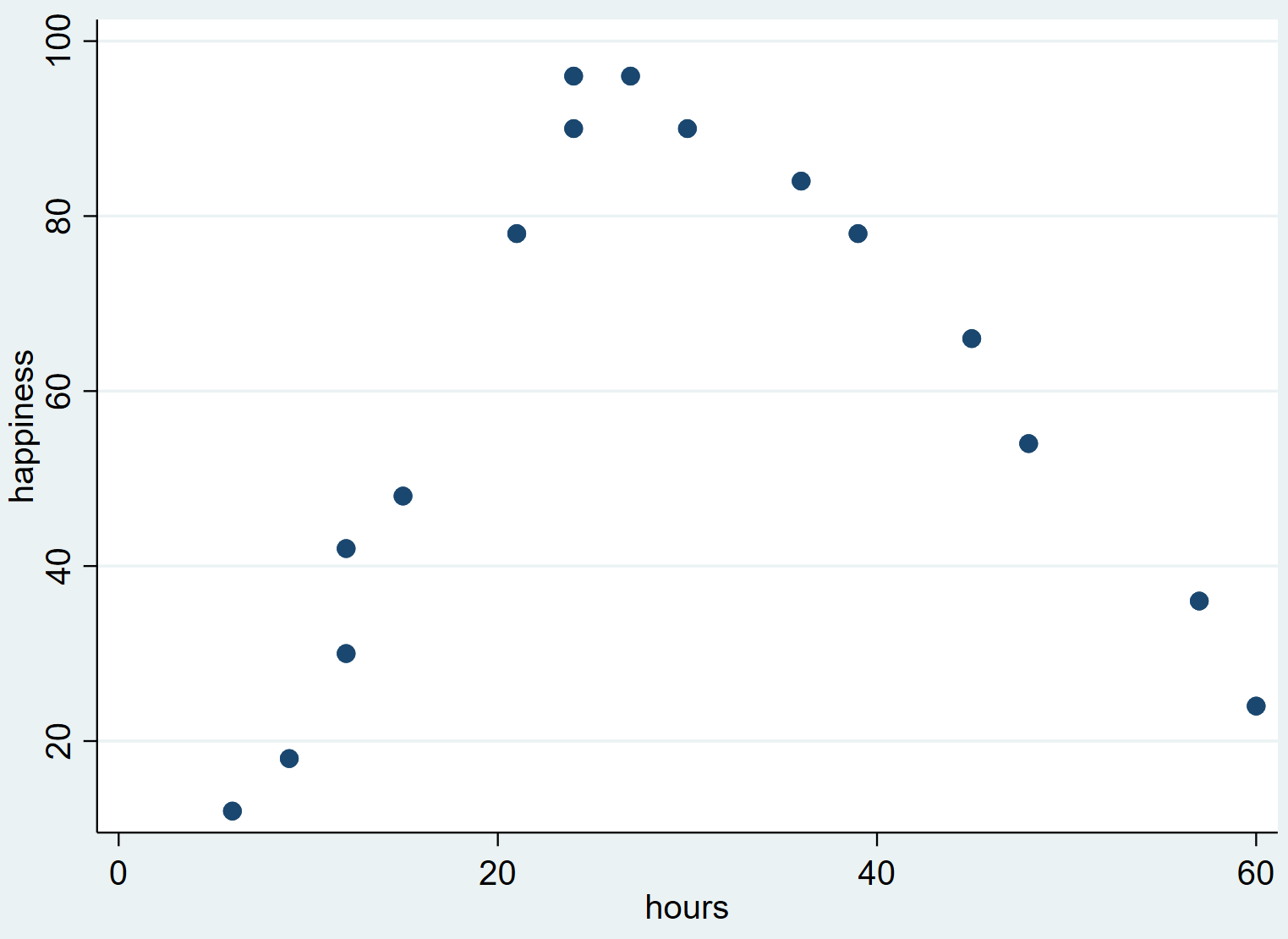
Kita dapat melihat bahwa kebahagiaan cenderung meningkat seiring dengan bertambahnya jumlah jam kerja dari nol hingga titik tertentu, namun kemudian mulai menurun ketika jumlah jam kerja melebihi sekitar 30.

Bentuk “U” terbalik pada diagram sebar menunjukkan bahwa terdapat hubungan kuadrat antara jam kerja dan kebahagiaan, yang berarti kita harus menggunakan regresi kuadrat untuk mengukur hubungan ini.

Langkah 2: Lakukan regresi kuadrat.

Sebelum menyesuaikan model regresi kuadrat ke data, kita perlu membuat variabel baru untuk nilai kuadrat dari variabel prediktor jam kerja kita. Kita dapat melakukan ini dengan mengetikkan yang berikut ini di kotak Command:

gen jam2 = jam*jam

Kita dapat melihat variabel baru ini dengan membuka Data > Editor Data > Editor Data (Jelajahi) dari menu atas.

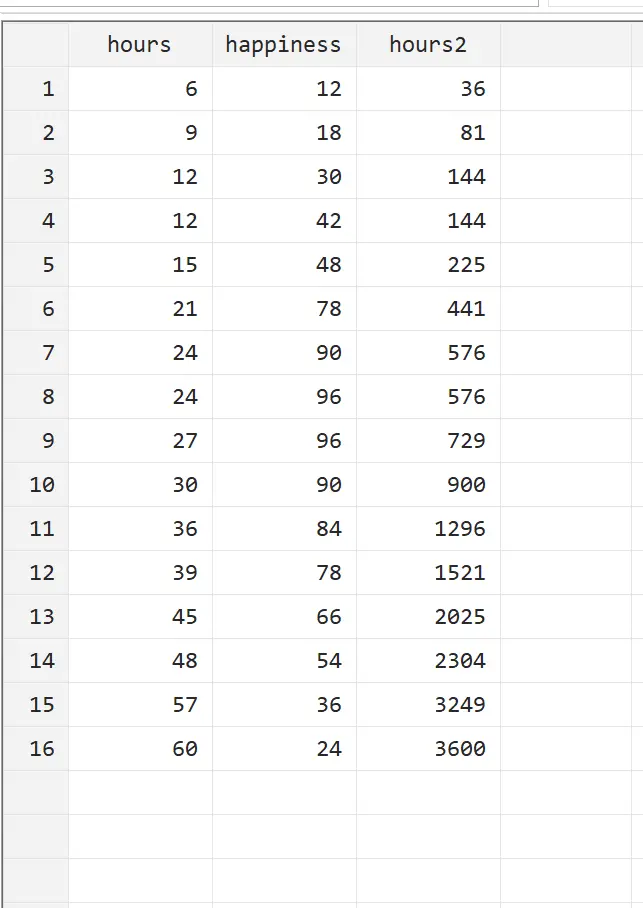
Kita dapat melihat bahwa jam2 hanyalah jam kuadrat. Sekarang kita dapat melakukan regresi kuadrat dengan menggunakan jam dan jam2 sebagai variabel penjelas dan kebahagiaan sebagai variabel respon. Untuk melakukan regresi kuadrat, ketik perintah berikut di kotak Perintah:

jam kemunduran jam kebahagiaan2

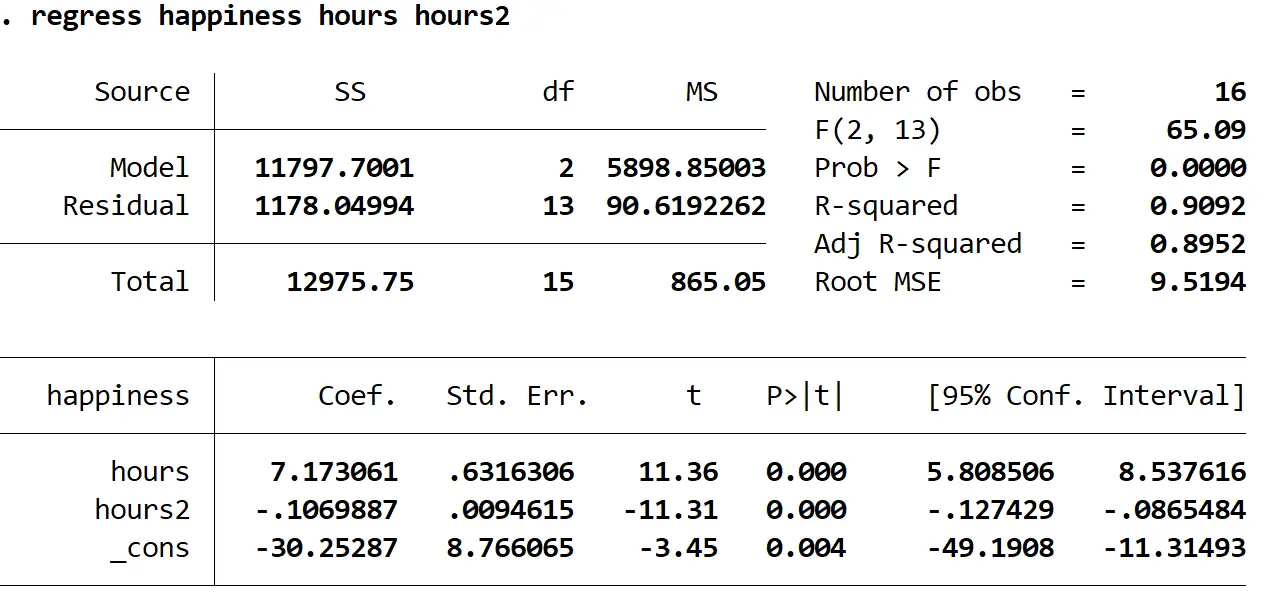
Berikut cara mengartikan angka paling menarik pada hasil:

Masalah > F: 0,000. Ini adalah nilai p untuk regresi keseluruhan. Karena nilai ini kurang dari 0,05, ini berarti gabungan variabel prediktor jam dan jam ² mempunyai hubungan yang signifikan secara statistik dengan variabel respons kebahagiaan .

R kuadrat: 0,9092. Ini adalah proporsi varians variabel respon yang dapat dijelaskan oleh variabel penjelas. Dalam contoh ini, 90,92% variasi kebahagiaan dapat dijelaskan oleh jam dan jam ² .

Persamaan regresi: Kita dapat membentuk persamaan regresi menggunakan nilai koefisien yang ditunjukkan pada tabel keluaran. Dalam hal ini, persamaannya adalah:

prediksi kebahagiaan = -30.25287 + 7.173061 (jam) – 0.1069887 ( ² jam)

Kita dapat menggunakan persamaan ini untuk mengetahui prediksi kebahagiaan seseorang, berdasarkan jumlah jam kerja mereka per minggu.

Misalnya seseorang yang bekerja 60 jam per minggu seharusnya memiliki tingkat kebahagiaan 14,97:

prediksi kebahagiaan = -30.25287 + 7.173061(60) – .1069887(60 ² ) = 14.97 .

Sebaliknya, seseorang yang bekerja 30 jam per minggu seharusnya memiliki tingkat kebahagiaan 88,65:

prediksi kebahagiaan = -30.25287 + 7.173061(30) – .1069887(30 ² ) = 88.65 .

Langkah 3: Laporkan hasilnya.

Terakhir, kami ingin melaporkan hasil regresi kuadrat kami. Berikut ini contoh cara melakukan ini:

Regresi kuadrat dilakukan untuk mengukur hubungan antara jumlah jam kerja seseorang dan tingkat kebahagiaannya (diukur dari 0 hingga 100). Sampel yang digunakan dalam analisis berjumlah 16 orang.

Hasil penelitian menunjukkan bahwa terdapat hubungan yang signifikan secara statistik antara variabel penjelas jam dan jam ² dan variabel respon kebahagiaan (F(2, 13) = 65.09, p <0.0001).

Bersama-sama, kedua variabel penjelas ini menyumbang 90,92% dari variabilitas kebahagiaan yang dijelaskan.

Persamaan regresinya menjadi:

prediksi kebahagiaan = -30.25287 + 7.173061 (jam) – 0.1069887 ( ² jam)