Cara melakukan regresi kuantil di stata

Regresi linier merupakan suatu metode yang dapat kita gunakan untuk memahami hubungan antara satu atau lebih variabel penjelas dan suatu variabel respon.

Biasanya, ketika kita melakukan regresi linier, kita ingin memperkirakan nilai rata-rata variabel respon berdasarkan nilai variabel penjelas. Namun kita dapat memperkirakan mediannya, atau persentil 0,25, atau persentil 0,90, atau persentil lainnya yang kita inginkan.

Di sinilah regresi kuantil berperan. Mirip dengan regresi linier biasa, regresi kuantil membuat persamaan regresi yang memprediksi nilai tertentu (misalnya median, persentil 0,25, persentil 0,90, dll.) untuk variabel respons berdasarkan nilai variabel penjelas.

Tutorial ini menjelaskan cara melakukan regresi kuantil di Stata.

Contoh: regresi kuantil di Stata

Untuk contoh ini, kita akan menggunakan dataset Stata bawaan yang disebut auto . Pertama-tama kita akan memasang model regresi linier dengan menggunakan bobot sebagai variabel prediktor dan mpg sebagai variabel respons. Ini akan memberi tahu kita rata-rata mpg yang diharapkan dari sebuah mobil, berdasarkan bobotnya. Selanjutnya, kami akan menyesuaikan model regresi kuantil untuk memprediksi persentil 0,90 mpg sebuah mobil, berdasarkan bobotnya.

Langkah 1: Muat dan tampilkan data.

Gunakan perintah berikut untuk memuat data:

penggunaan otomatis sistem

Gunakan perintah berikut untuk mendapatkan ringkasan variabel mpg dan bobot:

jumlahkan berat mpg

Langkah 2: Lakukan regresi linier sederhana.

Gunakan perintah berikut untuk melakukan regresi linier sederhana, menggunakan bobot sebagai variabel penjelas dan mpg sebagai variabel respons:

menurunkan berat badan ke mpg

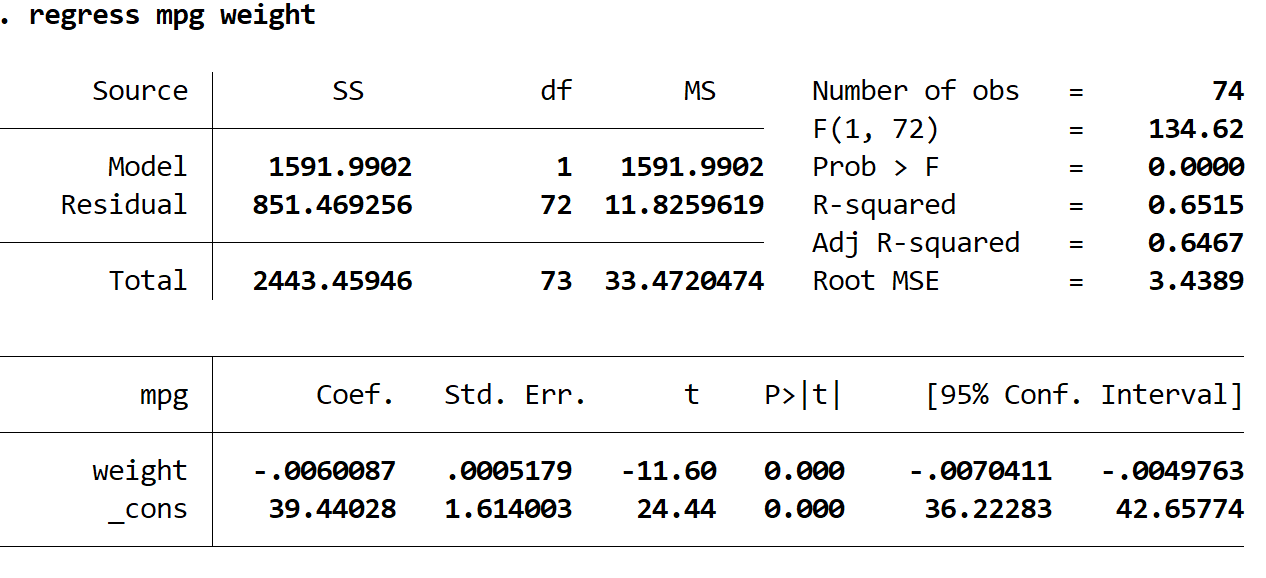
Dari tabel keluaran terlihat bahwa persamaan regresi yang diestimasi adalah:

prediksi mpg = 39,44028 – 0,0060087*(berat)

Kita dapat menggunakan persamaan ini untuk mencari perkiraan mpg rata-rata sebuah mobil, berdasarkan bobotnya. Misalnya, sebuah mobil berbobot 4.000 pon diperkirakan memiliki mpg 15.405:

prediksi mpg = 39,44028 – 0,0060087*(4000) = 15,405

Langkah 3: Lakukan regresi kuantil.

Selanjutnya, mari kita lakukan regresi kuantil untuk mendapatkan perkiraan persentil ^ke-90 dari penghematan bahan bakar sebuah mobil, berdasarkan bobotnya.

Gunakan perintah qreg dengan quantile(0.90) untuk melakukan regresi kuantil ini:

berat qreg mpg, kuantil (0,90)

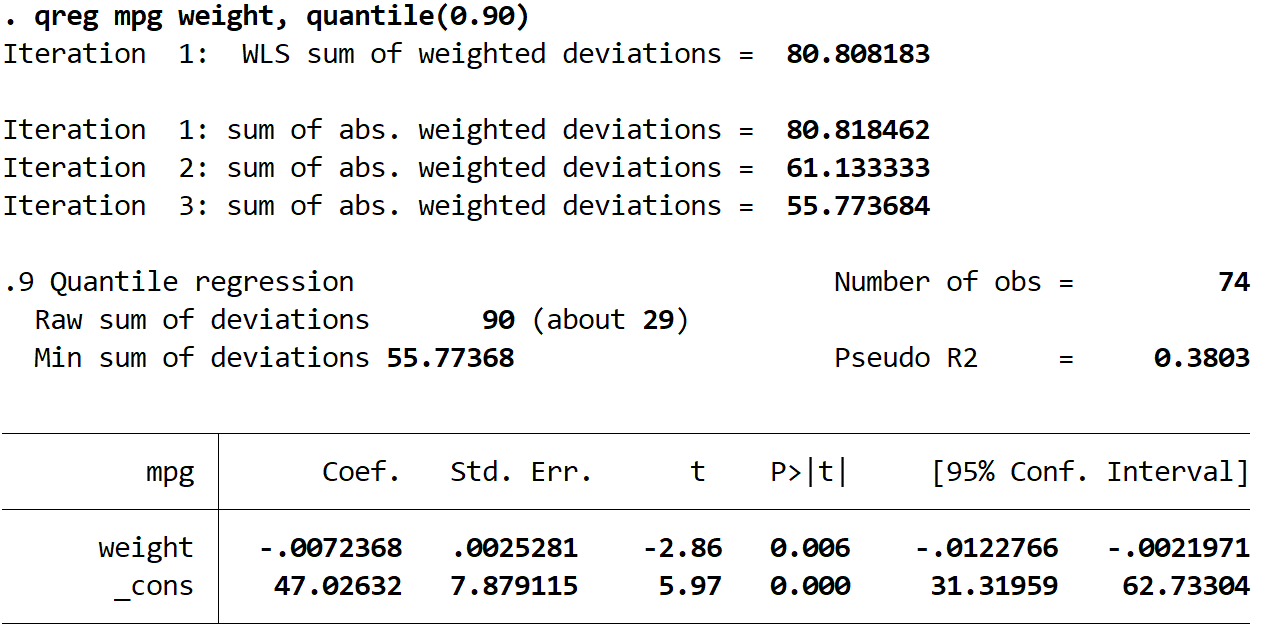
Dari tabel keluaran terlihat bahwa persamaan regresi yang diestimasi adalah:

prediksi persentil ^ke-90 mpg = 47,02632 – 0,0072368*(berat)

Kita dapat menggunakan persamaan ini untuk mencari perkiraannya   mpg untuk mobil pada persentil ^ke-90 , mengingat bobotnya. Misalnya, persentil ^ke-90 mpg untuk mobil berbobot 4.000 pon diperkirakan 18.709:

Prediksi persentil ^ke-90 mpg = 47,02632 – 0,0072368*(4,000) = 18,079

Ingatlah bahwa model regresi linier kita sebelumnya memberi tahu kita bahwa sebuah mobil berbobot 4.000 pon diperkirakan memiliki penghematan bahan bakar rata-rata sebesar 15.405 mpg. Jadi masuk akal jika model regresi kuantil ini memberi tahu kita bahwa sebuah mobil berbobot 4.000 pon perlu menghasilkan 18.079 mpg agar berada di persentil ^ke-90 dari semua mobil dengan bobot tertentu.

Beberapa regresi kuantil sekaligus di Stata

Dimungkinkan juga untuk melakukan beberapa regresi kuantil sekaligus di Stata. Misalnya, kita ingin memperkirakan persentil ^ke-25 , median (misalnya persentil ke- ⁵⁰ ), dan persentil ^ke-90 secara bersamaan.

Untuk melakukan ini, kita dapat menggunakan perintah sqreg dengan perintah q() untuk menentukan kuantil yang akan diperkirakan:

berat mpg sqreg, q (0,25, 0,50, 0,90)

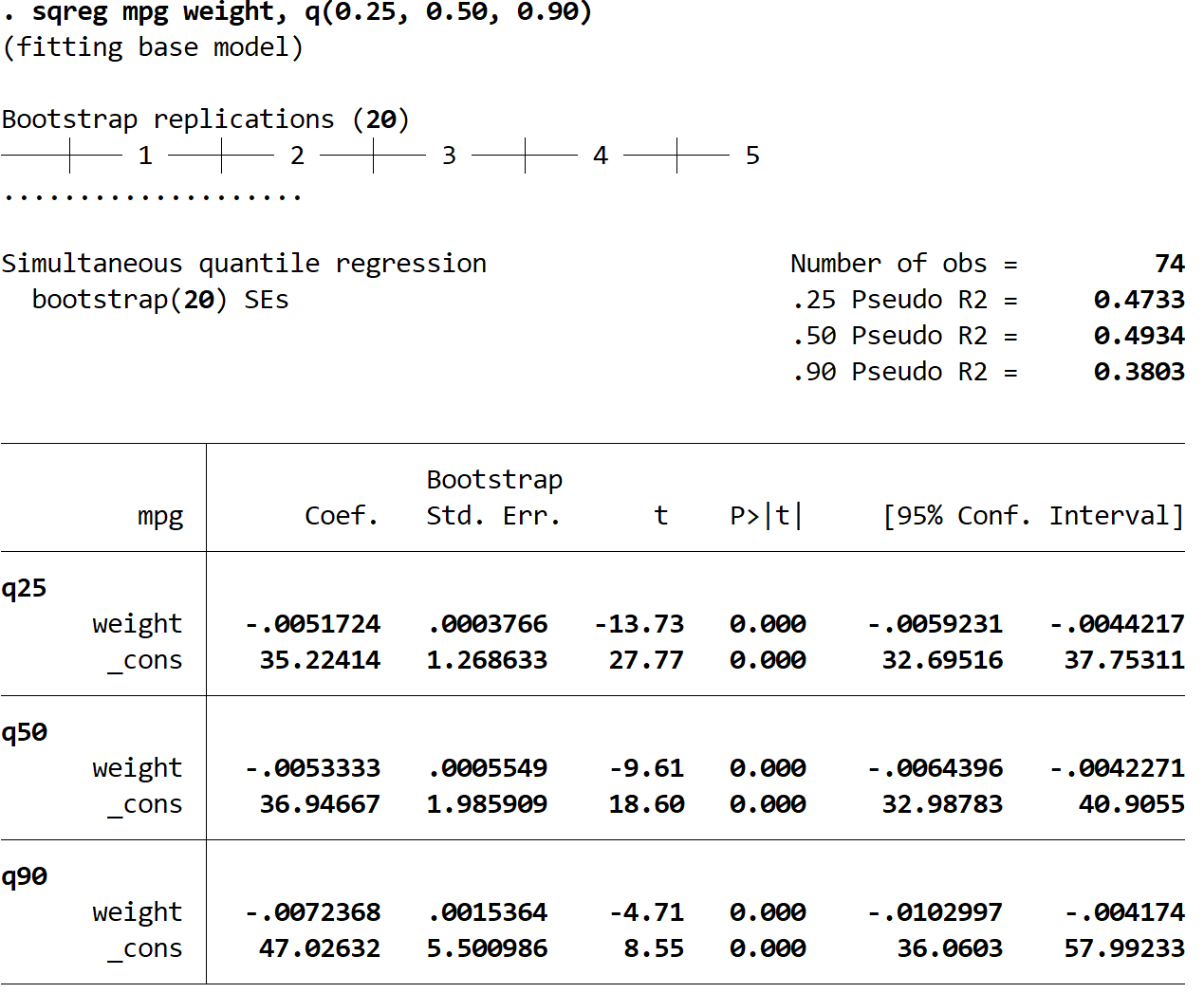
Dengan menggunakan hasil ini, kita dapat membuat estimasi persamaan regresi untuk setiap regresi kuantil:

(1) prediksi mpg persentil ^ke-25 = 35,22414 – 0,0051724*(berat)

(2) prediksi persentil ^ke-50 mpg = 36,94667 – 0,0053333*(berat)

(3) prediksi mpg persentil ^ke-90 = 47,02632 – 0,0072368*(berat)

Sumber daya tambahan

Cara melakukan regresi linier sederhana di Stata
Cara melakukan regresi linier berganda di Stata
Cara melakukan regresi kuadrat di Stata