Cara melakukan regresi hierarki di stata

Regresi hierarki adalah teknik yang dapat kita gunakan untuk membandingkan beberapa model linier yang berbeda.

Ide dasarnya adalah pertama-tama kita menyesuaikan model regresi linier dengan satu variabel penjelas. Selanjutnya, kami menyesuaikan model regresi lain dengan menggunakan variabel penjelas tambahan. Jika R-squared (proporsi varians variabel respon yang dapat dijelaskan oleh variabel penjelas) pada model kedua jauh lebih tinggi dibandingkan R-squared model sebelumnya, berarti model kedua lebih baik.

Kami kemudian mengulangi proses penyesuaian model regresi tambahan dengan variabel yang lebih menjelaskan dan melihat apakah model baru menawarkan peningkatan dibandingkan model sebelumnya.

Tutorial ini memberikan contoh cara melakukan regresi hierarki di Stata.

Contoh: regresi hierarki di Stata

Kami akan menggunakan kumpulan data bawaan yang disebut auto untuk mengilustrasikan cara melakukan regresi hierarki di Stata. Pertama, muat kumpulan data dengan mengetikkan perintah berikut di kotak perintah:

penggunaan otomatis sistem

Kita bisa mendapatkan ringkasan singkat data menggunakan perintah berikut:

untuk meringkas

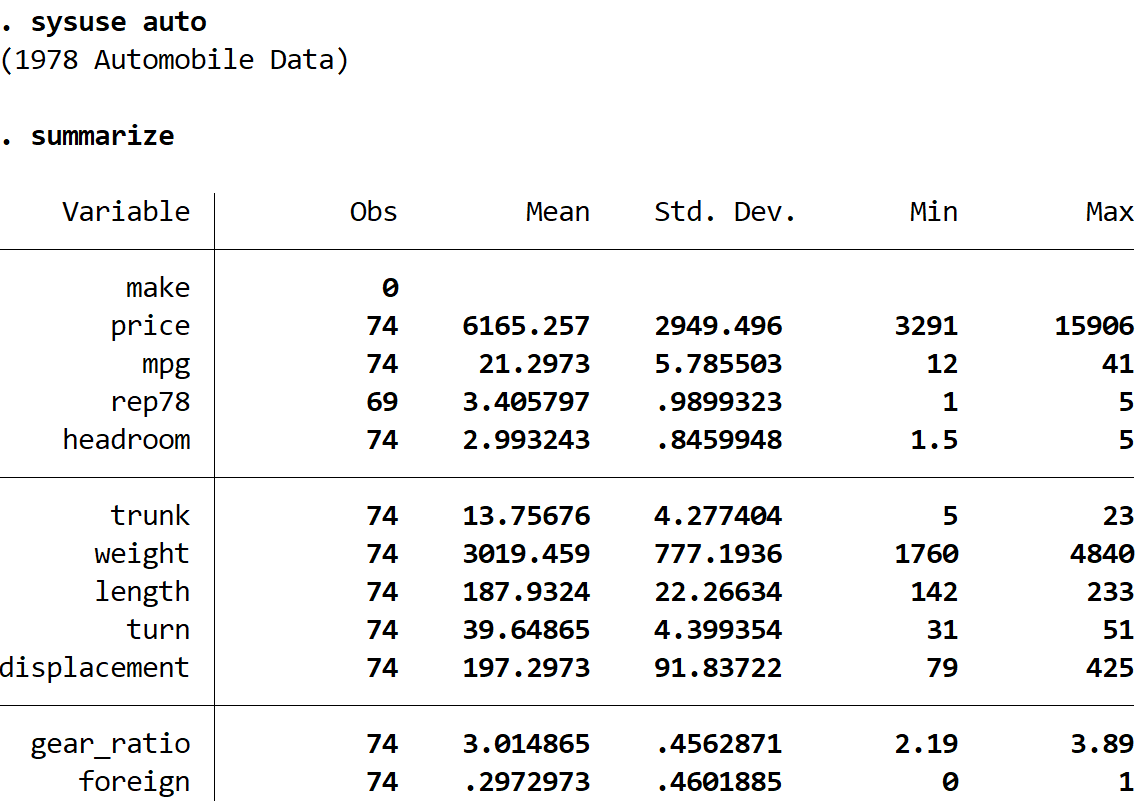
Kita dapat melihat bahwa dataset tersebut berisi informasi tentang 12 variabel berbeda untuk total 74 mobil.

Kami akan menyesuaikan tiga model regresi linier berikut dan menggunakan regresi hierarki untuk melihat apakah setiap model berikutnya memberikan peningkatan yang signifikan dibandingkan model sebelumnya:

Model 1: harga = intersep + mpg

Model 2: harga = intersep + mpg + berat

Model 3: harga = intersep + mpg + berat + rasio roda gigi

Untuk melakukan regresi hierarki di Stata, pertama-tama kita perlu menginstal paket Hireg . Untuk melakukannya, ketikkan yang berikut ini di kotak Perintah:

temukan Hireg

Di jendela yang muncul, klik Hireg dari https://fmwww.bc.edu/RePEc/bocode/h

Di jendela berikutnya, klik tautan yang bertuliskan klik di sini untuk menginstal .

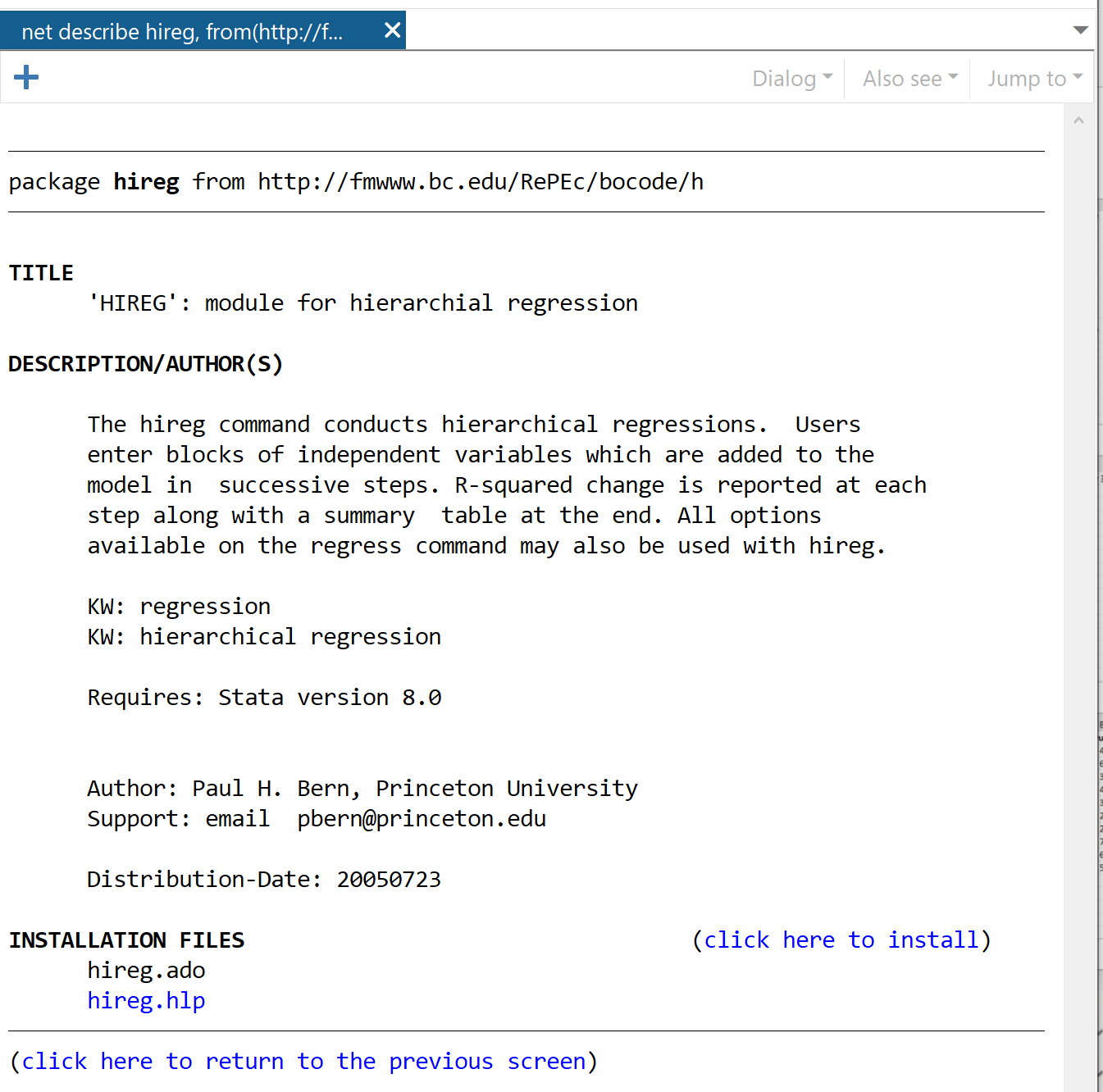
Paket akan diinstal dalam hitungan detik. Kemudian, untuk melakukan regresi hierarki, kita akan menggunakan perintah berikut:

harga sewa (mpg) (berat) (gear_ratio)

Inilah yang diminta Stata untuk dilakukan:

• Lakukan regresi hierarki menggunakan harga sebagai variabel respon di setiap model.
• Untuk model pertama, gunakan mpg sebagai variabel penjelas.
• Untuk model kedua, tambahkan bobot sebagai variabel penjelas tambahan.
• Untuk model ketiga, tambahkan gear_ratio sebagai variabel penjelas lainnya.

Berikut hasil model pertama:

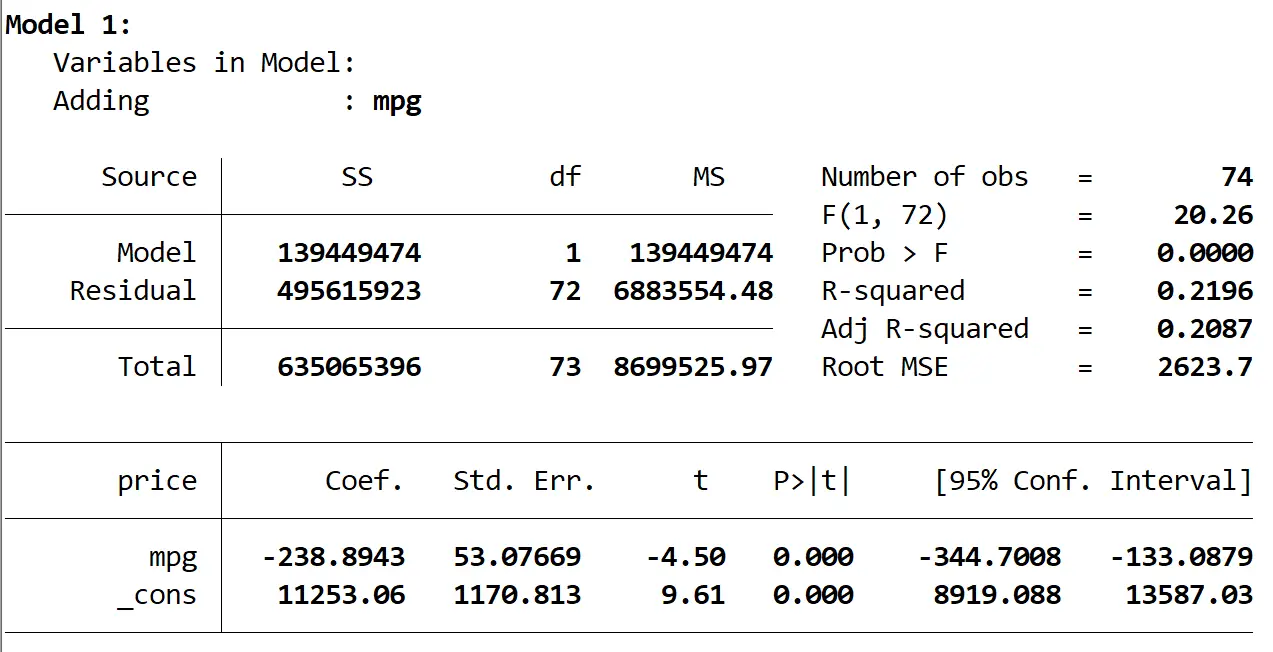
Kita melihat bahwa R-kuadrat model adalah 0,2196 dan nilai p keseluruhan (Prob > F) model adalah 0,0000 , yang signifikan secara statistik pada α = 0,05.

Selanjutnya kita lihat hasil model kedua:

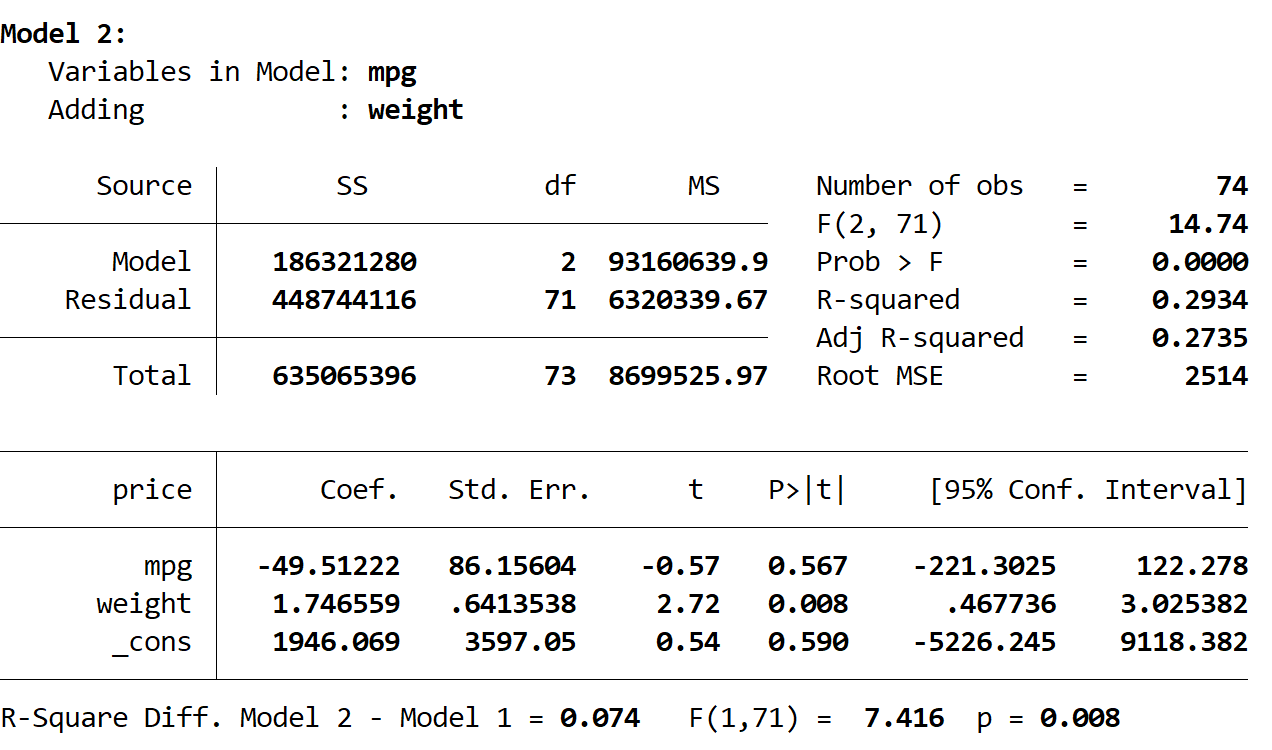
R kuadrat model ini adalah 0,2934 , lebih besar dari model pertama. Untuk menentukan apakah perbedaan ini signifikan secara statistik, Stata melakukan uji F yang memberikan angka berikut di bagian bawah hasil:

• Selisih R kuadrat antara kedua model = 0,074
• F statistik untuk selisih = 7,416
• Nilai p yang sesuai dari statistik F = 0,008

Karena nilai p kurang dari 0,05, kami menyimpulkan bahwa terdapat peningkatan yang signifikan secara statistik pada model kedua dibandingkan model pertama.

Terakhir, kita bisa melihat hasil dari model ketiga:

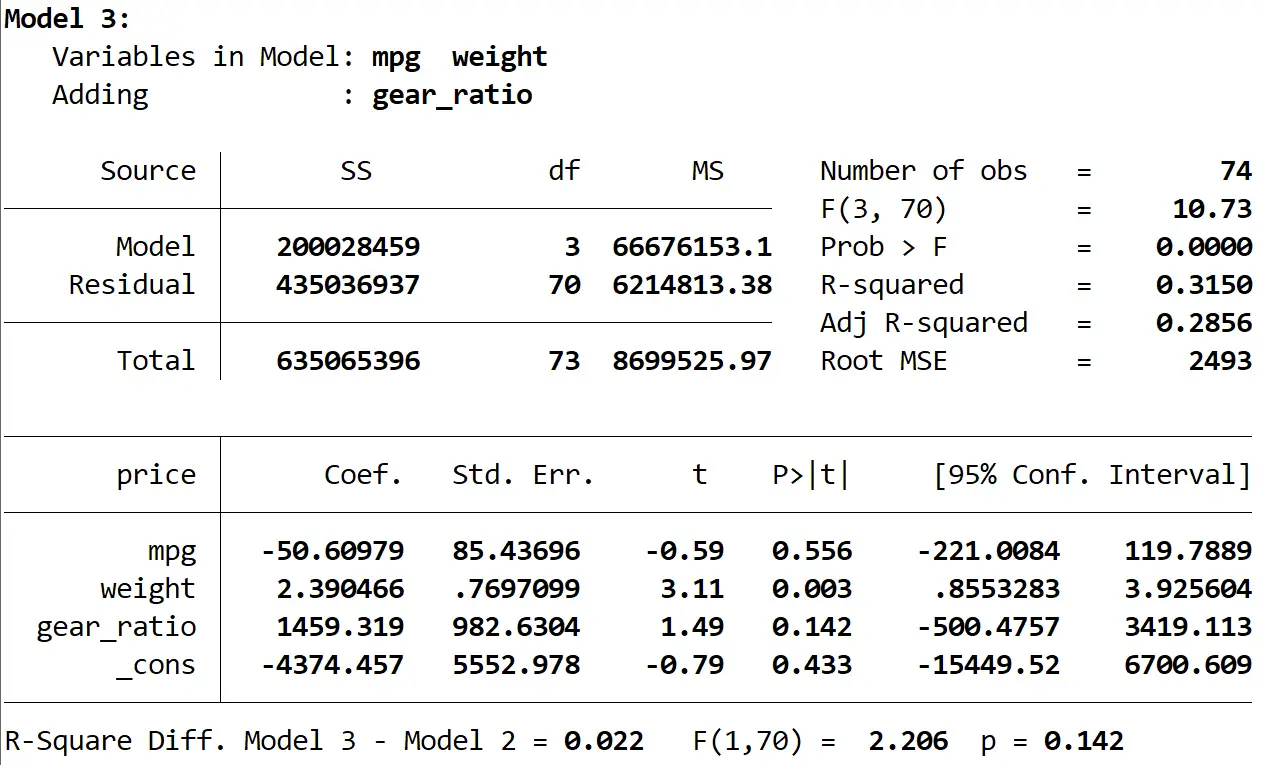
R kuadrat model ini adalah 0,3150 , lebih besar dari model kedua. Untuk menentukan apakah perbedaan ini signifikan secara statistik, Stata melakukan uji F yang memberikan angka berikut di bagian bawah hasil:

• Selisih R kuadrat antara kedua model = 0,022
• F statistik untuk selisih = 2,206
• Nilai p yang sesuai dari statistik F = 0,142

Karena nilai p tidak kurang dari 0,05, kami tidak memiliki cukup bukti untuk mengatakan bahwa model ketiga memberikan peningkatan dibandingkan model kedua.

Di akhir hasil, kita dapat melihat bahwa Stata memberikan ringkasan hasil:

Dalam contoh khusus ini, kita dapat menyimpulkan bahwa Model 2 menawarkan peningkatan yang signifikan dibandingkan Model 1, namun Model 3 tidak menawarkan peningkatan yang signifikan dibandingkan Model 2.