Cara melakukan uji tren mann-kendall di r
Uji tren Mann-Kendall digunakan untuk mengetahui ada atau tidaknya tren pada data deret waktu. Ini adalah uji non-parametrik, artinya tidak ada asumsi mendasar yang dibuat mengenai normalitas data.
Hipotesis pengujiannya adalah sebagai berikut:
H 0 (hipotesis nol): tidak ada tren dalam data.
H A (hipotesis alternatif): Ada tren dalam data. (Ini bisa menjadi tren positif atau negatif)
Jika nilai p pengujian berada di bawah tingkat signifikansi tertentu (pilihan umum adalah 0,10, 0,05, dan 0,01), maka terdapat bukti signifikan secara statistik bahwa terdapat tren dalam data dari rangkaian waktu.
Tutorial ini menjelaskan cara melakukan uji tren Mann-Kendall di R.
Contoh: Uji tren Mann-Kendall di R
Untuk melakukan uji tren Mann-Kendall di R, kita akan menggunakan fungsi MannKendall() dari perpustakaan Kendall , yang menggunakan sintaks berikut:
MannKendall(x)
Emas:
- x = vektor data, seringkali berupa deret waktu
Untuk mengilustrasikan cara melakukan pengujian, kami akan menggunakan kumpulan data PrecipGL bawaan Perpustakaan Kendall , yang berisi informasi curah hujan tahunan untuk semua Great Lakes dari tahun 1900 hingga 1986:
#load Kendall library and PrecipGL dataset library(Kendall) data(PrecipGL) #view dataset PrecipGL Time Series: Start = 1900 End = 1986 Frequency = 1 [1] 31.69 29.77 31.70 33.06 31.31 32.72 31.18 29.90 29.17 31.48 28.11 32.61 [13] 31.31 30.96 28.40 30.68 33.67 28.65 30.62 30.21 28.79 30.92 30.92 28.13 [25] 30.51 27.63 34.80 32.10 33.86 32.33 25.69 30.60 32.85 30.31 27.71 30.34 [37] 29.14 33.41 33.51 29.90 32.69 32.34 35.01 33.05 31.15 36.36 29.83 33.70 [49] 29.81 32.41 35.90 37.45 30.39 31.15 35.75 31.14 30.06 32.40 28.44 36.38 [61] 31.73 31.27 28.51 26.01 31.27 35.57 30.85 33.35 35.82 31.78 34.25 31.43 [73] 35.97 33.87 28.94 34.62 31.06 38.84 32.25 35.86 32.93 32.69 34.39 33.97 [85] 32.15 40.16 36.32 attr(,"title") [1] Annual precipitation, 1900-1986, Entire Great Lakes
Untuk melihat apakah ada tren pada data, kita dapat melakukan uji tren Mann-Kendall:
#Perform the Mann-Kendall Trend Test
MannKendall(PrecipGL)
tau = 0.265, 2-sided pvalue = 0.00029206
Statistik ujinya adalah 0,265 dan nilai p dua sisi yang sesuai adalah 0,00029206 . Karena nilai p ini kurang dari 0,05, kami akan menolak hipotesis nol dari pengujian tersebut dan menyimpulkan bahwa terdapat tren dalam data.
Untuk memvisualisasikan tren, kita dapat membuat plot waktu curah hujan tahunan per tahun dan menambahkan garis halus untuk mewakili tren tersebut:
#Plot the time series data plot(PrecipGL) #Add a smooth line to visualize the trend lines(lowess(time(PrecipGL),PrecipGL), col='blue')
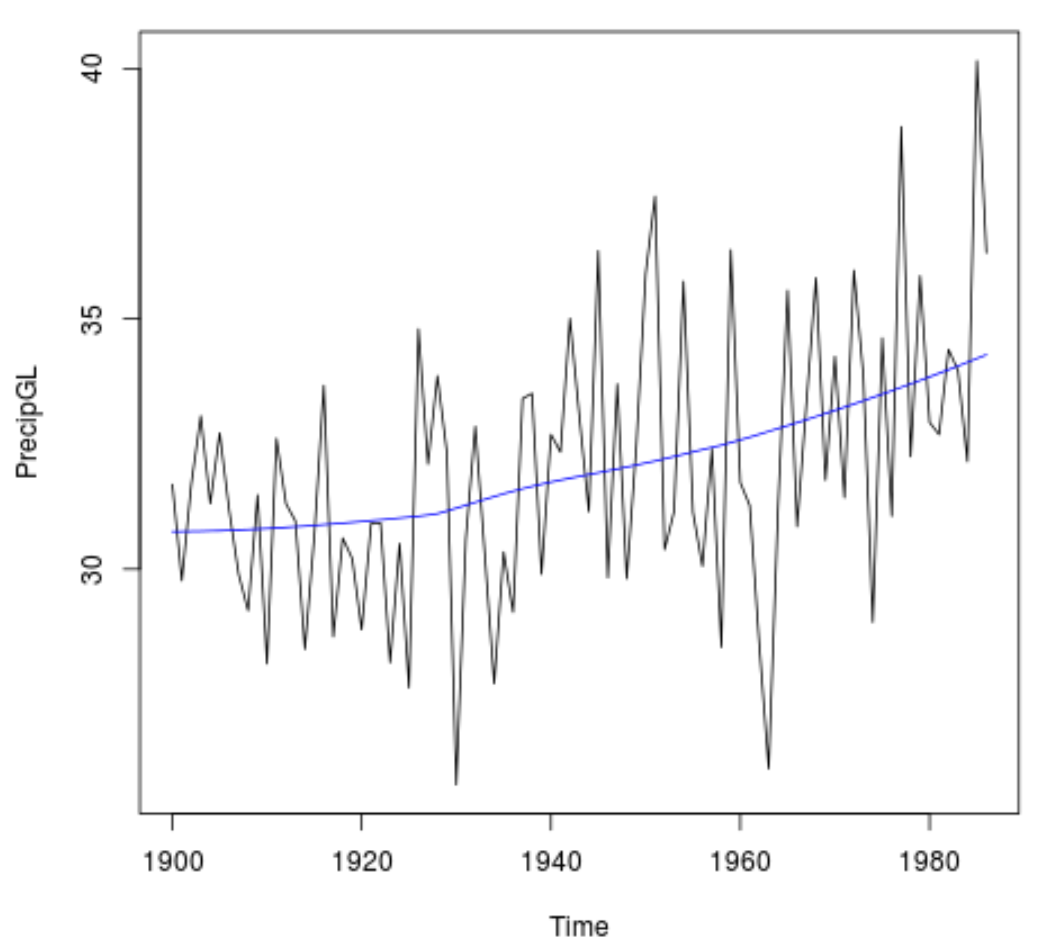
Perhatikan bahwa kita juga dapat melakukan uji tren Mann-Kendall yang disesuaikan secara musiman untuk memperhitungkan setiap musiman dalam data menggunakan perintah SeasonalMannKendall(x) :
#Perform a seasonally-adjusted Mann-Kendall Trend Test
SeasonalMannKendall(PrecipGL)
tau = 0.265, 2-sided pvalue = 0.00028797
Statistik ujinya adalah 0,265 dan nilai p dua sisi yang sesuai adalah 0,00028797 . Sekali lagi nilai p ini kurang dari 0,05, jadi kami akan menolak hipotesis nol dari pengujian tersebut dan menyimpulkan bahwa terdapat tren dalam data.