Pengenalan distribusi binomial
Distribusi binomial adalah salah satu distribusi yang paling populer dalam statistik. Untuk memahami distribusi binomial, ada baiknya memahami terlebih dahulu eksperimen binomial .
Eksperimen binomial
Eksperimen binomial adalah eksperimen yang mempunyai sifat-sifat sebagai berikut:
- Percobaan terdiri dari n percobaan berulang.
- Setiap percobaan hanya memiliki dua kemungkinan hasil.
- Probabilitas keberhasilan, dilambangkan dengan p , adalah sama untuk setiap percobaan.
- Setiap tes bersifat independen.
Contoh paling jelas dari percobaan binomial adalah pelemparan koin. Misalnya kita melempar sebuah koin sebanyak 10 kali. Ini adalah eksperimen binomial karena mempunyai empat sifat berikut:
- Percobaan terdiri dari n percobaan berulang – Ada 10 percobaan.
- Setiap percobaan hanya memiliki dua kemungkinan hasil: kepala atau ekor.
- Probabilitas keberhasilan, dilambangkan dengan p , adalah sama untuk setiap percobaan. Jika kita mendefinisikan “sukses” sebagai pendaratan, maka probabilitas keberhasilan adalah tepat 0,5 untuk setiap percobaan.
- Setiap percobaan bersifat independen – Hasil dari satu pelemparan koin tidak mempengaruhi hasil pelemparan koin lainnya.
Distribusi binomial
Distribusi binomial menggambarkan probabilitas diperolehnya k keberhasilan dalam n percobaan binomial.
Jika suatu variabel acak X mengikuti distribusi binomial, maka peluang keberhasilan X = k dapat dicari dengan rumus berikut:
P(X=k) = n C k * p k * (1-p) nk
Emas:
- n: jumlah percobaan
- k: jumlah keberhasilan
- p: probabilitas keberhasilan pada percobaan tertentu
- n C k : banyaknya cara untuk memperoleh k keberhasilan dalam n percobaan
Misalnya kita melempar sebuah koin sebanyak 3 kali. Kita dapat menggunakan rumus di atas untuk menentukan peluang munculnya gambar 0, 1, 2, dan 3 pada 3 pelemparan berikut:
P(X=0) = 3 C 0 * 0,5 0 * (1-0,5) 3-0 = 1 * 1 * (0,5) 3 = 0,125
P(X=1) = 3 C 1 * 0,5 1 * (1-0,5) 3-1 = 3 * 0,5 * (0,5) 2 = 0,375
P(X=2) = 3 C 2 * 0,5 2 * (1-0,5) 3-2 = 3 * 0,25 * (0,5) 1 = 0,375
P(X=3) = 3 C 3 * 0,5 3 * (1-0,5) 3-3 = 1 * 0,125 * (0,5) 0 = 0,125
Catatan : Kami menggunakan kalkulator gabungan ini untuk menghitung nCk untuk setiap contoh.
Kita dapat membuat histogram sederhana untuk memvisualisasikan distribusi probabilitas ini:
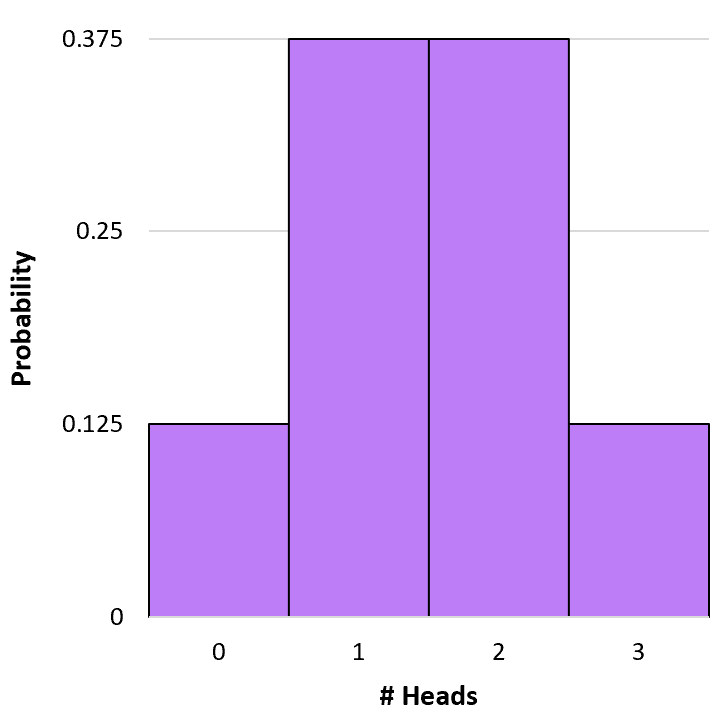
Perhitungan probabilitas binomial kumulatif
Menghitung probabilitas binomial tunggal sangatlah mudah (misalnya probabilitas munculnya koin 1 kali dari 3 pelemparan) dengan menggunakan rumus di atas, namun untuk menghitung probabilitas binomial kumulatif kita perlu menambahkan probabilitas individu.
Misalnya, kita ingin mengetahui probabilitas munculnya sebuah koin sebanyak 1 kali atau kurang dari 3 kali pelemparan. Kami akan menggunakan rumus berikut untuk menghitung probabilitas ini:
P(X≤1) = P(X=0) + P(X=1) = 0,125 + 0,375 = 0,5 .
Ini disebut probabilitas kumulatif karena melibatkan penambahan beberapa probabilitas. Kita dapat menghitung probabilitas kumulatif untuk mendapatkan k kepala atau lebih sedikit untuk setiap hasil menggunakan rumus serupa:
P(X≤0) = P(X=0) = 0,125 .
P(X≤1) = P(X=0) + P(X=1) = 0,125 + 0,375 = 0,5 .
P(X≤2) = P(X=0) + P(X=1) + P(X=2) = 0,125 + 0,375 + 0,375 = 0,875 .
P(X≤3) = P(X=0) + P(X=1) + P(X=2) + P(X=3) = 0,125 + 0,375 + 0,375 + 0,125 = 1 .
Kita dapat membuat histogram untuk memvisualisasikan distribusi probabilitas kumulatif ini:
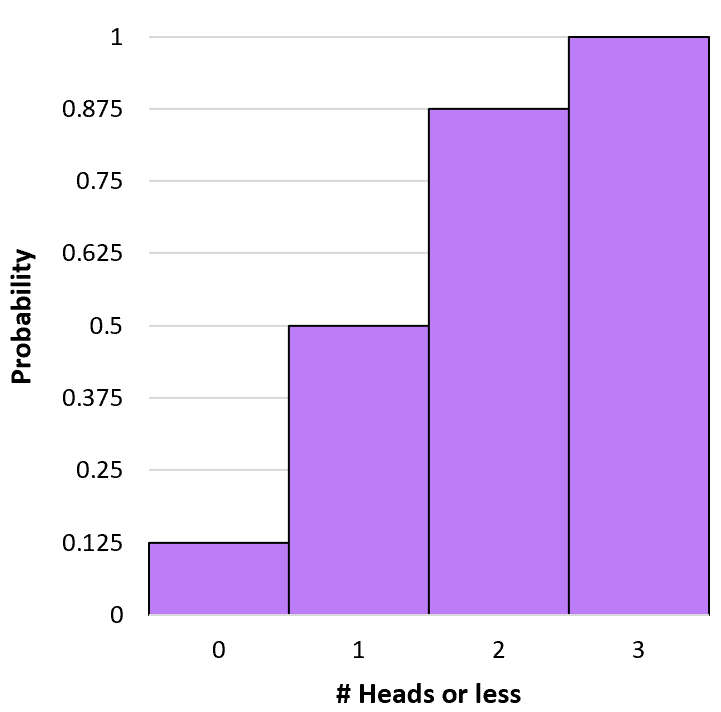
Kalkulator Probabilitas Binomial
Ketika kita bekerja dengan angka-angka kecil (misalnya pelemparan 3 koin), masuk akal untuk menghitung probabilitas binomial dengan tangan. Namun, ketika kita bekerja dengan angka yang lebih besar (misalnya 100 kali seri), akan sulit untuk menghitung probabilitasnya dengan tangan. Dalam kasus ini, akan sangat membantu jika menggunakan kalkulator probabilitas binomial seperti di bawah ini.
Sebagai contoh, misalkan kita melempar sebuah koin n = 100 kali, peluang koin tersebut mengenai kepala dalam suatu percobaan tertentu adalah p = 0,5, dan kita ingin mengetahui probabilitas koin tersebut mengenai kepala k = 43 kali atau kurang:
P(X= 43 ) = 0,03007
P(X< 43 ) = 0,06661
P( X≤43 ) = 0,09667
P(X> 43 ) = 0,90333
P( X≥43 ) = 0,93339
Berikut cara menafsirkan hasilnya:
- Peluang munculnya koin tepat sebanyak 43 kali adalah 0,03007 .
- Peluang munculnya koin kurang dari 43 kali adalah 0,06661 .
- Peluang munculnya koin sebanyak 43 kali atau kurang adalah 0,09667 .
- Peluang munculnya koin lebih dari 43 kali adalah 0,90333 .
- Peluang munculnya koin sebanyak 43 kali atau lebih adalah 0,93339 .
Sifat-sifat distribusi binomial
Distribusi binomial mempunyai sifat-sifat sebagai berikut:
Rata-rata distribusinya adalah μ = np
Varians distribusinya adalah σ 2 = np(1-p)
Simpangan baku distribusinya adalah σ = √ np(1-p)
Misalnya kita melempar sebuah uang logam sebanyak 3 kali. Misal p = peluang koin mendarat di kepala.
Jumlah rata-rata kepala yang kami harapkan adalah μ = np = 3*.5 = 1.5 .
Varians jumlah kepala yang kami harapkan adalah σ 2 = np(1-p) = 3*.5*(1-.5) = 0.75 .
Soal Praktek Distribusi Binomial
Gunakan soal latihan berikut untuk menguji pengetahuan Anda tentang distribusi binomial.
Masalah 1
Pertanyaan: Bob melakukan 60% percobaan lemparan bebasnya. Jika dia melakukan 12 lemparan bebas, berapakah peluang dia berhasil tepat 10 lemparan bebas?
Jawaban: Dengan menggunakan kalkulator distribusi binomial di atas dengan p = 0,6, n = 12 dan k = 10, diperoleh P(X=10) = 0,06385 .
Masalah 2
Pertanyaan: Jessica melempar koin sebanyak 5 kali. Berapa peluang munculnya koin tersebut sebanyak 2 kali atau kurang?
Jawaban: Dengan menggunakan kalkulator distribusi binomial di atas dengan p = 0,5, n = 5 dan k = 2, kita peroleh bahwa P(X≤2) = 0,5 .
Masalah 3
Pertanyaan: Peluang seorang siswa tertentu diterima di perguruan tinggi tertentu adalah 0,2. Jika ada 10 mahasiswa yang mendaftar, berapa peluang diterima lebih dari 4 mahasiswa?
Jawaban: Dengan menggunakan kalkulator distribusi binomial di atas dengan p = 0,2, n = 10 dan k = 4, kita peroleh bahwa P(X>4) = 0,03279 .
Masalah 4
Pertanyaan: Anda melempar koin sebanyak 12 kali. Berapa perkiraan jumlah rata-rata kepala yang akan muncul?
Jawaban: Ingatlah bahwa rata-rata distribusi binomial dihitung sebagai μ = np. Jadi, μ = 12*0.5 = 6 kepala .
Masalah 5
Pertanyaan: Mark melakukan home run pada 10% percobaannya. Jika dia melakukan 5 kali percobaan dalam suatu permainan, berapakah selisih jumlah home run yang dia lakukan?
Jawaban: Ingatlah bahwa varians distribusi binomial dihitung sebagai σ 2 = np(1-p). Jadi, σ2 = 6*.1*(1-.1) = 0.54 .
Sumber daya tambahan
Artikel berikut dapat membantu Anda mempelajari cara menggunakan distribusi binomial dalam berbagai perangkat lunak statistik:
- Cara Menghitung Probabilitas Binomial di Excel
- Cara Menghitung Probabilitas Binomial pada Kalkulator TI-84
- Cara menghitung probabilitas binomial di R
- Cara memplot distribusi binomial di R