Bagaimana menerapkan teorema chebyshev di excel
Teorema Chebyshev menyatakan bahwa untuk bilangan apa pun k yang lebih besar dari 1, setidaknya 1 – 1/k 2 dari nilai data dalam setiap distribusi terlatih terletak dalam k standar deviasi dari mean.
Misalnya, untuk distribusi berbentuk apa pun, setidaknya 1 – 1/3 2 = 88,89% nilai dalam distribusi akan berada dalam 3 standar deviasi mean.
Tutorial ini menunjukkan beberapa contoh penerapan teorema Chebyshev di Excel.
Contoh 1: Gunakan teorema Chebyshev untuk menentukan berapa persentase nilai yang berada antara 30 dan 70 untuk kumpulan data dengan rata-rata 50 dan deviasi standar 10.
Pertama, tentukan nilai k. Kita dapat melakukannya dengan menentukan berapa standar deviasi antara 30 dan 70 dari mean:
(30 – mean) / simpangan baku = (30 – 50) / 10 = -20 / 10 = -2
(70 – mean) / simpangan baku = (70 – 50) / 10 = 20/10 = 2
Nilai 30 dan 70 masing-masing merupakan 2 standar deviasi di bawah dan di atas mean. Jadi, k = 2 .
Kita kemudian dapat menggunakan rumus berikut di Excel untuk menemukan persentase minimum nilai yang berada dalam 2 standar deviasi dari mean kumpulan data ini:
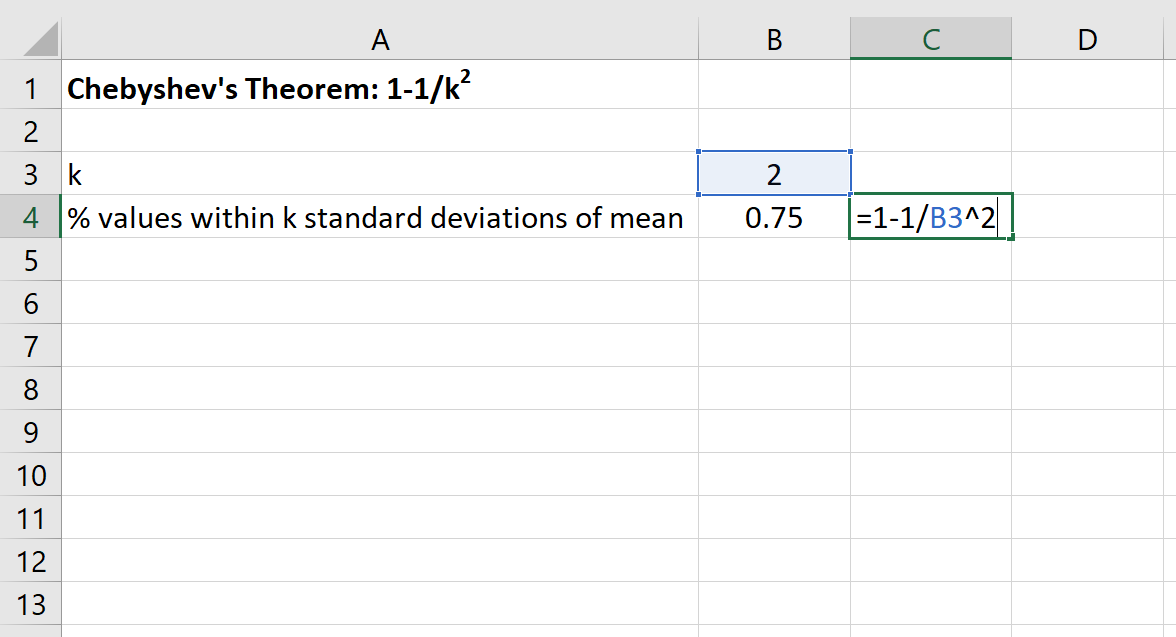
Persentase nilai antara 30 dan 70 untuk kumpulan data ini setidaknya 75% .
Contoh 2: Gunakan teorema Chebyshev untuk menentukan berapa persentase nilai yang berada antara 20 dan 50 untuk kumpulan data dengan rata-rata 35 dan deviasi standar 5.
Pertama, tentukan nilai k. Kita dapat melakukannya dengan menentukan berapa standar deviasi antara 20 dan 50 dari mean:
(20 – mean) / simpangan baku = (20 – 35) / 5 = -15 / 5 = -3
(50 – mean) / simpangan baku = (50 – 35) / 5 = 15 / 5 = 3
Nilai 20 dan 50 masing-masing merupakan 3 standar deviasi di bawah dan di atas mean. Jadi, k = 3 .
Kita kemudian dapat menggunakan rumus berikut di Excel untuk menemukan persentase minimum nilai yang berada dalam 3 standar deviasi dari mean kumpulan data ini:
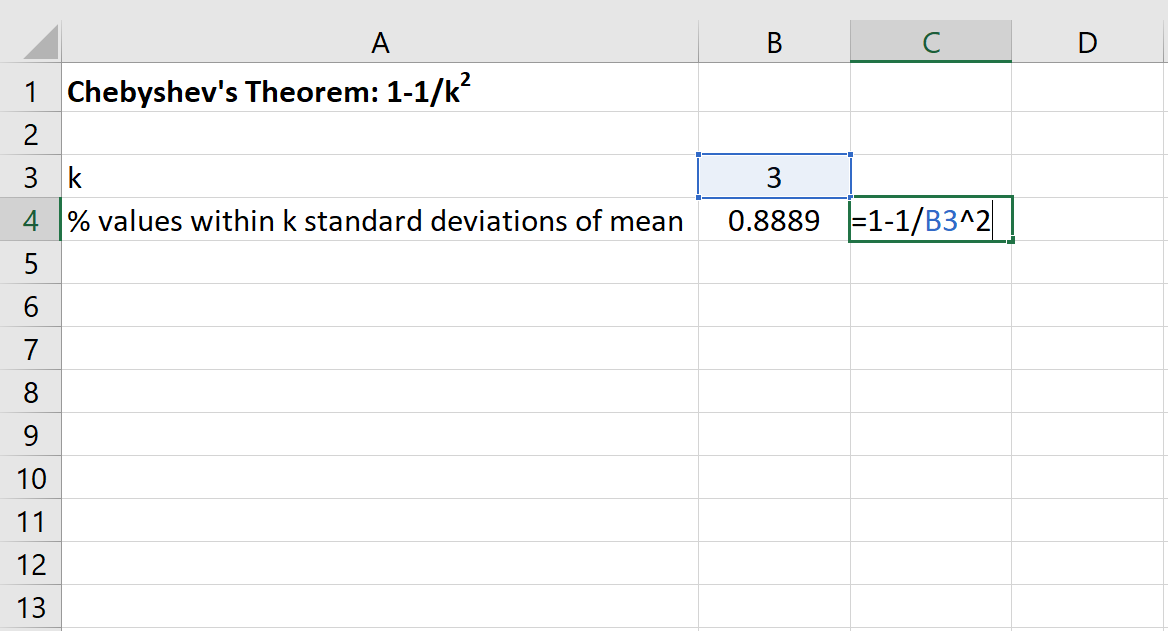
Persentase nilai antara 20 dan 50 untuk kumpulan data ini setidaknya 88,89% .
Contoh 3: Gunakan teorema Chebyshev untuk menentukan berapa persentase nilai yang berada antara 80 dan 120 untuk kumpulan data dengan rata-rata 100 dan deviasi standar 5.
Pertama, tentukan nilai k. Kita dapat melakukannya dengan menentukan berapa standar deviasi antara 80 dan 120 dari mean:
(80 – mean) / simpangan baku = (80 – 100) / 5 = -20 / 5 = -4
(120 – mean) / simpangan baku = (120 – 100) / 5 = 20 / 5 = 4
Nilai 80 dan 120 masing-masing merupakan 4 standar deviasi di bawah dan di atas mean. Jadi, k = 4 .
Kita kemudian dapat menggunakan rumus berikut di Excel untuk menemukan persentase minimum nilai yang berada dalam 4 standar deviasi dari mean kumpulan data ini:
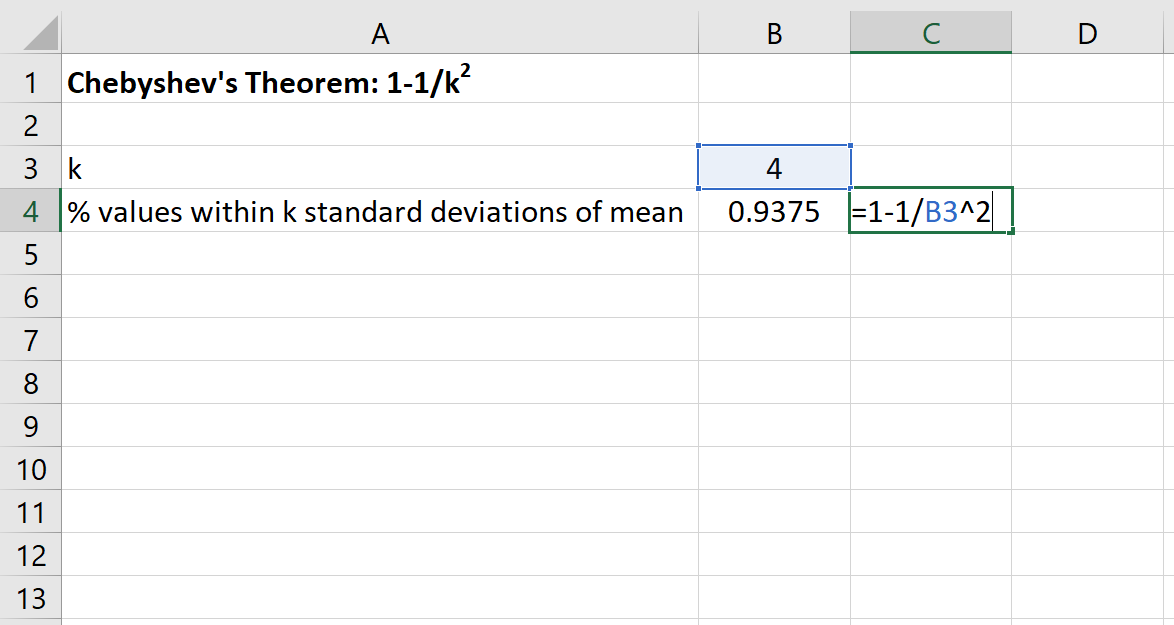
Persentase nilai antara 80 dan 120 untuk kumpulan data ini setidaknya adalah 93,75% .