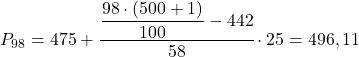Persentil (statistik)

Oleh Benjamin anderson Agustus 5, 2023 Statistik 0 Komentar

Artikel ini menjelaskan apa itu persentil dan cara menghitungnya. Anda akan menemukan latihan persentil yang terselesaikan dan, sebagai tambahan, Anda akan dapat menghitung persentil mana pun dari sampel data Anda dengan kalkulator online.

Apa itu persentil?

Dalam statistik, persentil adalah nilai yang membagi sekumpulan data terurut menjadi seratus bagian yang sama. Jadi, persentil menunjukkan nilai di bawah persentase kumpulan data.

Misalnya, nilai persentil ke-35 lebih tinggi dari 35% data observasi, namun lebih rendah dibandingkan data lainnya.

Persentil dilambangkan dengan huruf kapital P dan indeks persentil, yaitu persentil ke-1 adalah P ₁ , persentil ke-40 adalah P ₄₀ , persentil ke-79 adalah P ₇₉ , dan seterusnya.

👉 Anda dapat menggunakan kalkulator di bawah ini untuk menghitung persentil kumpulan data apa pun.

Demikian pula, persentil adalah ukuran posisi non-pusat bersama dengan kuartil, kuintil, dan desil. Anda dapat memeriksa arti dari masing-masing jenis kuantil ini di situs web kami.

Perlu diperhatikan bahwa istilah persentil juga digunakan untuk membandingkan berat dan tinggi badan bayi dengan nilai standar bayi lainnya, karena terdapat tabel pertumbuhan dengan nilai tercatat yang membantu menentukan apakah bayi tumbuh dengan baik atau tidak. . .

Cara menghitung persentil

Untuk menghitung posisi persentil suatu rangkaian data statistik, Anda harus mengalikan angka persentil dengan jumlah total jumlah titik data ditambah satu dan membagi hasilnya dengan seratus.

Oleh karena itu, rumus persentilnya adalah:

$\cfrac{k\cdot (n+1)}{100} \qquad k=1, 2, 3,\ldots ,97,98,99$

Harap diperhatikan: rumus ini memberi tahu kita posisi persentil, tetapi tidak menunjukkan nilainya. Persentilnya adalah data yang terletak pada posisi yang diperoleh rumus.

Namun terkadang hasil rumus ini akan memberikan kita angka desimal, oleh karena itu kita harus membedakan dua kasus tergantung apakah hasilnya berupa angka desimal atau bukan:

Jika hasil rumusnya berupa angka tanpa bagian desimal , maka persentilnya sesuai dengan data yang berada pada posisi yang disediakan rumus di atas.
Jika hasil rumusnya berupa angka dengan bagian desimal , maka nilai persentil pastinya dihitung menggunakan rumus berikut:

$P=x_i+d\cdot (x_{i+1}-x_i)$

Dimana x _i dan x _i+1 adalah bilangan posisi di mana letak bilangan yang diperoleh rumus pertama, dan d adalah bagian desimal dari bilangan yang diperoleh rumus pertama.

Sekarang Anda mungkin berpikir bahwa mencari persentil sampel atau populasi statistik itu rumit karena metodenya melibatkan banyak langkah, namun sebenarnya mudah. Bacalah dua contoh konkrit berikut dan saya yakin Anda akan memahaminya dengan lebih baik.

Catatan : Komunitas ilmiah belum sepenuhnya sepakat tentang cara menghitung persentil, jadi Anda dapat menemukan buku statistik yang menjelaskannya sedikit berbeda.

Contoh Perhitungan Persentil

Seperti yang sudah Anda lihat pada penjelasan cara mencari persentil suatu sampel di atas, perhitungannya berbeda-beda tergantung hasil rumus pertama adalah desimal atau bukan. Itu sebabnya di bawah ini Anda akan menemukan dua contoh penyelesaian, satu untuk setiap kasus.

Contoh 1

Dari data pada tabel berikut, hitunglah persentil ke-1, ke-43, dan ke-89.

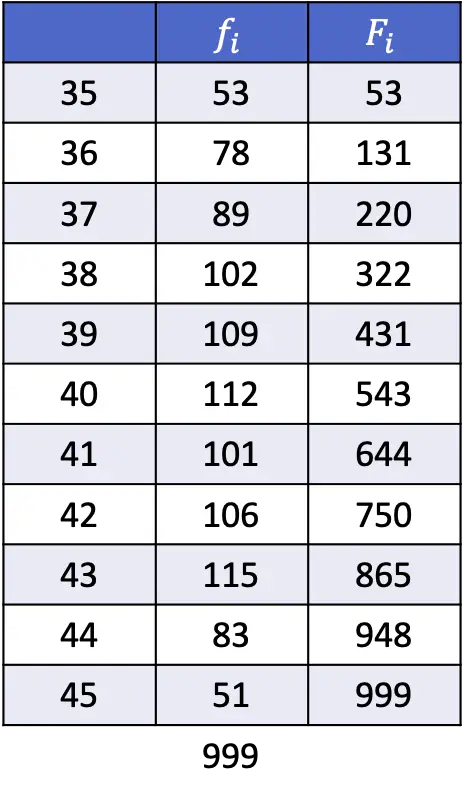
Seperti yang telah dijelaskan pada bagian sebelumnya, rumus mencari posisi persentil adalah:

$\cfrac{k\cdot (n+1)}{100} \qquad k=1, 2, 3,\ldots ,97,98,99$

Dalam hal ini, ukuran sampel untuk latihan ini adalah 999 data statistik, jadi untuk menghitung posisi persentil pertama kita perlu mengganti n dengan 999 dan k dengan 1 :

$\cfrac{1\cdot (999+1)}{100}=10\quad \color{orange}\bm{\longrightarrow}\color{black}\quad P_1=35$

Jadi persentil pertama adalah persentil yang frekuensi absolut kumulatifnya langsung lebih besar dari 10, yang dalam hal ini adalah 35 karena frekuensi absolut kumulatifnya adalah 53.

Untuk menentukan persentil ke-43 harus menggunakan rumus yang sama tetapi yang jelas kali ini k kita ganti dengan 43.

$\cfrac{43\cdot (999+1)}{100}=430\quad \color{orange}\bm{\longrightarrow}\color{black}\quad P_{43}=39$

Frekuensi kumulatif absolut tepat di atas 430 adalah 431 dari data 39, sehingga persentil ke-43 sama dengan 39.

Terakhir, kami menerapkan rumus yang sama untuk mendapatkan persentil ke-89:

$\cfrac{89\cdot (999+1)}{100}=890\quad \color{orange}\bm{\longrightarrow}\color{black}\quad P_{89}=44$

Frekuensi absolut kumulatif dari nilai 44 adalah 948, yang langsung lebih besar dari 890. Oleh karena itu, persentil ke-89 adalah 44.

Contoh 2

Temukan persentil ke-35 dan ke-67 dari rangkaian data berikut:

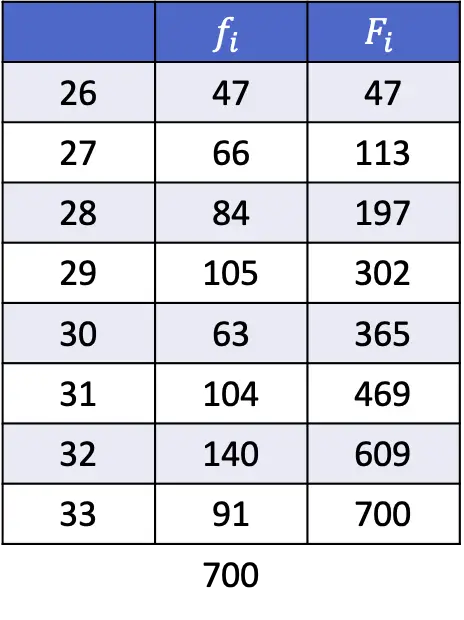
Sekalipun dalam latihan ini kita harus melakukan lebih banyak perhitungan, prinsipnya tetap sama: kita harus menghitung posisi persentil dengan persamaan berikut.

$\cfrac{k\cdot (n+1)}{10} \qquad k=1, 2, 3,\ldots ,97,98,99$

Jadi, untuk menghitung persentil ke-35 kita mengganti k dengan 35 dan n dengan jumlah data, yaitu 700:

$\cfrac{35\cdot (700+1)}{100}=245,35$

Namun kali ini kita mendapatkan angka desimal dari rumusnya, jadi kita perlu menerapkan ekspresi aljabar berikut untuk menghitung nilai persentil yang tepat:

$P=x_i+d\cdot (x_{i+1}-x_i)$

Angka yang diberikan pada rumus pertama adalah 245,35, jadi persentil ke-35 berada di antara posisi 245 dan 246, yang masing-masing sesuai dengan nilai 29 dan 29. Jadi, x _i adalah 29, x _i+1 adalah 29 dan d bernilai desimal dari bilangan yang diperoleh, yaitu 0,35.

$P_{35}=29+0,35\cdot (29-29)=29$

Untuk mencari persentil ke-67, kita perlu menggunakan cara yang sama. Pertama-tama kita hitung posisi persentilnya:

$\cfrac{67\cdot (700+1)}{100}=469,67$

Angka yang dihasilkan 469,67 menunjukkan bahwa persentil akan berada di antara posisi 469 dan 470, yang nilainya 31 dan 32. Oleh karena itu, kami menggunakan rumus kedua dalam proses mencari nilai persentil yang tepat:

$P_{67}=31+0,67\cdot (32-31)=31,67$

kalkulator persentil

Masukkan kumpulan data statistik dan angka persentil yang ingin Anda hitung ke dalam kalkulator berikut. Data harus dipisahkan dengan spasi dan dimasukkan menggunakan titik sebagai pemisah desimal.

Persentil dalam data yang dikelompokkan

Untuk menghitung persentil ketika data dikelompokkan ke dalam kelompok , pertama-tama kita perlu mencari kelompok atau kelas yang termasuk dalam persentil tersebut menggunakan rumus berikut:

$\cfrac{k\cdot (n+1)}{100} \qquad k=1, 2, 3,\ldots ,97,98,99$

Oleh karena itu, persentilnya akan berada dalam interval yang frekuensi absolutnya lebih besar daripada angka yang diperoleh pada persamaan sebelumnya.

Dan setelah kita mengetahui interval persentilnya, kita harus menerapkan rumus berikut untuk mencari nilai pasti persentil tersebut:

$P_k=L_i+\cfrac{\displaystyle\frac{k\cdot (n+1)}{100}-F_{i-1}}{f_i}\cdot I_i \qquad k=1,2,3,\ldots ,97,98,99$

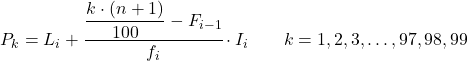
Emas:

L _i adalah batas bawah interval letak persentil.
n adalah jumlah total pengamatan.
F _i-1 adalah frekuensi absolut kumulatif dari interval sebelumnya.
f _i adalah frekuensi absolut dari interval di mana persentil berada.
I _i adalah lebar interval persentil.

Di bawah ini adalah latihan langkah demi langkah tentang cara memperoleh persentil ketika data dinyatakan dalam interval. Secara khusus, persentil ke-29, ke-52, dan ke-98 dihitung.

Data dalam sampel ini dikelompokkan berdasarkan interval, jadi kita perlu melakukan dua langkah untuk menentukan persentil: pertama kita perlu mencari interval di mana persentil berada, lalu menerapkan rumus untuk menghitung nilai persentil yang tepat. persentil.

Jadi, kita mencari posisi persentil ke-29 dengan persamaan berikut:

$\cfrac{k\cdot (n+1)}{100}$

$\cfrac{29\cdot (500+1)}{100} =145,29 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad [350,375)$

Interval persentil adalah interval yang frekuensi absolut kumulatifnya langsung lebih besar dari 145,29, yang dalam hal ini adalah interval [350,375) yang frekuensi absolut kumulatifnya adalah 175. Dan setelah kita mengetahui interval persentilnya, kita terapkan rumus berikut untuk menghitungnya nilai persisnya:

$P_k=L_i+\cfrac{\displaystyle\frac{k\cdot (n+1)}{100}-F_{i-1}}{f_i}\cdot I_i$

$P_{29}=350+\cfrac{\displaystyle\frac{29\cdot (500+1)}{100}-131}{44}\cdot 25=358,12$

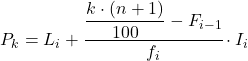
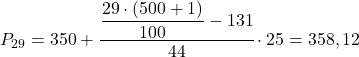
Sekarang kita ulangi prosedur yang sama untuk menghitung persentil ke-52. Pertama-tama kita hitung intervalnya:

$\cfrac{52\cdot (500+1)}{100} =260,52 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad [400,425)$

Interval persentil ke-52 adalah [400.425) karena frekuensi absolut kumulatifnya (298) tepat di atas 260.52. Oleh karena itu, nilai persentil yang sebenarnya adalah:

$P_{52}=400+\cfrac{\displaystyle\frac{52\cdot (500+1)}{100}-234}{64}\cdot 25=410,36$

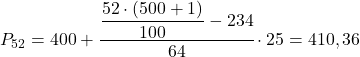
Terakhir, kita akan menemukan persentil ke-98. Seperti biasa, pertama-tama kita menghitung interval letaknya:

$\cfrac{98\cdot (500+1)}{100} =490,98 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad [475,500)$

Dan setelah kita mengetahui interval letak persentilnya, kita menghitung nilai pastinya dengan rumus berikut:

$P_{98}=475+\cfrac{\displaystyle\frac{98\cdot (500+1)}{100}-442}{58}\cdot 25=496,11$

Tentang Penulis

Benjamin anderson

Halo, saya Benjamin, pensiunan profesor statistika yang menjadi guru Statorial yang berdedikasi. Dengan pengalaman dan keahlian yang luas di bidang statistika, saya ingin berbagi ilmu untuk memberdayakan mahasiswa melalui Statorials. Baca selengkapnya

Apa itu persentil?

Cara menghitung persentil

Contoh Perhitungan Persentil

Contoh 1

Contoh 2

kalkulator persentil

Persentil dalam data yang dikelompokkan

Tentang Penulis

Benjamin anderson

Tambahkan komentar