Cara menggunakan tabel z (dengan contoh)
Tabel z adalah tabel yang memberi tahu Anda berapa persentase nilai yang berada di bawah skor z tertentu dalam distribusi normal standar.
Skor-z hanya memberi tahu Anda berapa banyak standar deviasi suatu nilai data individual yang turun dari rata-ratanya. Ini dihitung sebagai berikut:
skor-z = (x – μ) / σ
Emas:
- x: nilai data individu
- μ: rata-rata populasi
- σ: deviasi standar populasi
Tutorial ini menunjukkan beberapa contoh penggunaan tabel z.
Contoh 1
Nilai ujian masuk perguruan tinggi tertentu berdistribusi normal dengan mean μ = 82 dan simpangan baku σ = 8. Kira-kira berapa persentase siswa yang mendapat nilai ujian di bawah 84?
Langkah 1: Temukan skor-z.
Pertama, kita akan menemukan skor-z yang terkait dengan skor ujian 84:
skor-z = (x – μ) / σ = (84 – 82) / 8 = 2/8 = 0,25
Langkah 2: Gunakan grafik z untuk menemukan persentase yang sesuai dengan skor z.
Selanjutnya kita akan mencari nilai 0,25 pada tabel z:

Sekitar 59,87% siswa mendapat nilai di bawah 84 dalam ujian ini.
Contoh 2
Tinggi tanaman pada suatu taman berdistribusi normal dengan rata-rata μ = 26,5 inci dan simpangan baku σ = 2,5 inci. Kira-kira berapa persentase tanaman yang tingginya lebih dari 26 inci?
Langkah 1: Temukan skor-z.
Pertama, kita akan menemukan skor-z yang terkait dengan tinggi 26 inci.
skor-z = (x – μ) / σ = (26 – 26,5) / 2,5 = -0,5 / 2,5 = -0,2
Langkah 2: Gunakan grafik z untuk menemukan persentase yang sesuai dengan skor z.
Selanjutnya kita akan mencari nilai -0.2 di tabel z:
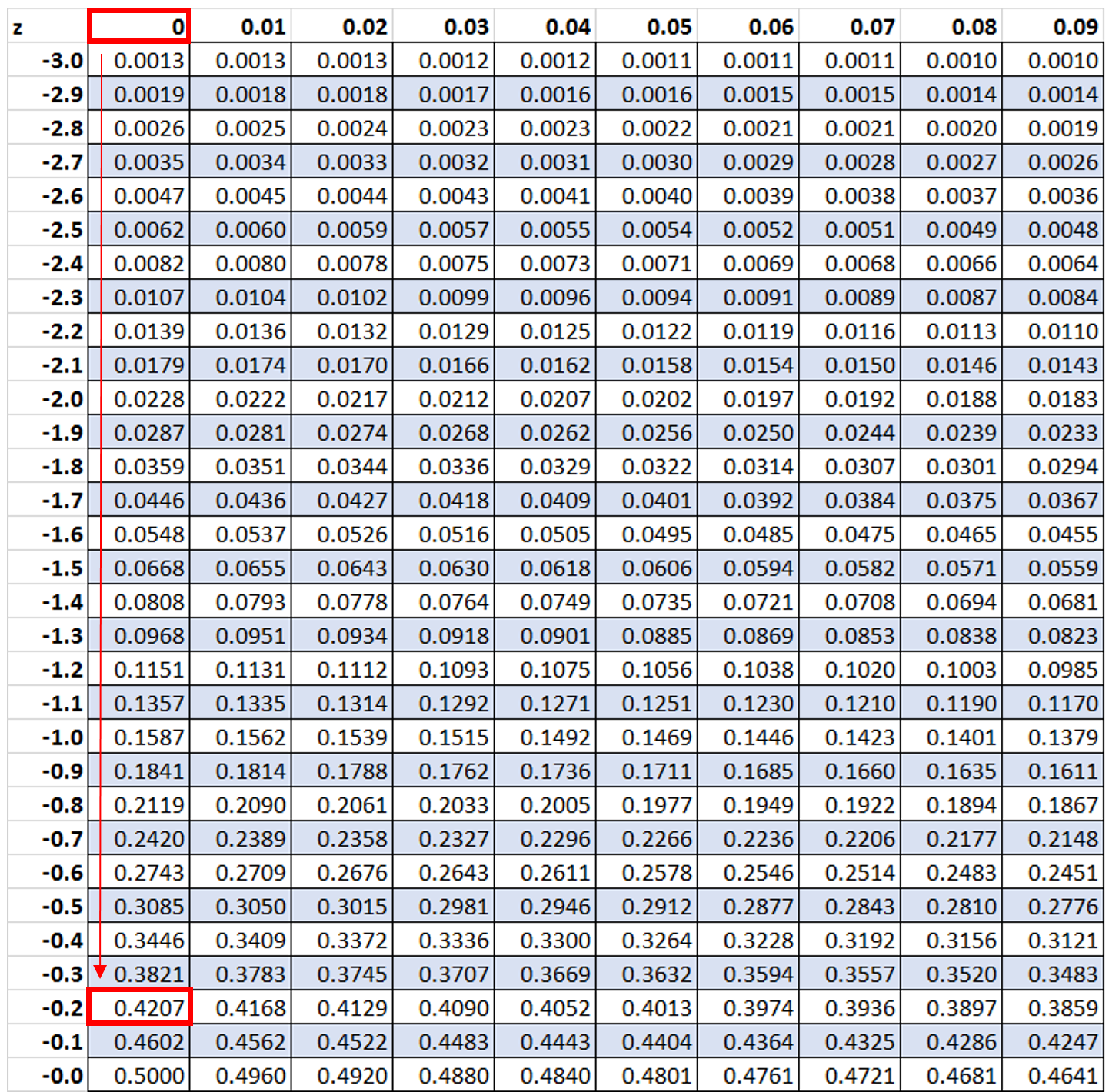
Kami melihat 42,07% nilainya berada di bawah skor z -0,2. Namun pada contoh ini kita ingin mengetahui berapa persentase nilai yang lebih besar dari -0.2, yang dapat kita cari dengan menggunakan rumus 100% – 42.07% = 57.93%.
Jadi, sekitar 59,87% tanaman di taman ini tingginya lebih dari 26 inci.
Contoh 3
Berat spesies lumba-lumba tertentu berdistribusi normal dengan rata-rata μ = 400 pon dan simpangan baku σ = 25 pon. Kira-kira berapa persentase lumba-lumba yang memiliki berat antara 410 dan 425 pon?
Langkah 1: Temukan skor-z.
Pertama, kita akan menemukan skor-z yang terkait dengan 410 buku dan 425 buku
z-skor 410 = (x – μ) / σ = (410 – 400) / 25 = 10/25 = 0,4
z skor 425 = (x – μ) / σ = (425 – 400) / 25 = 25 / 25 = 1
Langkah 2: Gunakan bagan z untuk menemukan persentase yang sesuai dengan setiap skor z.
Pertama, kita akan mencari nilai 0,4 di tabel z:

Selanjutnya kita akan mencari nilai 1 di tabel z:

Terakhir, kita akan mengurangkan nilai terkecil dari nilai terbesar: 0.8413 – 0.6554 = 0.1859 .
Jadi, sekitar 18,59% lumba-lumba memiliki berat antara 410 dan 425 pon.
Sumber daya tambahan
Pengenalan distribusi normal
Kalkulator Area Distribusi Normal
Kalkulator skor Z