Uji eksak fisher: definisi, rumus dan contoh
Uji eksak Fisher digunakan untuk mengetahui ada atau tidaknya hubungan yang signifikan antara dua variabel kategori. Biasanya digunakan sebagai alternatif uji independensi chi-kuadrat ketika satu atau lebih jumlah sel dalam tabel 2 × 2 kurang dari 5.
Uji eksak Fisher menggunakan hipotesis nol dan hipotesis alternatif berikut:
- H 0 : (hipotesis nol) Kedua variabel tersebut independen.
- H 1 : (hipotesis alternatif) Kedua variabel tersebut tidak independen.
Misalkan kita memiliki tabel 2×2 berikut:
| Grup 1 | Grup 2 | Jumlah baris | |
| Kategori 1 | MEMILIKI | B | a+b |
| Kategori 2 | vs. | D | c+d |
| Kolom jumlah | a+c | b+d | a+b+c+d = n |
Nilai p satu sisi untuk uji eksak Fisher dihitung sebagai berikut:
p = (a+b)!(c+d)!(a+c)!(b+d)! / (a!b!c!d!n!)
Ini menghasilkan nilai p yang sama dengan CDF distribusi hipergeometri dengan parameter berikut:
- ukuran populasi = n
- “keberhasilan” populasi = a+b
- ukuran sampel = a + c
- contoh “sukses” = satu
Nilai p dua sisi untuk uji eksak Fisher kurang mudah dihitung dan tidak dapat diperoleh hanya dengan mengalikan nilai p satu sisi dengan dua. Untuk mencari nilai p dua sisi, sebaiknya gunakan kalkulator uji eksak Fisher .
Tes eksak Fisher: contoh
Misalkan kita ingin mengetahui apakah gender dikaitkan dengan preferensi terhadap suatu partai politik atau tidak. Kami mengambil sampel acak sederhana dari 25 pemilih dan menanyakan preferensi partai politik mereka. Berikut tabel hasil surveinya:
| Demokrat | Republik | Total | |
| Pria | 4 | 9 | 13 |
| Perempuan | 8 | 4 | 12 |
| Total | 12 | 13 | 25 |
Langkah 1: Tentukan asumsi.
Kami akan melakukan uji eksak Fisher menggunakan asumsi berikut:
- H 0 : Preferensi gender dan partai politik bersifat independen.
- H 1 : Preferensi gender dan partai politik tidak independen.
Langkah 2: Perhitungan nilai p dua sisi.
Kita dapat menggunakan kalkulator uji eksak Fisher dengan masukan berikut:
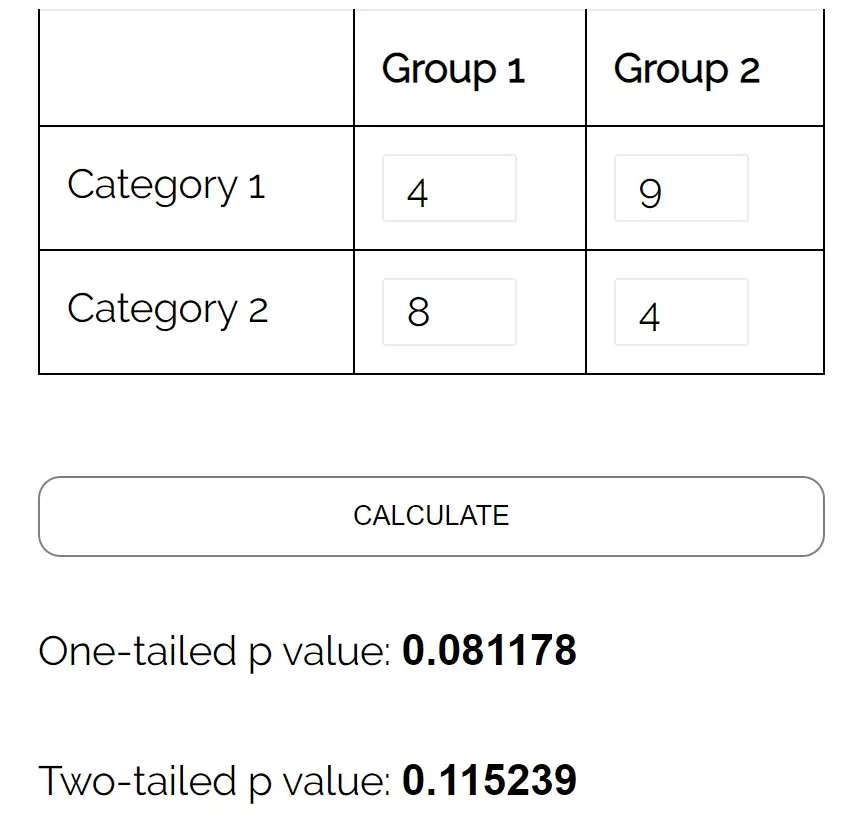
Nilai p dua sisi adalah 0,115239 . Nilai ini kurang dari 0,05, kami tidak dapat menolak hipotesis nol. Kami tidak memiliki cukup bukti untuk mengatakan bahwa terdapat hubungan yang signifikan secara statistik antara gender dan preferensi terhadap partai politik.
Sumber daya tambahan
Tutorial berikut menjelaskan cara melakukan uji eksak Fisher menggunakan program statistik yang berbeda:
Bagaimana melakukan uji eksak Fisher di R
Bagaimana Melakukan Tes Tepat Fisher di Excel
Cara melakukan tes eksak Fisher di Stata
Cara Melakukan Tes Eksak Fisher di SPSS
Cara Melakukan Tes Tepat Fisher dengan Python
Kalkulator Tes Tepat Fisher