Perbedaan sedang

Oleh Benjamin anderson Agustus 5, 2023 Statistik 0 Komentar

Artikel ini menjelaskan apa itu deviasi rata-rata dan cara menghitungnya. Anda juga akan menemukan contoh nyata dalam menghitung deviasi rata-rata. Dan, terlebih lagi, Anda akan dapat menghitung deviasi rata-rata dari setiap kumpulan data statistik menggunakan kalkulator online.

Apa yang dimaksud dengan deviasi rata-rata?

Deviasi rata-rata , juga disebut deviasi absolut rata-rata , adalah ukuran dispersi statistik.

Deviasi rata-rata suatu kumpulan data adalah rata-rata deviasi absolut . Oleh karena itu, simpangan rata-rata sama dengan jumlah simpangan setiap item data dari rata-rata aritmatika dibagi dengan jumlah item data.

Dengan kata lain rumus simpangan rata-rata adalah sebagai berikut:

👉 Anda dapat menggunakan kalkulator di bawah ini untuk menghitung deviasi rata-rata dari kumpulan data apa pun.

Dalam statistika, simpangan rata-rata disebut juga simpangan absolut rata-rata .

Penafsiran simpangan rata-rata dilakukan sebagai berikut: semakin besar nilai simpangan rata-rata, berarti data tersebut rata-rata semakin jauh dari rata-rata aritmatika; sebaliknya semakin rendah rata-rata deviasi maka semakin dekat nilainya. datanya adalah. Oleh karena itu, simpangan rata-rata menunjukkan sebaran suatu rangkaian data.

Ukuran lain yang dianggap terdistribusi adalah jangkauan, jangkauan antarkuartil, deviasi standar (atau deviasi standar), varians, dan koefisien variasi.

Cara menghitung rata-rata deviasi

Untuk menghitung deviasi rata-rata suatu rangkaian data, langkah-langkah berikut harus diikuti:

Hitung mean aritmatika dari kumpulan data statistik.
Hitung deviasi setiap titik data dari mean, yang didefinisikan sebagai nilai absolut selisih antara data dan mean.
Jumlahkan semua selisih yang dihitung pada langkah sebelumnya.
Bagilah dengan jumlah total data. Hasil yang diperoleh adalah rata-rata deviasi dari rangkaian data tersebut.

Ringkasnya, rumus yang harus diterapkan untuk mencari rata-rata simpangan adalah:

$D_{\overline{x}}=\cfrac{\sum_{i=1}^N|x_i-\overline{x}|}{N}$

Contoh penghitungan rata-rata deviasi

Mempertimbangkan definisi deviasi rata-rata, di bawah ini adalah contoh penyelesaian langkah demi langkah dalam menghitung deviasi rata-rata sampel statistik. Dengan cara ini Anda akan lebih memahami cara mendapatkan rata-rata deviasi.

Seorang analis mempelajari hasil ekonomi suatu perusahaan selama setahun terakhir dan mempunyai informasi tentang laba yang diperoleh perusahaan selama setiap kuartal tahun tersebut: 2, 3, 7 dan 5 juta dolar. Berapa rata-rata deviasi datanya?

Pertama, kita perlu menghitung rata-rata datanya, lalu kita jumlahkan dan bagi dengan jumlah total observasi (4):

$\overline{x}=\cfrac{2+3+7+5}{4}=4,25$

Setelah kita menghitung mean aritmatika, kita menggunakan rumus deviasi mean:

$D_{\overline{x}}=\cfrac{\sum_{i=1}^N|x_i-\overline{x}|}{N}$

Kami mengganti data ke dalam rumus:

$D_{\overline{x}}=\cfrac{|2-4,25|+|3-4,25|+|7-4,25|+|5-4,25|}{4}$

Kami melakukan perhitungan di pembilang:

$D_{\overline{x}}=\cfrac{|-2,25|+|-1,25|+|2,75|+|0,75|}{4}$

$D_{\overline{x}}=\cfrac{2,25+1,25+2,75+0,75}{4}$

$D_{\overline{x}}=\cfrac{7}{4}$

Dan terakhir, kita bagi dengan jumlah total data untuk mendapatkan rata-rata deviasi sampel:

$D_{\overline{x}}=1,75$

Kalkulator Deviasi Rata-rata

Masukkan sekumpulan data statistik ke dalam kalkulator berikut untuk menghitung deviasi rata-ratanya. Data harus dipisahkan dengan spasi dan dimasukkan menggunakan titik sebagai pemisah desimal.

Deviasi rata-rata untuk data yang dikelompokkan

Untuk menghitung simpangan rata-rata data yang dikelompokkan ke dalam interval, langkah-langkah berikut harus diikuti:

Tentukan mean aritmatika dari kumpulan data statistik. Karena datanya dikelompokkan, ekspresi untuk menghitung rata-ratanya adalah:

$\overline{x}=\cfrac{\sum_{i=1}^N x_i\cdot f_i}{N}$

Hitung simpangan setiap interval dari mean, yang setara dengan nilai absolut selisih antara nilai kelas dan mean.

$|x_i-\overline{x}|$

Kalikan deviasi setiap interval dengan frekuensi absolutnya.

$|x_i-\overline{x}|\cdot f_i$

Jumlahkan semua hasil langkah sebelumnya, lalu bagi dengan jumlah data seluruhnya. Hasil yang diperoleh adalah rata-rata simpangan sampel yang dikelompokkan ke dalam interval-interval.

$\cfrac{\sum_{i=1}^N|x_i-\overline{x}|\cdot f_i}{N}$

Kesimpulannya, rumus untuk memperoleh rata-rata deviasi dari data yang dikelompokkan adalah:

$D_{\overline{x}}=\cfrac{\sum_{i=1}^N|x_i-\overline{x}|\cdot f_i}{N}$

Ketika data dikelompokkan, biasanya berarti terdapat banyak data dan menemukan deviasi rata-rata memerlukan banyak langkah. Oleh karena itu, tabel frekuensi biasanya digunakan untuk melakukan perhitungan.

Di bawah ini adalah latihan langkah demi langkah tentang cara menghitung deviasi rata-rata ketika data dikelompokkan ke dalam interval:

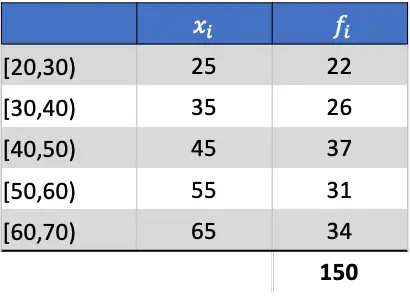
Hal pertama yang dilakukan adalah menghitung rata-rata data yang dikelompokkan. Untuk melakukan ini, kita menambahkan kolom ke tabel dengan mengalikan catatan kelas dengan frekuensinya:

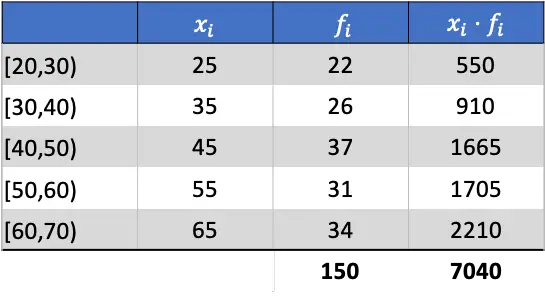
Oleh karena itu, mean aritmatika adalah hasil pembagian jumlah kolom yang ditambahkan dengan jumlah frekuensi absolut:

$\overline{x}=\cfrac{\sum_{i=1}^N x_i\cdot f_i}{N}=\cfrac{7040}{150}=46,93$

Sekarang setelah kita mengetahui rata-rata datanya, kita dapat menambahkan semua kolom yang diperlukan untuk mencari deviasi rata-rata:

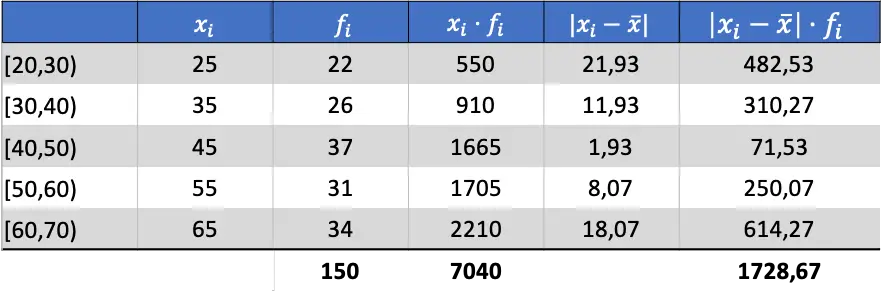
Jadi, untuk mendapatkan simpangan rata-rata Anda harus membagi jumlah kolom terakhir dengan jumlah observasi:

$D_{\overline{x}}=\cfrac{\sum_{i=1}^N|x_i-\overline{x}|\cdot f_i}{N}=\cfrac{1728,67}{150}=11,52$

Tentang Penulis

Benjamin anderson

Halo, saya Benjamin, pensiunan profesor statistika yang menjadi guru Statorial yang berdedikasi. Dengan pengalaman dan keahlian yang luas di bidang statistika, saya ingin berbagi ilmu untuk memberdayakan mahasiswa melalui Statorials. Baca selengkapnya