Pengantar distribusi geometri

Distribusi geometri menggambarkan kemungkinan mengalami sejumlah kegagalan tertentu sebelum mengalami keberhasilan pertama dalam serangkaian percobaan Bernoulli.

Uji coba Bernoulli adalah eksperimen yang hanya memiliki dua kemungkinan hasil – “berhasil” atau “gagal” – dan probabilitas keberhasilannya sama setiap kali eksperimen dilakukan.

Contoh esai Bernoulli adalah lemparan koin. Koin hanya dapat mendarat pada dua kepala (kita mungkin menyebut kepala sebagai “pukulan” dan ekor sebagai “gagal”) dan probabilitas keberhasilan pada setiap pelemparan adalah 0,5, dengan asumsi koin tersebut adil.

Jika suatu variabel acak X mengikuti distribusi geometri, maka peluang mengalami k kegagalan sebelum mengalami keberhasilan pertama dapat dicari dengan rumus berikut:

P(X=k) = (1-p) ^kp

Emas:

• k : jumlah kegagalan sebelum kesuksesan pertama
• p : probabilitas keberhasilan pada setiap percobaan

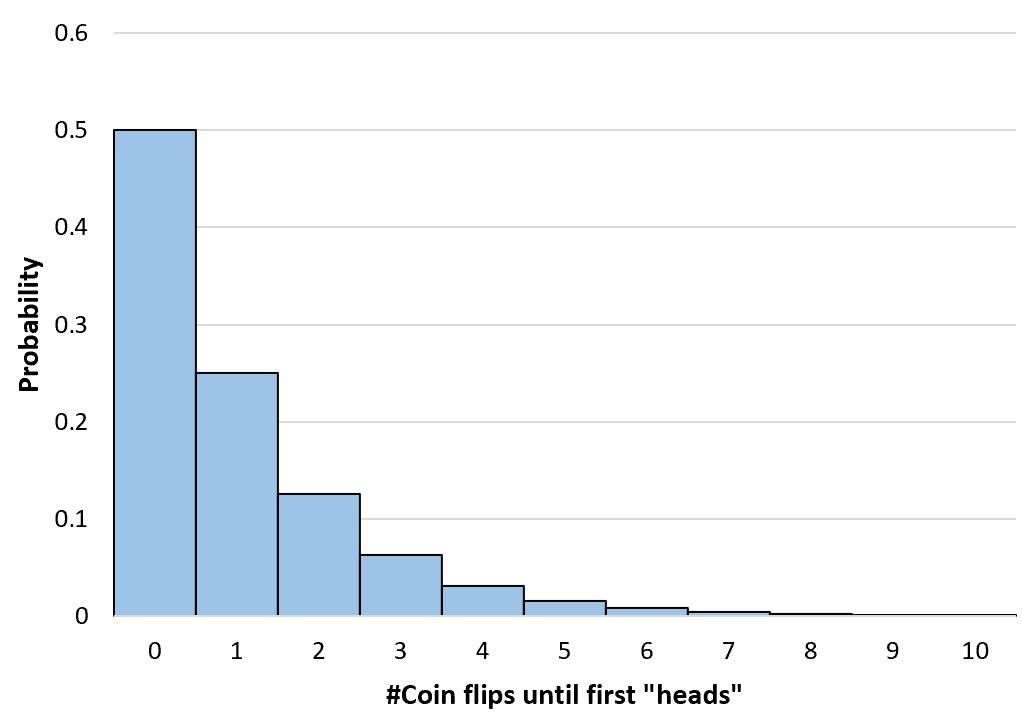
Sebagai contoh, katakanlah kita ingin mengetahui berapa kali kita harus melempar sebuah koin hingga muncul kepala. Kita dapat menggunakan rumus di atas untuk menentukan peluang mengalami kegagalan 0, 1, 2, 3, dst. sebelum koin mendarat di kepala:

Catatan: koin dapat mengalami 0 “kegagalan” jika muncul gambar pada pelemparan pertama.

P(X=0) = (1-.5) ⁰ (.5) = 0.5

P(X=1) = (1-.5) ¹ (.5) = 0.25

P(X=2) = (1-.5) ² (.5) = 0.125

P(X=3) = (1-0,5) ³ (0,5) = 0,0625

Kita dapat menghitung peluang pelemparan koin sebanyak berapa pun hingga tak terhingga. Kami kemudian membuat histogram sederhana untuk memvisualisasikan distribusi probabilitas ini:

Perhitungan probabilitas geometri kumulatif

Probabilitas kumulatif kita mengalami k atau lebih sedikit kegagalan hingga keberhasilan pertama dapat dicari dengan rumus berikut:

P(X≤k) = 1 – (1-p) ^k+1

Emas:

• k : jumlah kegagalan sebelum kesuksesan pertama
• p : probabilitas keberhasilan pada setiap percobaan

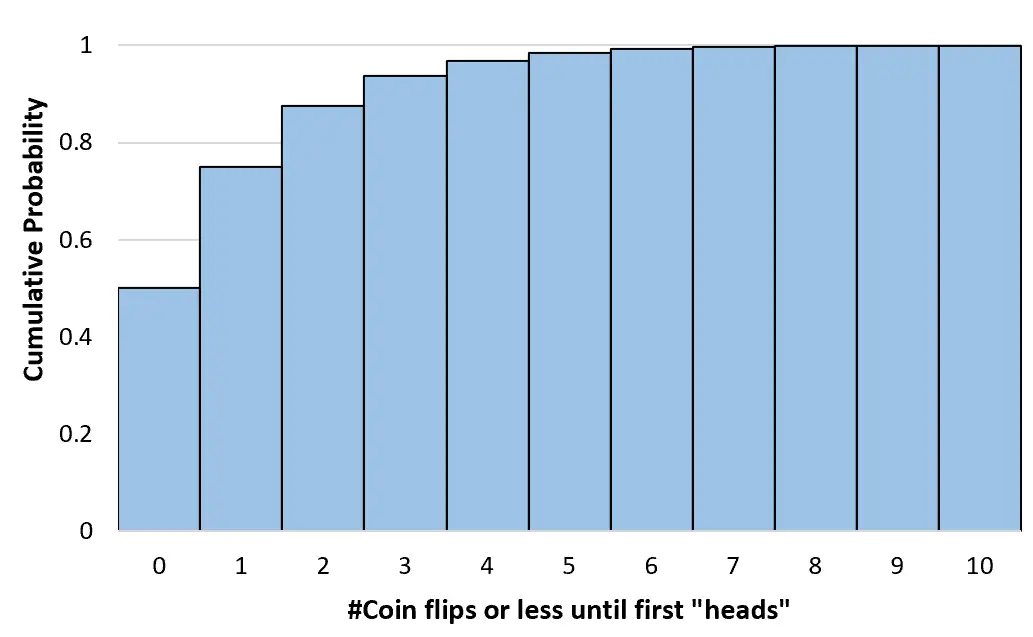
Misalnya, kita ingin mengetahui probabilitas bahwa diperlukan tiga kali atau lebih “kesalahan” sebelum koin akhirnya mendarat di kepala. Kami akan menggunakan rumus berikut untuk menghitung probabilitas ini:

P(X≤3) = 1 – (1-0,5) ³⁺¹ = 0,9375

Kita dapat menghitung setiap probabilitas kumulatif menggunakan rumus serupa:

P(X≤0) = 1 – (1-.5) ⁰⁺¹ = 0.5

P(X≤1) = 1 – (1-0,5) ¹⁺¹ = 0,75

P(X≤2) = 1 – (1-0,5) ²⁺¹ = 0,875

Kita dapat menghitung probabilitas kumulatif ini untuk sejumlah pelemparan koin hingga tak terhingga. Kita kemudian dapat membuat histogram untuk memvisualisasikan distribusi probabilitas kumulatif ini:

Sifat-sifat distribusi geometri

Distribusi geometri mempunyai sifat-sifat sebagai berikut:

Rata-rata distribusinya adalah (1-p) / p .

Varians distribusinya adalah (1-p) / p ² .

Misalnya:

Frekuensi rata-rata yang kita harapkan sebuah koin mendaratkan kepala sebelum mendaratkan ekornya adalah (1-p) / p = (1-.5) / .5 = 1 .

Varians banyaknya pelemparan hingga mengenai kepala adalah (1-p)/ ^p2 =(1-.5)/. ⁵² = 2 .

Soal Praktek Distribusi Geometri

Gunakan soal latihan berikut untuk menguji pengetahuan Anda tentang distribusi geometri.

Catatan: Kami akan menggunakan Kalkulator Distribusi Geometris untuk menghitung jawaban atas pertanyaan-pertanyaan ini.

Masalah 1

Pertanyaan: Seorang peneliti menunggu di luar perpustakaan untuk menanyakan orang-orang apakah mereka mendukung undang-undang tertentu. Peluang seseorang mendukung hukum adalah p = 0,2. Berapa probabilitas bahwa orang keempat yang diajak bicara oleh peneliti akan menjadi orang pertama yang mendukung undang-undang tersebut?

Jawaban: Banyaknya “kegagalan” sampai keberhasilan pertama – yaitu banyaknya orang yang tidak mendukung hukum sampai orang pertama mendukungnya – adalah 3. Jadi, dalam menggunakan kalkulator distribusi geometri dengan p = 0,2 dan x = 3 kegagalan, kita temukan bahwa P(X=3) = 0.10240 .

Masalah 2

Pertanyaan: Seorang peneliti menunggu di luar perpustakaan untuk menanyakan orang-orang apakah mereka mendukung undang-undang tertentu. Peluang seseorang mendukung hukum adalah p = 0,2. Berapa probabilitas peneliti harus berbicara dengan lebih dari empat orang untuk menemukan seseorang yang mendukung undang-undang tersebut?

Jawaban: Dengan menggunakan kalkulator distribusi geometri dengan kegagalan p =0,2 dan x = 4, kita menemukan bahwa P(X>4) = 0,32768 .

Masalah 3

Pertanyaan: Seorang peneliti menunggu di luar perpustakaan untuk menanyakan orang-orang apakah mereka mendukung undang-undang tertentu. Peluang seseorang mendukung hukum adalah p = 0,2. Berapa perkiraan jumlah orang yang perlu diajak bicara oleh peneliti sampai dia menemukan seseorang yang mendukung undang-undang tersebut?

Jawaban: Ingatlah bahwa mean dari distribusi geometri adalah (1-p) / p . Dalam situasi ini, rata-ratanya adalah (1-.2) / .2 = 4 .