Pengantar distribusi multinomial

Distribusi multinomial menggambarkan probabilitas diperolehnya sejumlah penghitungan tertentu untuk k hasil yang berbeda, ketika setiap hasil memiliki probabilitas terjadinya yang tetap.

_{Jika suatu} variabel acak _{_} dapat dicari dengan rumus berikut:

Probabilitas = n! * (p ₁ ^{x ₁} * p ₂ ^{x ₂} * … * p _k ^{x _k} ) / (x ₁ ! * x ₂ ! … * x _k !)

Emas:

• n: jumlah total kejadian
• x ₁ : berapa kali hasil 1 muncul
• p ₁ : peluang munculnya hasil 1 pada suatu percobaan tertentu

Misalnya ada 5 kelereng merah, 3 kelereng hijau, dan 2 kelereng biru dalam sebuah guci. Jika kita mengambil 5 kelereng secara acak dari dalam guci, dengan pengembalian, berapa peluang terambil tepat 2 kelereng merah, 2 kelereng hijau, dan 1 kelereng biru?

Untuk menjawab pertanyaan tersebut, kita dapat menggunakan distribusi multinomial dengan parameter sebagai berikut:

• n : 5
• x ₁ (# kelereng merah) = 2, x ₂ (# kelereng hijau) = 2, x ₃ (# kelereng biru) = 1
• p ₁ (masalah merah) = 0,5, p ₂ (masalah hijau) = 0,3, p ₃ (masalah biru) = 0,2

Memasukkan angka-angka ini ke dalam rumus, kita menemukan bahwa probabilitasnya adalah:

Kemungkinan = 5! * (.5 ² * .3 ² * .2 ¹ ) / (2! * 2! * 1!) = 0,135 .

Soal Praktek Distribusi Multinomial

Gunakan soal latihan berikut untuk menguji pengetahuan Anda tentang distribusi multinomial.

Catatan: Kami akan menggunakan Kalkulator Distribusi Multinomial untuk menghitung jawaban atas pertanyaan-pertanyaan ini.

Masalah 1

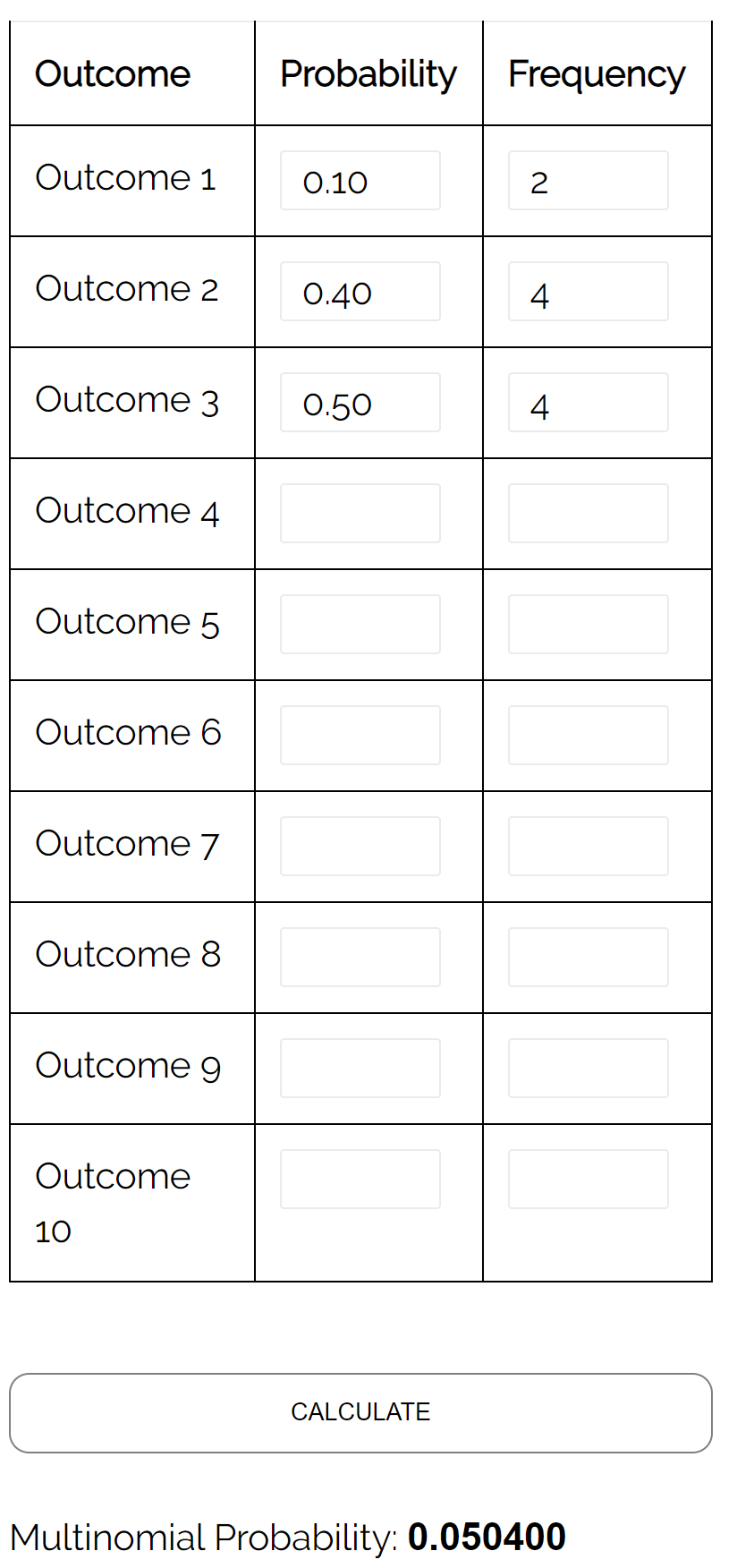
Pertanyaan: Dalam pemilihan walikota tiga arah, calon A memperoleh 10% suara, calon B memperoleh 40% suara, dan calon C memperoleh 50% suara. Jika kita mengambil sampel acak yang terdiri dari 10 pemilih, berapa peluang terambilnya 2 orang memilih calon A, 4 orang memilih calon B, dan 4 orang memilih calon C?

Jawaban: Menggunakan Kalkulator Distribusi Multinomial dengan input berikut, kita menemukan probabilitasnya adalah 0,0504:

Masalah 2

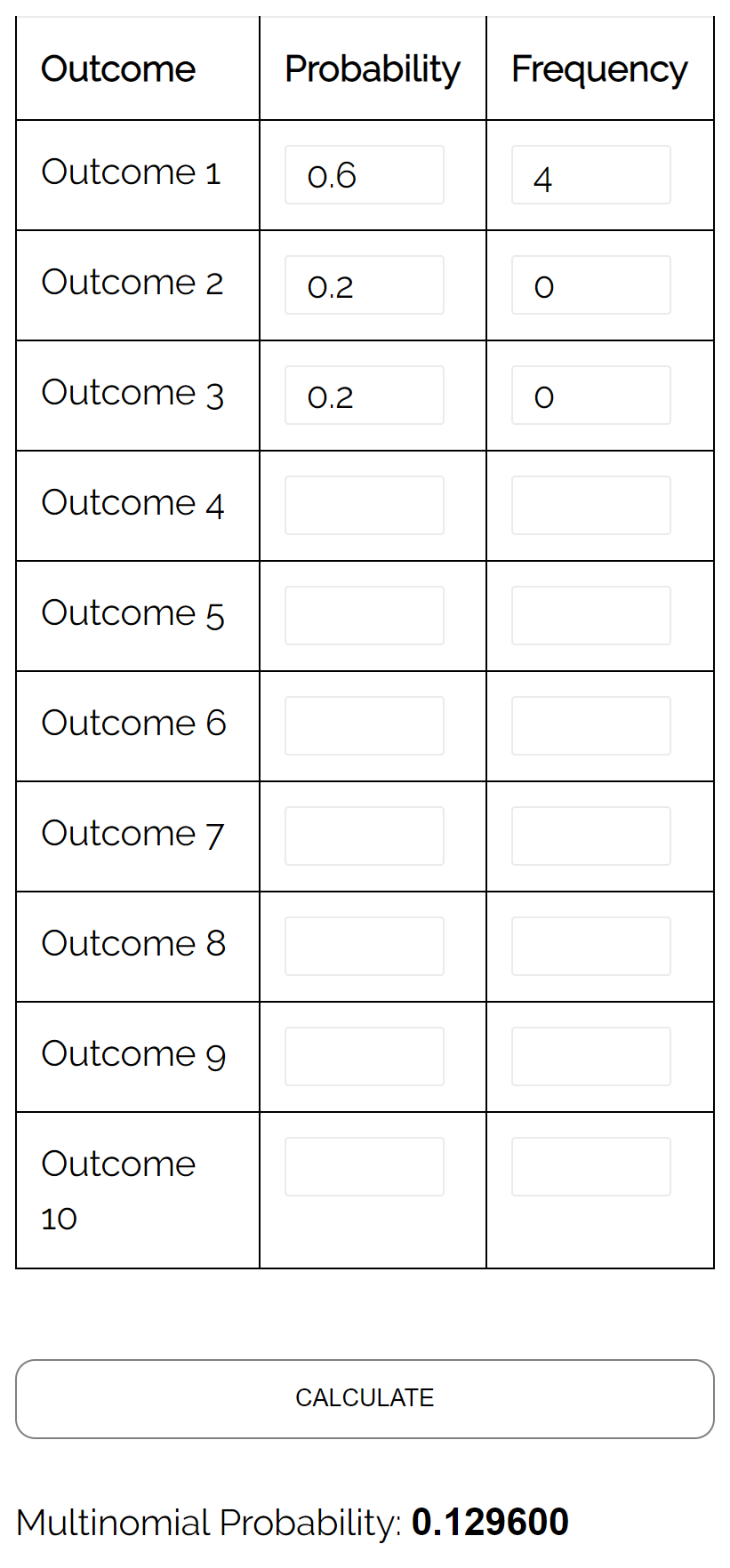
Pertanyaan: Misalkan sebuah guci berisi 6 kelereng kuning, 2 kelereng merah, dan 2 kelereng merah muda. Jika kita mengambil 4 bola secara acak dari dalam guci, dengan pengembalian, berapa peluang terambilnya keempat bola tersebut berwarna kuning?

Jawaban: Menggunakan Kalkulator Distribusi Multinomial dengan input berikut, kita menemukan probabilitasnya adalah 0,1296:

Masalah 3

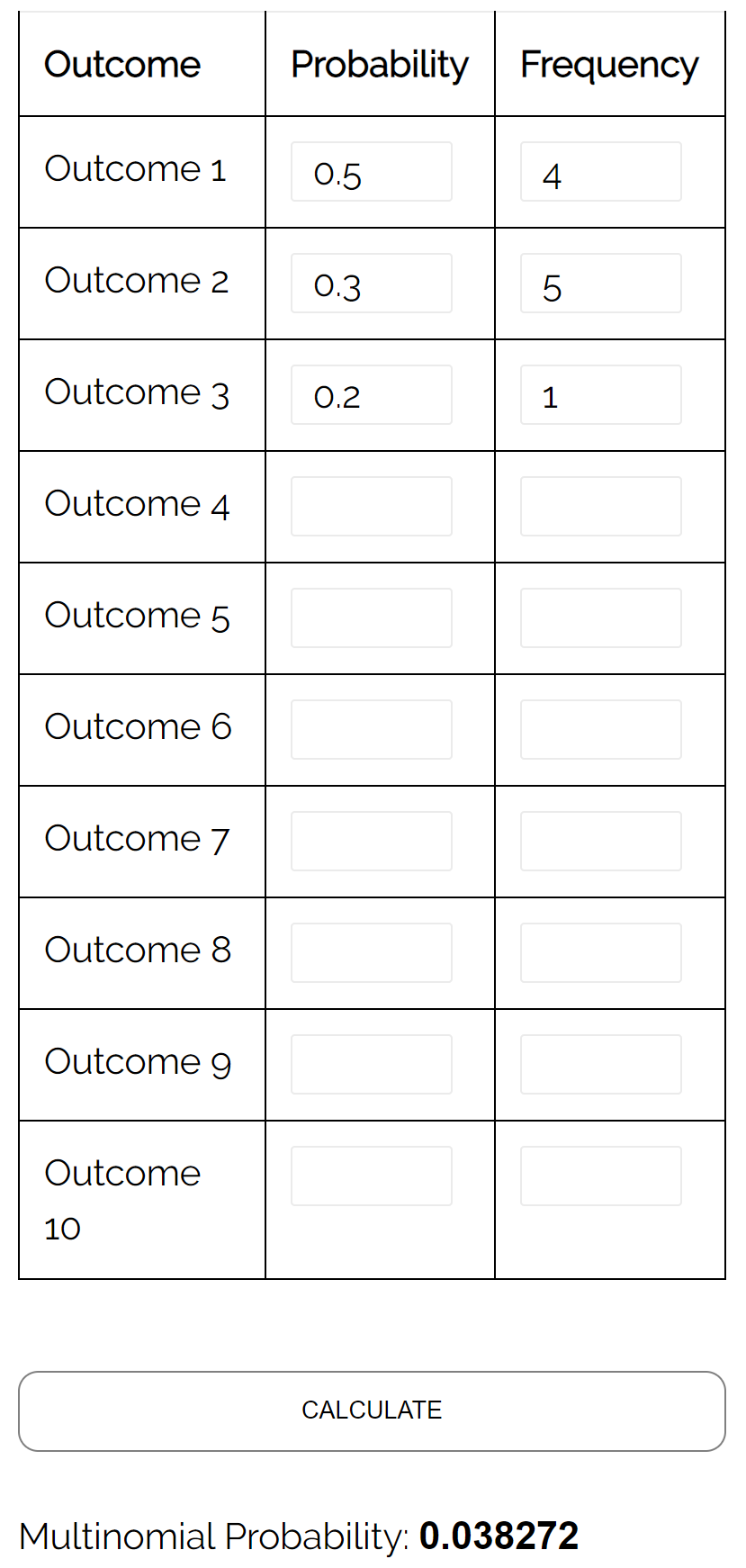
Pertanyaan: Misalkan dua siswa sedang bermain catur melawan satu sama lain. Peluang siswa A memenangkan suatu permainan adalah 0,5, peluang siswa B memenangkan permainan tertentu adalah 0,3, dan peluang terjadinya seri dalam suatu permainan adalah 0, 2. Jika mereka memainkan 10 permainan, berapakah peluang pemain A menang 4 kali, pemain B menang 5 kali, dan seri 1 kali?

Jawaban: Menggunakan Kalkulator Distribusi Multinomial dengan input berikut, kita menemukan probabilitasnya adalah 0,038272:

Sumber daya tambahan

Tutorial berikut memberikan pengenalan distribusi umum lainnya dalam statistik:

Pengenalan distribusi normal
Pengenalan distribusi binomial
Pengenalan distribusi Poisson
Pengantar distribusi geometri