Cara melakukan anova pengukuran berulang secara manual
ANOVA pengukuran berulang digunakan untuk menentukan apakah terdapat perbedaan yang signifikan secara statistik antara rata-rata tiga kelompok atau lebih di mana subjek yang sama muncul di setiap kelompok.
Tutorial ini menjelaskan cara melakukan ANOVA pengukuran berulang satu arah secara manual.
Contoh: Pengukuran ANOVA berulang satu arah dengan tangan
Peneliti ingin mengetahui apakah tiga obat berbeda menyebabkan waktu reaksi berbeda. Untuk mengujinya, mereka mengukur waktu reaksi (dalam detik) lima pasien terhadap setiap obat. Hasilnya ditunjukkan di bawah ini:
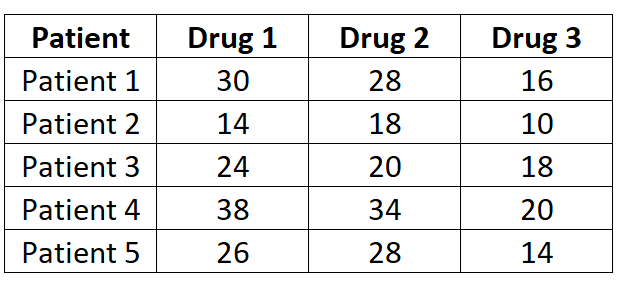
Karena setiap pasien diukur pada masing-masing dari tiga obat, kami akan menggunakan ANOVA pengukuran berulang satu arah untuk menentukan apakah waktu reaksi rata-rata berbeda antar obat.
Ikuti langkah-langkah berikut untuk melakukan pengukuran berulang ANOVA secara manual:
Langkah 1: Hitung SST.
Pertama, kita akan menghitung jumlah total kuadrat (SST), yang dapat dicari dengan menggunakan rumus berikut:
SST = s 2 jumlah (n jumlah -1)
Emas:
- s 2 total : varians untuk kumpulan data
- n total : jumlah total observasi dalam dataset
Pada contoh ini kita menghitung SST sebagai berikut: (64.2667)(15-1) = 899.7
Langkah 2: Hitung SSB
Selanjutnya kita akan menghitung jumlah kuadrat (SSB) yang dapat dicari dengan menggunakan rumus berikut:
SSB = Σn j ( x j – x jumlah ) 2
Emas:
- Σ : simbol Yunani yang berarti “jumlah”
- n j : jumlah observasi pada kelompok ke -j
- x j : rata-rata kelompok ke-j
- x total : rata-rata seluruh data
Pada contoh ini, kita menghitung SSB sebagai berikut: (5)(26.4-22.533) 2 +(5)(25.6-22.533) 2 + (5)(15.6-22.533) 2 = 362.1
Langkah 3: Hitung SSS.
Selanjutnya kita akan menghitung jumlah subjek kuadrat (SSS), yang dapat dicari dengan menggunakan rumus berikut:
SSS =(Σr 2 k /c) – (N 2 /rc)
Emas:
- Σ : simbol Yunani yang berarti “jumlah”
- r 2 k : jumlah kuadrat pasien ke-k
- N : total keseluruhan seluruh data
- r: jumlah total pasien
- c: jumlah total kelompok
Dalam contoh ini, kita menghitung SSS sebagai berikut: ((74 2 + 42 2 + 62 2 + 92 2 + 68 2 )/3) – (338 2 /(5)(3)) = 441.1
Langkah 4: Hitung SES.
Selanjutnya kita akan menghitung jumlah error kuadrat (SSE) yang dapat dicari dengan menggunakan rumus berikut:
SSE = SST – SSB – SSS
Pada contoh ini, kita menghitung SES sebagai berikut: 899.7 – 362.1 – 441.1 = 96.5
Langkah 5: Lengkapi tabel ANOVA pengukuran berulang.
Sekarang kita memiliki SSB, SSS, dan SSE, kita dapat mengisi tabel ANOVA pengukuran berulang:
| Sumber | Jumlah kuadrat (SS) | df | Kuadrat rata-rata (MS) | F |
|---|---|---|---|---|
| Di antara | 362.1 | 2 | 181.1 | 15.006 |
| Subjek | 441.1 | 4 | 110.3 | |
| Kesalahan | 96,5 | 8 | 12.1 |
Inilah cara kami menghitung angka-angka berbeda dalam tabel:
- df antara: #grup – 1 = 3 – 1 = 2
- df subjek: #peserta – 1 = 5 – 1 = 4
- Kesalahan df: df antara * df subjek = 2*4 = 8
- MS masuk : SSB / df masuk = 362.1 / 2 = 181.1
- Mata pelajaran MS : SSS mata pelajaran / df = 441.1 / 4 = 110.3
- Kesalahan MS: Kesalahan SSE / df = 96,5 / 8 = 12.1
- F : MS masuk / MS error = 181.1 / 12.1 = 15.006
Langkah 6: Interpretasikan hasilnya.
Statistik uji F untuk ANOVA pengukuran berulang satu arah ini adalah 15,006 . Untuk menentukan apakah hasil ini signifikan secara statistik, kita perlu membandingkannya dengan nilai kritis F yang terdapat pada tabel distribusi F dengan nilai berikut:
- α (tingkat signifikansi) = 0,05
- DF1 (derajat kebebasan pembilangnya) = df antara = 2
- DF2 (derajat kebebasan penyebut) = error df = 8
Kami menemukan bahwa nilai kritis F adalah 4,459 .
Karena statistik uji F pada tabel ANOVA lebih besar dari nilai kritis F pada tabel distribusi F, maka hipotesis nol kami tolak. Ini berarti bahwa kita mempunyai cukup bukti untuk mengatakan bahwa terdapat perbedaan yang signifikan secara statistik antara waktu respons rata-rata obat-obatan.