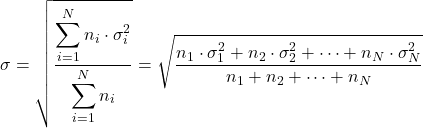Deviasi standar (atau deviasi standar)

Oleh Benjamin anderson Agustus 5, 2023 Statistik 0 Komentar

Artikel ini menjelaskan apa itu simpangan baku, disebut juga simpangan baku. Anda akan mempelajari cara menghitung simpangan baku, contoh praktis langkah demi langkah, dan kalkulator online untuk mencari simpangan baku dari sampel data apa pun.

Berapa simpangan baku (atau simpangan baku)?

Deviasi standar , juga disebut deviasi standar , adalah ukuran penyebaran statistik. Dengan kata lain, standar deviasi adalah nilai yang menunjukkan sebaran sekumpulan data statistik.

Oleh karena itu, simpangan baku (atau simpangan baku) digunakan untuk mengukur penyebaran suatu populasi atau sampel statistik. Semakin besar simpangan baku suatu rangkaian data, maka semakin tersebar data tersebut. Dan interpretasinya juga bisa dilakukan ke arah lain, jika standar deviasinya rendah berarti secara umum datanya sangat mendekati meannya.

Saat menghitung standar deviasi atau deviasi tipikal pada suatu populasi, simbol deviasi standar adalah huruf Yunani sigma (σ). Namun jika menyangkut deviasi standar sampel, huruf s digunakan untuk mewakili pengukuran statistik.

Dalam beberapa buku statistik dan probabilitas, simpangan baku disebut juga simpangan baku.

Rumus simpangan baku (atau simpangan baku).

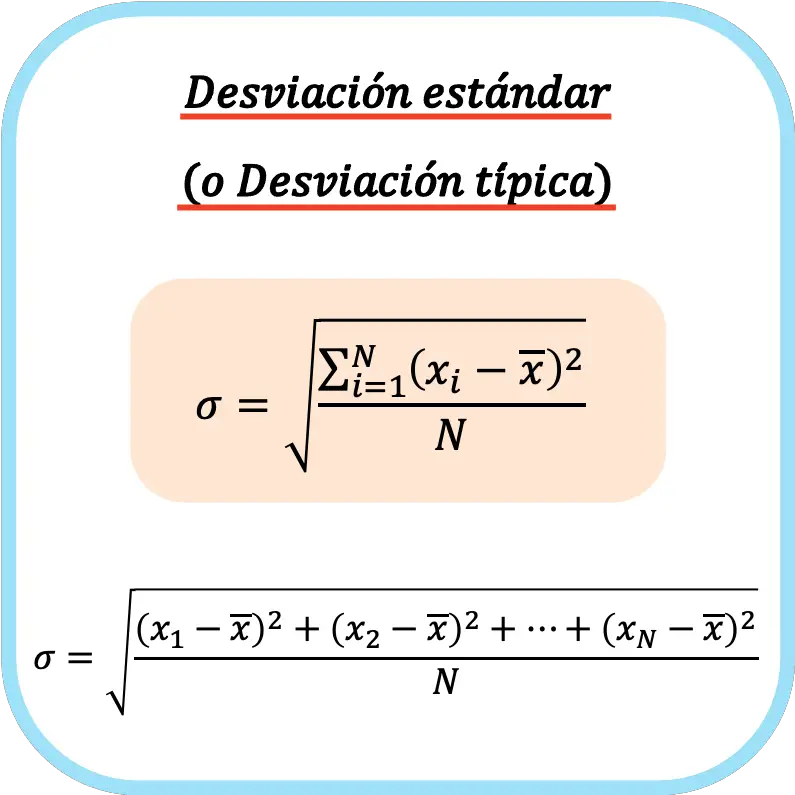
Deviasi standar (atau deviasi standar) sama dengan akar kuadrat dari jumlah kuadrat deviasi rangkaian data dibagi dengan jumlah total observasi.

Oleh karena itu, rumus untuk menghitung simpangan baku (atau simpangan baku) adalah:

👉 Anda dapat menggunakan kalkulator di bawah ini untuk menghitung deviasi standar kumpulan data apa pun.

Kesimpulannya, untuk mencari simpangan baku suatu kumpulan data, Anda perlu menghitung semua simpangan (didefinisikan sebagai selisih antara titik data dan rata-rata aritmatika), tambah simpangannya menjadi dua, jumlahkan semuanya, lalu bagi dengan total. sejumlah data, dan akhirnya mengambil akar kuadrat.

Contoh simpangan baku (atau simpangan baku)

Mengingat definisi deviasi standar (atau deviasi tipikal), di bawah ini adalah contoh langkah demi langkah sehingga Anda dapat melihat bagaimana deviasi standar suatu rangkaian data dihitung.

Hitung simpangan baku dari nilai berikut: 3, 6, 2, 9, 4.

Hal pertama yang perlu kita lakukan adalah menentukan mean sampel. Caranya, kita jumlahkan semua data dan membaginya dengan jumlah observasi, yaitu lima:

$\overline{x}=\cfrac{3+6+2+9+4}{5}=4,8$

Kami sekarang menggunakan rumus deviasi standar:

$\displaystyle\sigma=\sqrt{\frac{\displaystyle\sum_{i=1}^N(x_i-\overline{x})^2}{N}}$

Kami mengganti data ke dalam rumus:

$\displaystyle\sigma =\sqrt{\frac{(3-4,8)^2+(6-4,8)^2+(2-4,8)^2+(9-4,8)^2+(4-4,8)^2}{5}}$

Dan terakhir kita hitung simpangan bakunya:

$\begin{aligned}\displaystyle\sigma & = \sqrt{\frac{(-1,8)^2+1,2^2+(-2,8)^2+4,2^2+(-0,8)^2}{5}}\\[2ex]&=\sqrt{\frac{3,24+1,44+7,84+17,64+0,64}{5}}\\[2ex]&= \sqrt{\frac{30,8}{5}}=\sqrt{6,16}=2,48 \end{aligned}$

Kalkulator Deviasi Standar (atau Deviasi Standar).

Masukkan kumpulan data statistik ke dalam kalkulator online berikut untuk menghitung simpangan baku (atau simpangan baku). Data harus dipisahkan dengan spasi dan dimasukkan menggunakan titik sebagai pemisah desimal.

Deviasi standar (atau tipikal) untuk data yang dikelompokkan

Untuk menghitung simpangan baku (atau simpangan baku) data yang dikelompokkan ke dalam interval , langkah-langkah berikut harus diikuti:

Temukan mean dari data yang dikelompokkan.
Hitung penyimpangan data yang dikelompokkan.
Kuadratkan setiap celah.
Kalikan setiap hasil sebelumnya dengan frekuensi intervalnya.
Tambahkan jumlah semua nilai yang diperoleh pada langkah sebelumnya.
Bagilah dengan jumlah total observasi.
Ambil akar kuadrat dari nilai sebelumnya. Angka yang dihasilkan merupakan simpangan baku dari data yang dikelompokkan.

Kesimpulannya, rumus menghitung simpangan baku data yang dikelompokkan ke dalam interval adalah:

$\displaystyle\sigma=\sqrt{\frac{\displaystyle\sum_{i=1}^N\left(x_i-\overline{x}\right)^2\cdot f_i }{N}}$

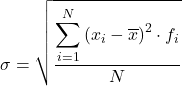
Meskipun rumus di atas biasanya digunakan, ekspresi aljabar berikut juga dapat digunakan karena diperoleh hasil yang sama:

$\displaystyle\sigma=\sqrt{\frac{\displaystyle\sum_{i=1}^n x_i^2\cdot f_i }{N}-\overline{x}^2}$

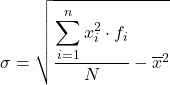
Agar Anda dapat melihat bagaimana hal ini dilakukan, di bawah ini adalah latihan langkah demi langkah tentang deviasi standar data yang dikelompokkan ke dalam interval. Lebih tepatnya, deviasi standar dari data statistik berikut akan dihitung:

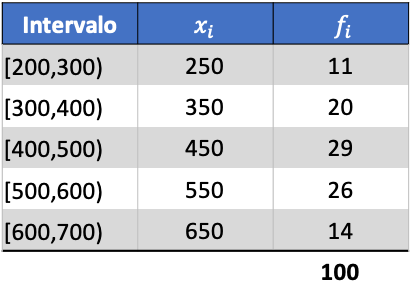
contoh data yang dikelompokkan ke dalam interval

Pertama, kita mengalikan skor kelas setiap interval dengan frekuensinya untuk menghitung mean aritmatika:

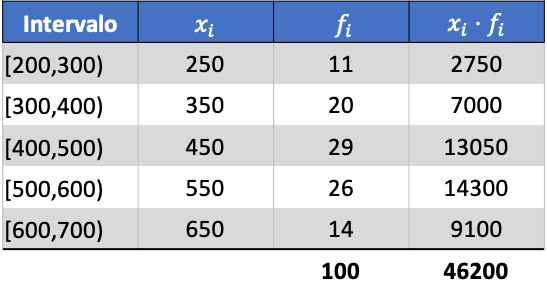
Jadi rata-rata data yang dikelompokkan adalah:

$\overline{x}=\cfrac{\displaystyle\sum_{i=1}^n x_i\cdot f_i}{N}=\cfrac{46200}{100}=462$

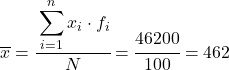
Sekarang kita mengetahui nilai rata-ratanya, kita perlu menambahkan tiga kolom berikut ke tabel data:

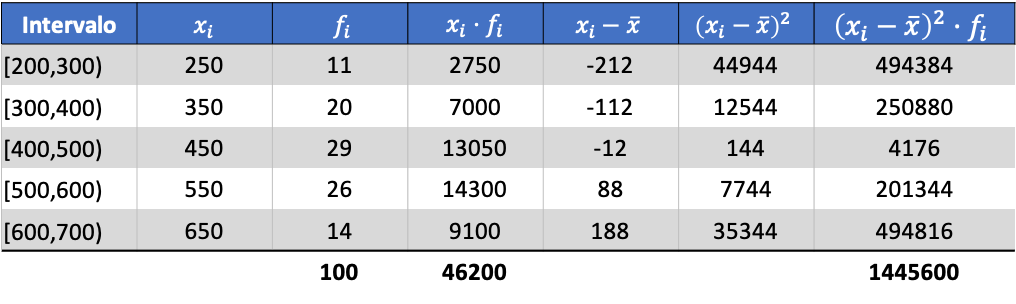
menyelesaikan latihan simpangan baku atau simpangan baku untuk data yang dikelompokkan

Maka simpangan baku data yang dikelompokkan adalah hasil akar kuadrat dari total kolom terakhir dibagi dengan jumlah observasi:

$\displaystyle\sigma=\sqrt{\frac{\displaystyle\sum_{i=1}^N\left(x_i-\overline{x}\right)^2\cdot f_i }{N}}=\sqrt{\frac{1445600}{100}}=120,23$

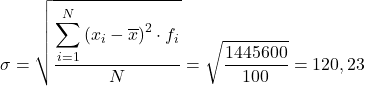
Deviasi dan varians standar (atau tipikal).

Hubungan antara deviasi standar (atau deviasi tipikal) dan varians adalah deviasi standar adalah akar kuadrat dari varians.

Jadi, jika kita mengetahui nilai varians suatu kumpulan data, kita dapat dengan mudah menghitung simpangan baku dengan mengambil akar kuadrat. Atau sebaliknya, jika kita mengetahui simpangan baku, kita dapat mencari variansnya dengan mengkuadratkan nilainya.

$Var(X)=\sigma^2$

Faktanya, varians dapat direpresentasikan hanya dengan menggunakan simbol deviasi standar kuadrat. Oleh karena itu, simbol varians populasi adalah sigma kuadrat (σ ² ) dan simbol varians sampel adalah s kuadrat (s ² ).

Selain itu, konsep deviasi standar dan varians memiliki interpretasi yang serupa, karena keduanya menunjukkan penyebaran serangkaian data statistik.

Sifat simpangan baku (atau simpangan baku)

Simpangan baku mempunyai sifat sebagai berikut:

Deviasi standar sampel data tidak boleh negatif.

$\sigma \ge 0$

Simpangan baku akan menjadi nol jika semua datanya sama.

$\sigma =0$

Jika suatu suku konstanta ditambahkan pada semua data, maka nilai deviasi standarnya tidak berubah.

$\sigma (X+k)=\sigma (X)$

Jika seluruh data dikalikan dengan suatu angka, maka simpangan bakunya akan dikalikan dengan nilai absolut dari angka tersebut.

$\sigma (k\cdot X)=|k|\cdot \sigma (X)$

Simpangan baku jumlah dua variabel acak sama dengan akar kuadrat jumlah varians variabel ditambah dua kali kovarians antara kedua variabel.

$\sigma(X+Y)=\sqrt{Var(X)+Var(Y)+2\cdot Cov(X,Y)}$

Jika kita mengetahui simpangan baku dari berbagai distribusi (σ _i ) dan jumlah datanya (n _i ), kita dapat menghitung simpangan baku total dengan menerapkan rumus berikut:

$\displaystyle\sigma=\sqrt{\frac{\displaystyle \sum_{i=1}^N n_i\cdot \sigma_i^2}{\displaystyle \sum_{i=1}^N n_i}}=\sqrt{\frac{\displaystyle n_1\cdot \sigma_1^2+n_2\cdot \sigma_2^2+\dots +n_N\cdot \sigma_N^2}{\displaystyle n_1+n_2+\dots+n_N}}$

Tentang Penulis

Benjamin anderson

Halo, saya Benjamin, pensiunan profesor statistika yang menjadi guru Statorial yang berdedikasi. Dengan pengalaman dan keahlian yang luas di bidang statistika, saya ingin berbagi ilmu untuk memberdayakan mahasiswa melalui Statorials. Baca selengkapnya