Cara menghitung z score di spss
Skor-z memberi tahu kita berapa banyak deviasi standar suatu nilai tertentu dari mean.
Skor-z dari nilai tertentu dihitung sebagai berikut:
skor-z = (x – μ) / σ
Emas:
- x: nilai individu
- μ: rata-rata populasi
- σ: deviasi standar populasi
Tutorial ini menjelaskan cara menghitung z-score di SPSS.
Terkait: Cara Menafsirkan Skor Z
Cara Menghitung Z Score di SPSS
Misalkan kita mempunyai kumpulan data berikut yang menunjukkan pendapatan tahunan (dalam ribuan) dari 15 orang:
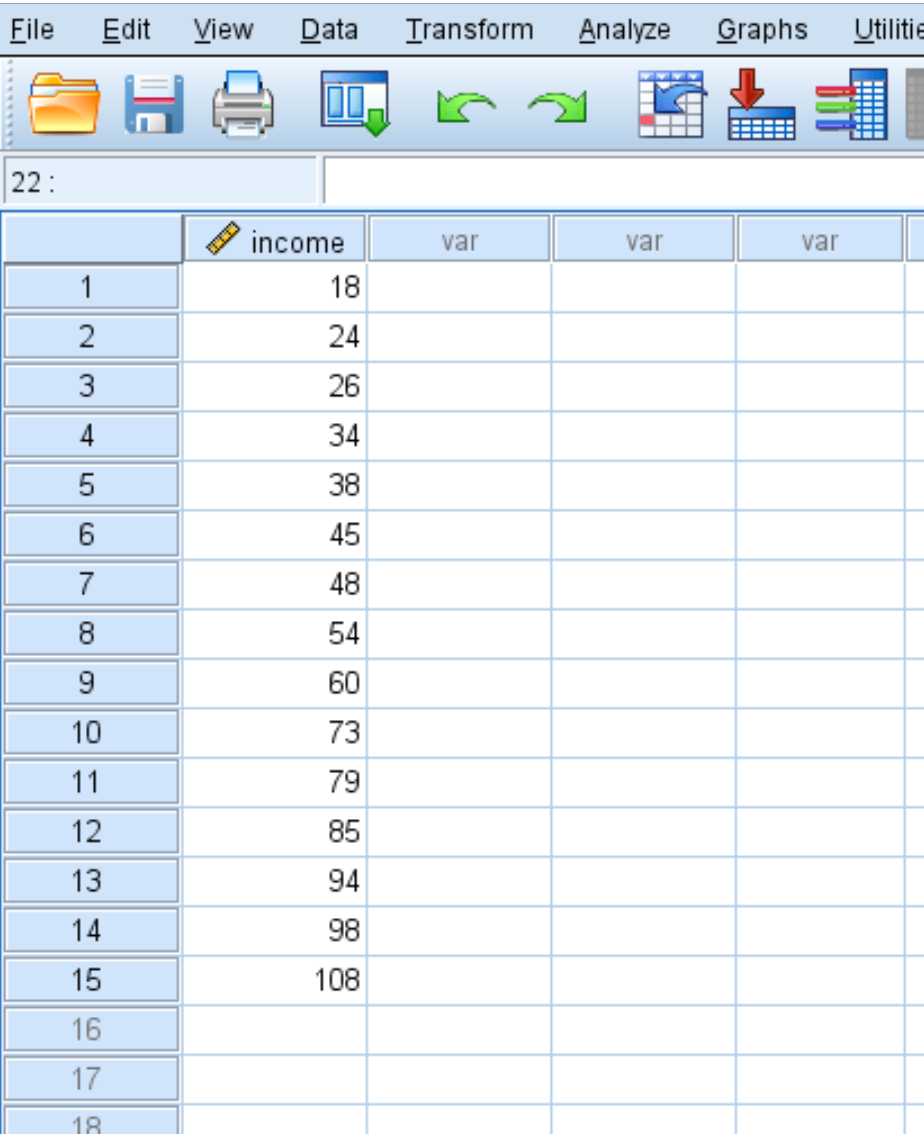
Untuk menghitung skor-z untuk setiap nilai dalam kumpulan data, klik tab Analisis , lalu Statistik Deskriptif , lalu Deskriptif :
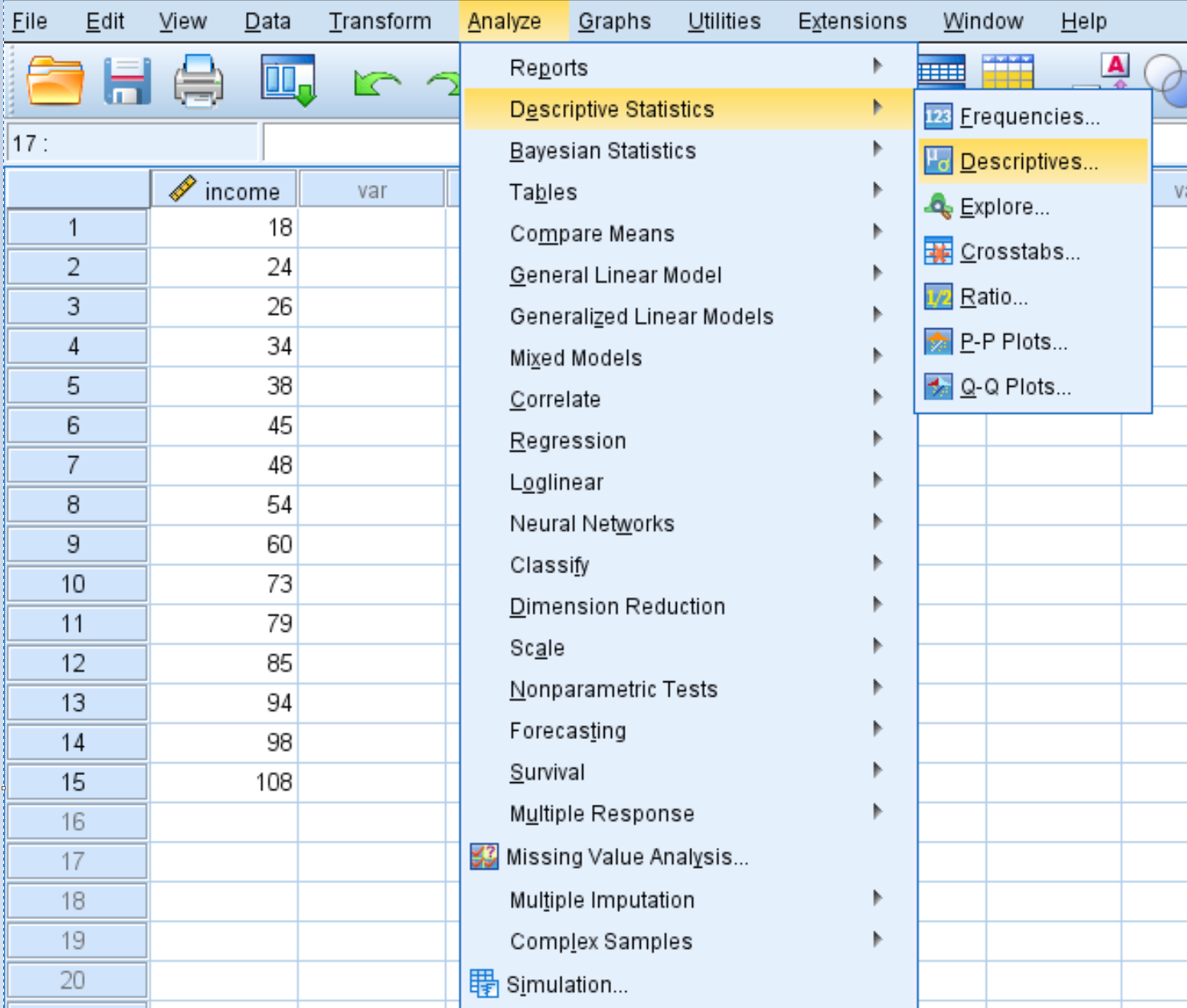
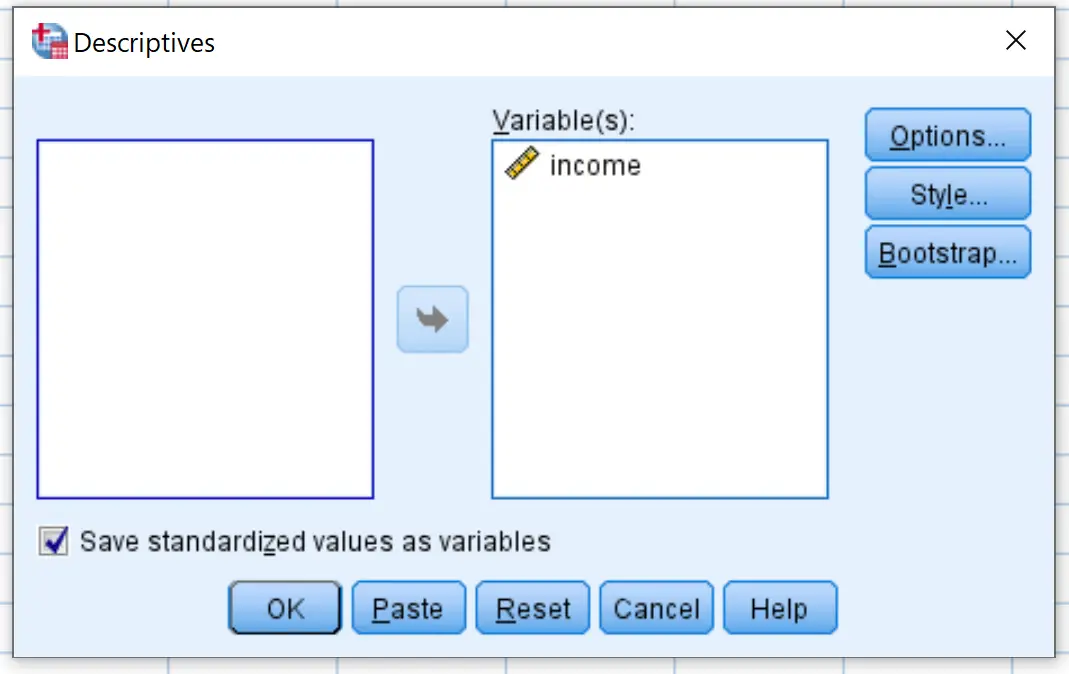
Di jendela baru yang muncul, seret variabel pendapatan ke dalam kotak berlabel Variabel.
Pastikan kotak dicentang di sebelah Simpan nilai standar sebagai variabel , lalu klik OK .
Setelah Anda mengklik OK , SPSS akan menghasilkan tabel statistik deskriptif untuk dataset Anda:
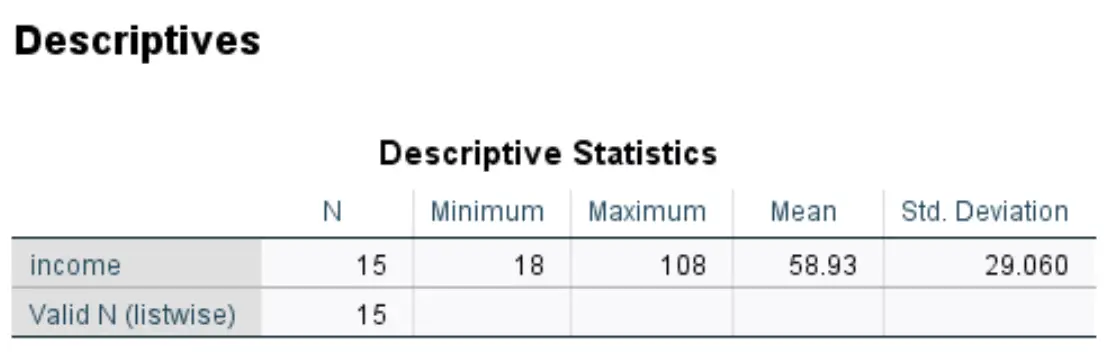
SPSS juga akan menghasilkan kolom nilai baru yang menampilkan z-score untuk setiap nilai asli pada dataset Anda:
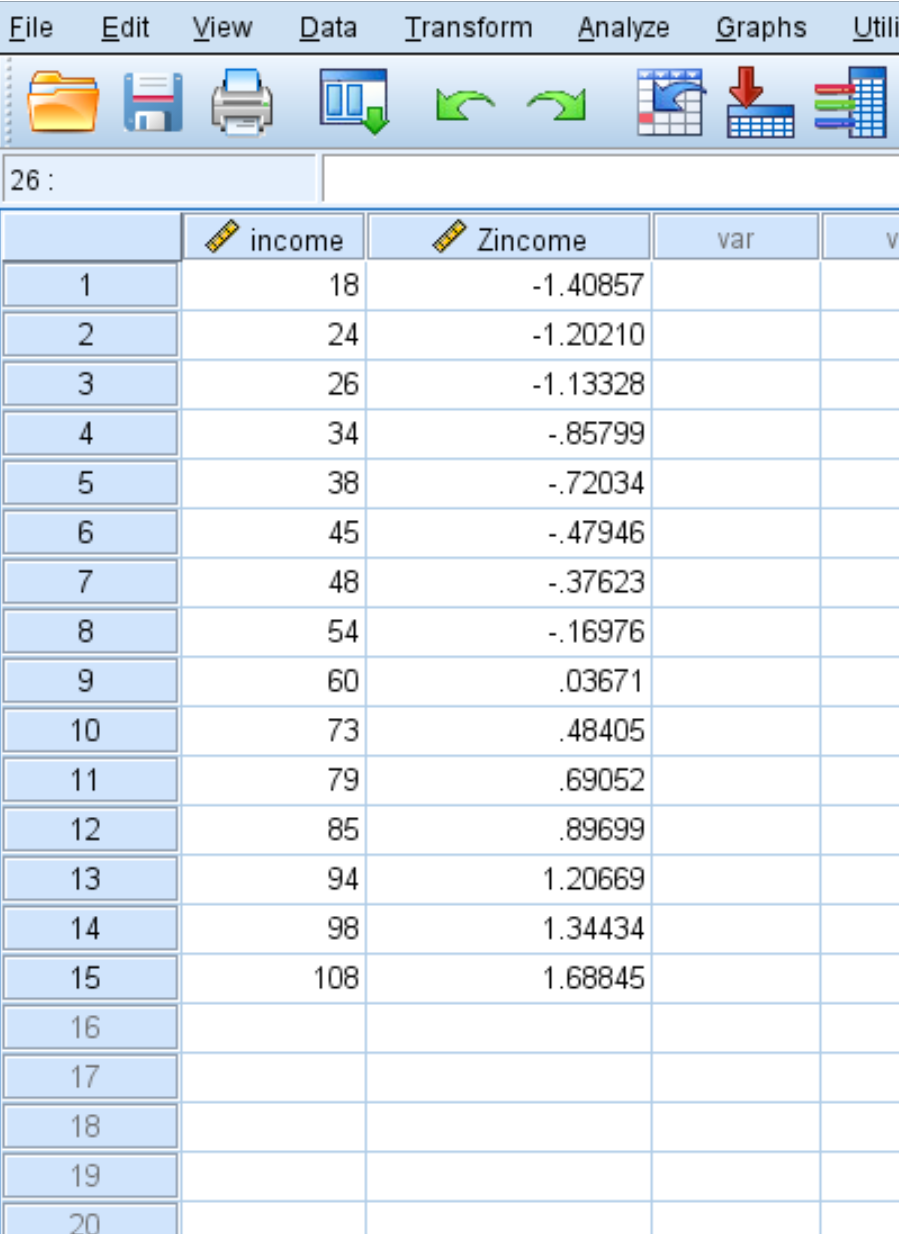
Masing-masing skor z dihitung menggunakan rumus z = (x – μ) / σ
Misalnya z-score untuk nilai pendapatan 18 adalah:
z = (18 – 58,93) / 29,060 = -1,40857 .
Skor Z untuk semua nilai data lainnya dihitung dengan cara yang sama.
Bagaimana menafsirkan skor Z
Ingatlah bahwa skor-z hanya memberi tahu kita berapa banyak deviasi standar suatu nilai dari mean.
Skor z bisa positif, negatif, atau sama dengan nol:
- Skor z yang positif menunjukkan bahwa suatu nilai tertentu berada di atas rata-rata.
- Skor z negatif menunjukkan bahwa nilai tertentu berada di bawah rata-rata.
- Skor z nol menunjukkan bahwa nilai tertentu sama dengan mean.
Dalam contoh kita, kita menemukan bahwa rata-ratanya adalah 58,93 dan deviasi standarnya adalah 29,060.
Jadi, nilai pertama pada dataset kita adalah 18, yang memiliki z-score (18 – 58.93) / 29.060 = -1.40857 .
Artinya nilai “18” adalah 1,40857 standar deviasi lebih rendah dari mean.
Sebaliknya, nilai terakhir dalam data kami adalah 108, yang setara dengan skor-z (108 – 58,93) / 29,060 = 1,68845 .
Artinya nilai “108” berada di atas standar deviasi 1,68845 mean.
Sumber daya tambahan
Tutorial berikut menjelaskan cara melakukan tugas umum lainnya di SPSS:
Cara menghitung statistik deskriptif variabel di SPSS
Cara menghitung ringkasan lima digit di SPSS
Cara mengidentifikasi outlier di SPSS