Cara menggunakan distribusi binomial dengan python

Distribusi binomial adalah salah satu distribusi yang paling umum digunakan dalam statistik. Ini menggambarkan probabilitas memperoleh k keberhasilan dalam n percobaan binomial.

Jika suatu variabel acak X mengikuti distribusi binomial, maka peluang keberhasilan X = k dapat dicari dengan rumus berikut:

P(X=k) = _n C _k * p ^k * (1-p) ^nk

Emas:

• n: jumlah percobaan
• k: jumlah keberhasilan
• p: probabilitas keberhasilan pada percobaan tertentu
• _n C _k : banyaknya cara untuk memperoleh k keberhasilan dalam n percobaan

Tutorial ini menjelaskan cara menggunakan distribusi binomial dengan Python.

Cara menghasilkan distribusi binomial

Anda dapat menghasilkan array nilai yang mengikuti distribusi binomial menggunakan fungsi random.binomial perpustakaan numpy:

 from numpy import random

#generate an array of 10 values that follows a binomial distribution
random.binomial(n=10, p=.25, size=10)

array([5, 2, 1, 3, 3, 3, 2, 2, 1, 4])

Setiap angka dalam tabel yang dihasilkan mewakili jumlah “keberhasilan” yang ditemui selama 10 percobaan dengan probabilitas keberhasilan dalam percobaan tertentu adalah 0,25 .

Cara menghitung probabilitas menggunakan distribusi binomial

Anda juga dapat menjawab pertanyaan tentang probabilitas binomial menggunakan fungsi binom perpustakaan scipy.

Pertanyaan 1: Nathan melakukan 60% percobaan lemparan bebasnya. Jika dia melakukan 12 lemparan bebas, berapakah peluang dia berhasil tepat 10 lemparan bebas?

 from scipy.stats import binom

#calculate binomial probability
binom.pmf(k= 10 , n= 12 , p= 0.6 )

0.0639

Peluang Nathan melakukan tepat 10 lemparan bebas adalah 0,0639 .

Pertanyaan 2: Marty melempar koin sebanyak 5 kali. Berapa peluang munculnya koin tersebut sebanyak 2 kali atau kurang?

 from scipy.stats import binom

#calculate binomial probability
binom.cdf(k= 2 , n= 5 , p= 0.5 )

0.5

Peluang munculnya koin 2 kali atau kurang adalah 0,5 .

Pertanyaan 3: Kita tahu bahwa 70% orang mendukung undang-undang tertentu. Jika 10 orang dipilih secara acak, berapa peluang terambilnya antara 4 dan 6 orang yang mendukung undang-undang tersebut?

 from scipy.stats import binom

#calculate binomial probability
binom.cdf(k= 6 , n= 10 , p= 0.7 ) - binom.cdf(k= 3 , n= 10 , p= 0.7 )

0.3398

Peluang antara 4 dan 6 orang yang dipilih secara acak mendukung hukum adalah 0,3398 .

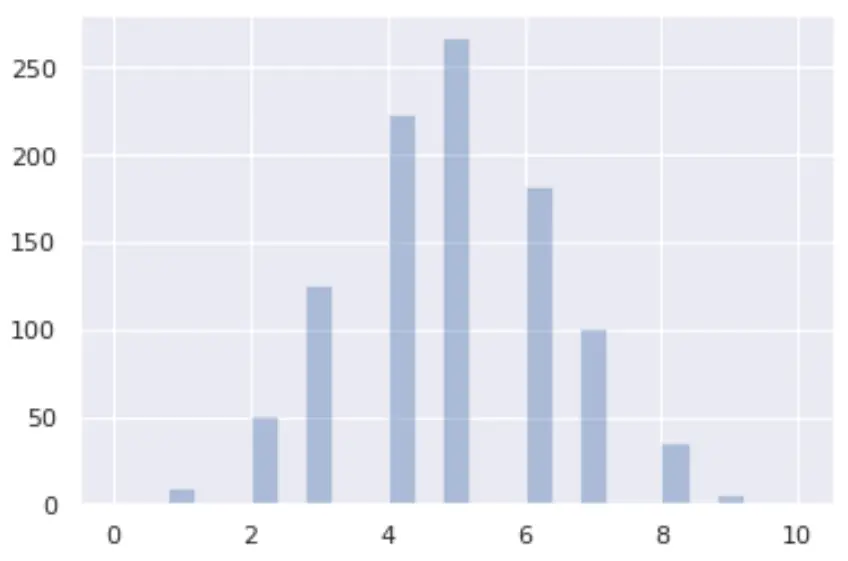
Bagaimana memvisualisasikan distribusi binomial

Anda dapat memvisualisasikan distribusi binomial dengan Python menggunakan pustaka seaborn dan matplotlib :

 from numpy import random
import matplotlib.pyplot as plt
import seaborn as sns

x = random.binomial(n= 10 , p= 0.5 , size= 1000 )

sns.distplot(x, hist= True , kde= False )

plt.show()

teh