Matriks korelasi

Oleh Benjamin anderson Agustus 5, 2023 Statistik 0 Komentar

Pada artikel ini Anda akan mengetahui apa itu matriks korelasi, apa rumusnya, dan bagaimana menafsirkan matriks korelasi. Selain itu, Anda akan dapat melihat contoh nyata interpretasi matriks korelasi.

Apa itu matriks korelasi?

Matriks korelasi adalah matriks yang pada posisi i,j memuat koefisien korelasi antara variabel i dan j .

Oleh karena itu, matriks korelasi adalah matriks persegi yang diisi dengan matriks pada diagonal utama dan elemen baris i dan kolom j terdiri dari nilai koefisien korelasi antara variabel i dan variabel j .

Oleh karena itu, rumus matriks korelasinya adalah sebagai berikut:

Emas

$r_{ij}$

adalah koefisien korelasi antar variabel

$i$

Dan

$j.$

Jadi, untuk menemukan matriks korelasi suatu kumpulan data, penting bagi Anda untuk mengetahui cara menghitung koefisien korelasi. Jika Anda tidak ingat, di tautan berikut Anda akan mengetahui cara melakukannya dengan kalkulator online:

➤ Lihat: kalkulator koefisien korelasi

Sifat koefisien korelasi adalah urutan variabel tidak menjadi masalah dalam perhitungannya, yaitu koefisien korelasi

$r_{ij}$

setara dengan

$r_{ji}.$

Oleh karena itu, matriks korelasinya simetris.

$\displaystyle R=\begin{pmatrix}1&r_{12}&r_{13}&\dots&r_{1n}\\[1.1ex] r_{12}&1&r_{23}&\dots&r_{2n}\\[1.1ex] r_{13}&r_{23}&1&\dots&r_{3n}\\[1.1ex] \vdots &\vdots &\vdots &\ddots &\vdots\\[1.1ex] r_{1n}&r_{2n}&r_{3n}&\dots&1\end{pmatrix}$

Agar matriks korelasi bermakna, kumpulan data statistik harus memiliki lebih dari dua variabel. Jika tidak, cukup menentukan koefisien korelasi tunggal dan matriks korelasi akan bermakna.

Cara membuat matriks korelasi

Mengingat definisi matriks korelasi, mari kita lihat bagaimana matriks statistik jenis ini dibuat:

Hitung koefisien korelasi setiap pasangan variabel. Perhatikan bahwa urutan variabel tidak mengubah hasilnya, sehingga hanya perlu dihitung satu kali untuk setiap pasangan variabel.
Buat matriks persegi yang dimensinya sama dengan jumlah variabel dalam deret data. Matriks ini akan menjadi matriks korelasi.
Beri tanda 1 pada setiap elemen diagonal utama matriks korelasi.
Letakkan koefisien korelasi variabel i , j pada posisi i , j dan j , i .
Setelah matriks korelasi dibuat, yang tersisa hanyalah menafsirkan nilai-nilainya.

Ingatlah bahwa menjalankan matriks korelasi saja tidak cukup, Anda perlu menafsirkan nilainya dan memahami artinya. Bagian berikut menjelaskan cara menafsirkan matriks korelasi.

Interpretasi matriks korelasi

Untuk menafsirkan matriks korelasi dengan benar, perlu diperhatikan bahwa nilai koefisien korelasi dapat berkisar dari -1 hingga +1:

r=-1 : kedua variabel mempunyai korelasi negatif sempurna, sehingga kita dapat menarik garis dengan kemiringan negatif yang menghubungkan semua titik.
-1<r<0 : korelasi kedua variabel bernilai negatif, sehingga jika salah satu variabel meningkat maka variabel lainnya menurun. Semakin dekat nilainya dengan -1, maka variabel-variabel tersebut mempunyai hubungan yang semakin negatif.
r=0 : korelasi kedua variabel sangat lemah, bahkan hubungan linier keduanya adalah nol. Hal ini tidak berarti bahwa variabel-variabel tersebut independen, karena bisa saja mempunyai hubungan non-linier.
0<r<1 : korelasi kedua variabel bernilai positif, semakin mendekati +1 maka semakin kuat hubungan antar variabel. Dalam hal ini, satu variabel cenderung meningkat nilainya ketika variabel lainnya juga meningkat.
r=1 : kedua variabel mempunyai korelasi positif sempurna, yaitu mempunyai hubungan linier positif.

Oleh karena itu, untuk menginterpretasikan matriks korelasi, perlu menginterpretasikan setiap koefisien korelasi dan membandingkan hasil yang berbeda.

Dengan cara ini Anda akan dapat melihat variabel mana yang paling berhubungan satu sama lain, variabel mana yang paling penting, variabel mana yang praktis tidak ada hubungan satu sama lain, dan seterusnya.

Contoh Matriks Korelasi

Untuk memahami sepenuhnya apa itu matriks korelasi dan bagaimana interpretasinya, pada bagian ini kita akan menganalisis contoh matriks korelasi:

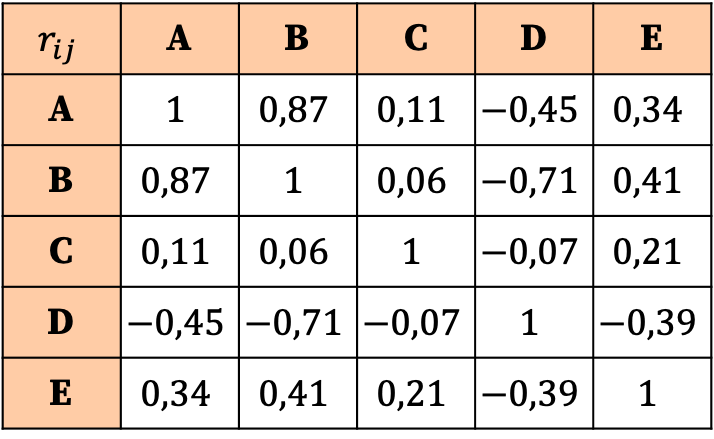
Interpretasi matriks korelasi didasarkan pada nilai koefisien. Dengan demikian, kita dapat melihat bahwa korelasi yang paling kuat adalah hubungan antara variabel A dan variabel B, karena koefisien korespondennya adalah yang terbesar (0,87).

Di sisi lain, variabel C praktis tidak memiliki korelasi dengan variabel apa pun, karena semua koefisiennya sangat mendekati nol sehingga sangat rendah. Oleh karena itu, untuk menyederhanakan analisis, kami bahkan dapat mempertimbangkan untuk menghapus variabel ini dari studi statistik.

Begitu pula seluruh hubungan variabel D dengan variabel lainnya adalah negatif, artinya korelasi antara variabel D dengan variabel lain berbanding terbalik. Hal ini tidak berarti bahwa variabel tersebut harus dihilangkan, hanya saja variabel D berkorelasi negatif.

Seperti yang Anda lihat, matriks korelasi sangat berguna untuk merangkum data dan membuat analisis keseluruhan tentang hubungan antara berbagai variabel dalam kumpulan data.

Tentang Penulis

Benjamin anderson

Halo, saya Benjamin, pensiunan profesor statistika yang menjadi guru Statorial yang berdedikasi. Dengan pengalaman dan keahlian yang luas di bidang statistika, saya ingin berbagi ilmu untuk memberdayakan mahasiswa melalui Statorials. Baca selengkapnya