Cara membuat plot sisa dengan python
Plot sisa adalah jenis plot yang menampilkan nilai yang sesuai dengan sisa model regresi .
Jenis plot ini sering digunakan untuk mengevaluasi apakah model regresi linier sesuai atau tidak untuk kumpulan data tertentu dan untuk memeriksa residu untuk heteroskedastisitas .
Tutorial ini menjelaskan cara membuat plot sisa untuk model regresi linier dengan Python.
Contoh: plot sisa dengan Python
Untuk contoh ini, kita akan menggunakan kumpulan data yang mendeskripsikan atribut 10 pemain bola basket:
import numpy as np import pandas as pd #create dataset df = pd.DataFrame({'rating': [90, 85, 82, 88, 94, 90, 76, 75, 87, 86], 'points': [25, 20, 14, 16, 27, 20, 12, 15, 14, 19], 'assists': [5, 7, 7, 8, 5, 7, 6, 9, 9, 5], 'rebounds': [11, 8, 10, 6, 6, 9, 6, 10, 10, 7]}) #view dataset df rating points assists rebounds 0 90 25 5 11 1 85 20 7 8 2 82 14 7 10 3 88 16 8 6 4 94 27 5 6 5 90 20 7 9 6 76 12 6 6 7 75 15 9 10 8 87 14 9 10 9 86 19 5 7
Plot sisa untuk regresi linier sederhana
Misalkan kita memasang model regresi linier sederhana dengan menggunakan poin sebagai variabel prediktor dan nilai sebagai variabel respon:
#import necessary libraries import matplotlib.pyplot as plt import statsmodels.api as sm from statsmodels.formula.api import ols #fit simple linear regression model model = ols('rating ~ points', data=df). fit () #view model summary print(model.summary())
Kita dapat membuat plot sisa atau plot pas menggunakan fungsi plot_regress_exog() dari perpustakaan statsmodels:
#define figure size fig = plt.figure(figsize=(12,8)) #produce regression plots fig = sm.graphics.plot_regress_exog(model, ' points ', fig=fig)
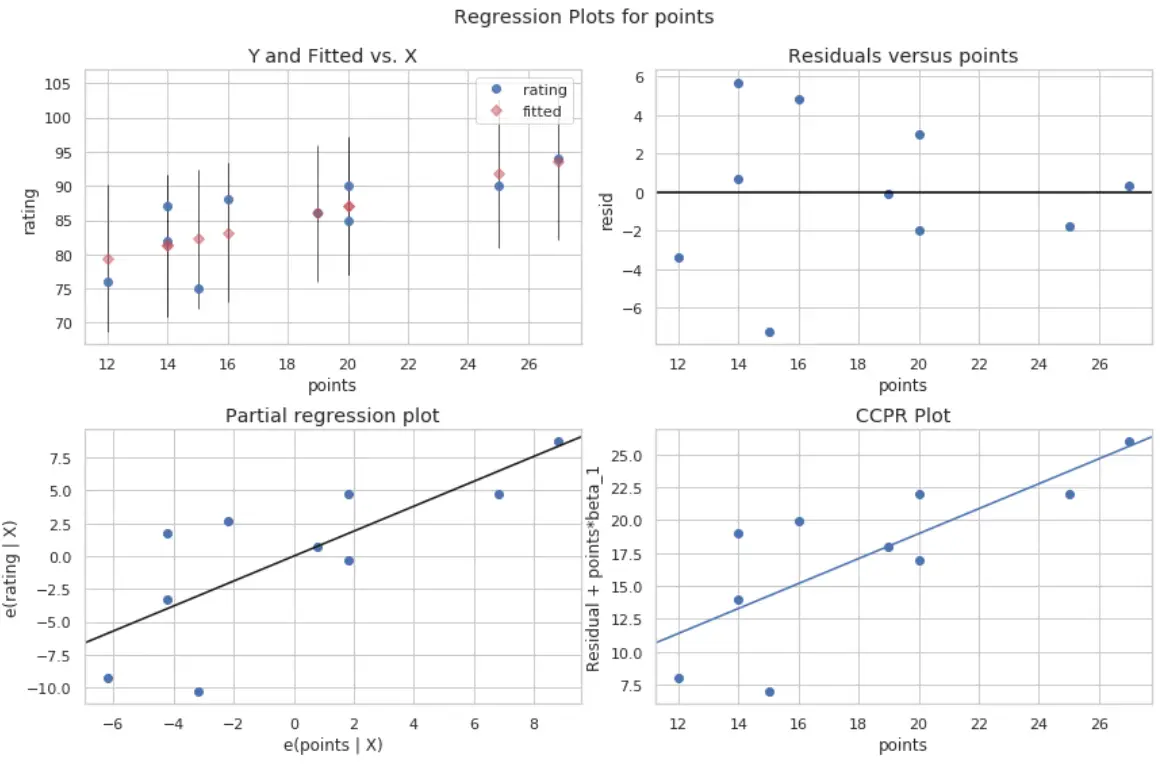
Empat plot diproduksi. Yang di pojok kanan atas adalah plot sisa versus plot yang disesuaikan. Sumbu x pada plot ini menunjukkan nilai sebenarnya dari titik variabel prediktor dan sumbu y menunjukkan sisa nilai tersebut.
Karena residu tampak tersebar secara acak di sekitar nol, hal ini menunjukkan bahwa heteroskedastisitas tidak menjadi masalah pada variabel prediktor.
Plot sisa untuk regresi linier berganda
Misalkan kita menyesuaikan model regresi linier berganda dengan menggunakan assist dan rebound sebagai variabel prediktor dan rating sebagai variabel respons:
#fit multiple linear regression model model = ols('rating ~ assists + rebounds', data=df). fit () #view model summary print(model.summary())
Sekali lagi, kita dapat membuat plot sisa versus prediktor untuk masing-masing prediktor menggunakan fungsi plot_regress_exog() dari perpustakaan statsmodels.
Misalnya, seperti inilah plot sisa/prediktor untuk bantuan variabel prediktor :
#create residual vs. predictor plot for 'assists' fig = plt.figure(figsize=(12,8)) fig = sm.graphics.plot_regress_exog(model, ' assists ', fig=fig)
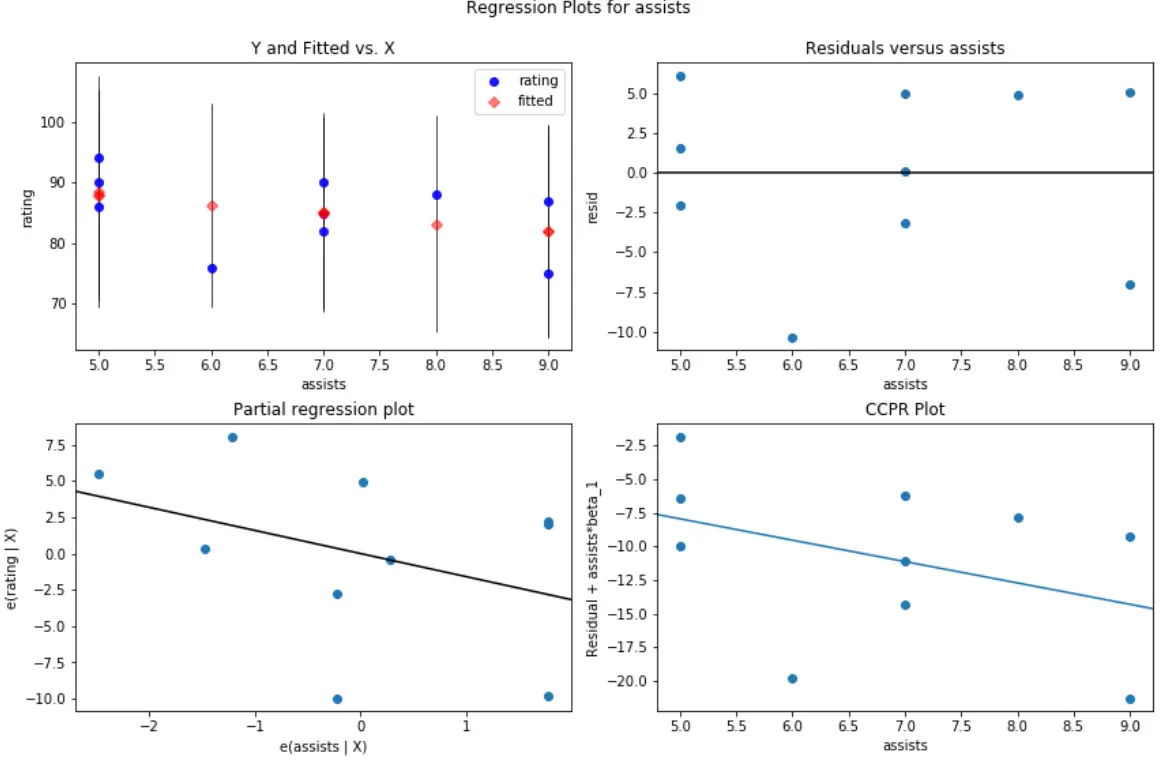
Dan seperti inilah plot sisa/prediktor untuk pantulan variabel prediktor :
#create residual vs. predictor plot for 'assists' fig = plt.figure(figsize=(12,8)) fig = sm.graphics.plot_regress_exog(model, ' rebounds ', fig=fig)
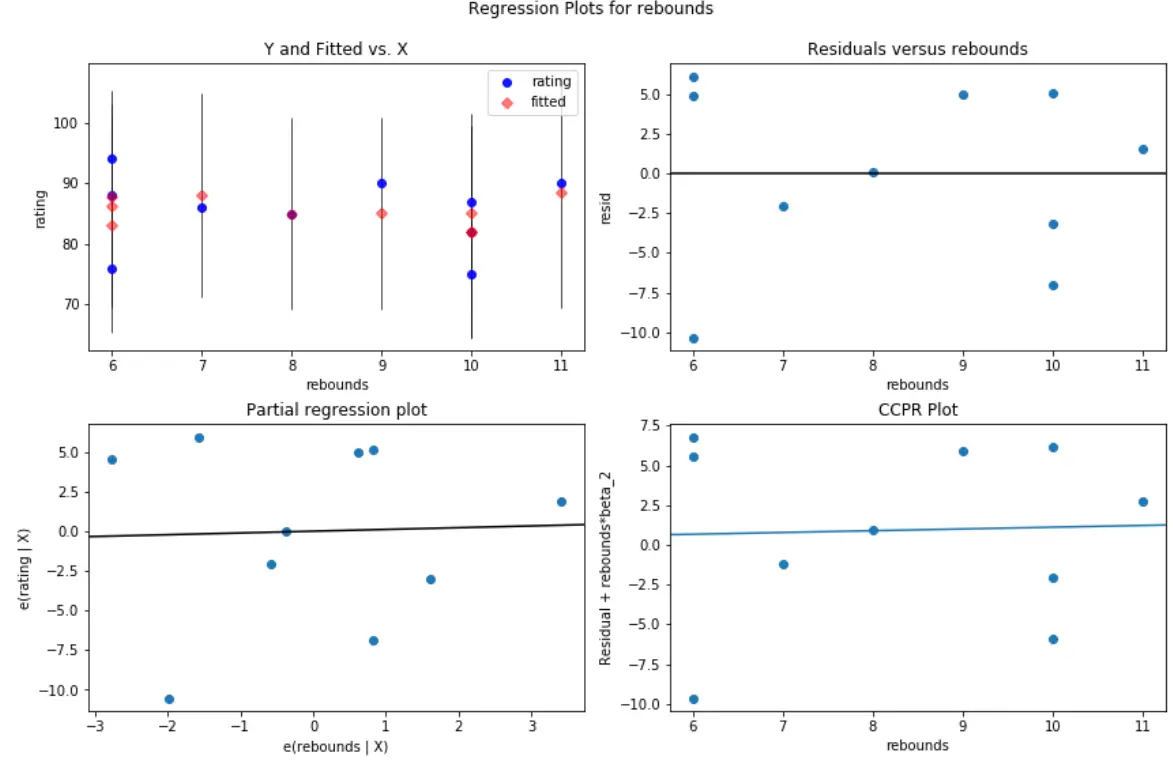
Pada kedua plot, residu tampak tersebar secara acak di sekitar nol, menunjukkan bahwa heteroskedastisitas tidak menjadi masalah pada variabel prediktor mana pun dalam model.